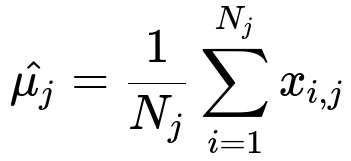ML Interview Q Series: How do you cope with Missing data in Regression?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

One of the most common challenges in regression is how to handle missing data. Failing to deal properly with missing values can introduce bias or reduce the accuracy of your predictive model. There are various strategies, each with its own strengths and weaknesses.

Deletion-Based Methods

A frequent initial approach involves removing any rows or columns that contain missing values. If the fraction of missing data is small and randomly distributed, this can be an acceptable option. However, when the missingness is prevalent or not random, simple deletion can bias the model or discard important information.

Simple Imputation

Simple imputation usually replaces the missing values with summary statistics of the available data. For numerical features, one might replace missing entries with the feature’s mean, median, or mode (for categorical features). Although straightforward, simple imputation can introduce bias because it does not reflect the inherent uncertainty about the missing value.

Below is the primary formula to compute the mean for a single feature j, which is then used to fill any missing values in that feature column:

Here, x_{i, j} is the i-th observed value for feature j, and N_j is the total count of non-missing observations in feature j.

In this formula, once the mean is calculated, any missing entry in the j-th column can be replaced with this computed mean. While this is easy to implement, it does not account for correlations with other features, nor does it reflect the variability of the data (all missing points get the same imputed value).

Imputation Using Models

One can build a predictive model to estimate missing values. For instance, you can predict the missing values in a particular feature using the other features as inputs. Variations include k-Nearest Neighbors (kNN) imputation, regression-based imputation, or iterative approaches such as Multivariate Imputation by Chained Equations (MICE). These methods tend to be more sophisticated and can preserve relationships among features.

kNN imputation, for example, finds the k closest samples with respect to some distance metric (like Euclidean distance) among the rows that do not have a missing value in that particular feature. The missing value is then replaced by the average of these neighbors. This preserves local structure but can be slow when the dataset is large. Iterative methods like MICE repeatedly model each feature with missing entries as a function of other features until convergence.

Multiple Imputation

Multiple imputation creates several different imputed datasets, each with plausible values for the missing data. You then train your model on each of these datasets and pool the results. This process acknowledges the inherent uncertainty in the missing values by allowing them to vary. Typically, the final model’s parameters (for example, coefficients in a linear regression) are aggregated using a method such as Rubin’s rules to combine estimates from each imputed dataset. Multiple imputation is a robust approach because it accounts for variability in the imputed values, although it is more computationally intensive.

Using Algorithms That Handle Missing Data Natively

Certain tree-based methods, like some implementations of Random Forests or Gradient Boosted Trees, can accommodate missing data by effectively learning default splitting directions for missing values. While not universal in all implementations, these techniques reduce the need for explicit imputation, though they may internally learn separate paths for missing vs. non-missing data. When used appropriately, these methods can handle complex patterns of missingness without heavy feature-engineering overhead.

Practical Implementation Example in Python

Below is a short code snippet showing how to handle missing data in a regression pipeline using scikit-learn’s SimpleImputer. This example demonstrates how you might chain preprocessing steps with a regression model:

import numpy as np
import pandas as pd
from sklearn.impute import SimpleImputer
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split

# Sample data
df = pd.DataFrame({
    'feature1': [1.2, 2.5, np.nan, 4.1, 5.7],
    'feature2': [3.4, np.nan, 6.2, 8.1, 9.0],
    'target': [10, 14, 20, 22, 28]
})

X = df[['feature1', 'feature2']]
y = df['target']

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

# Pipeline with imputation + linear regression
pipeline = Pipeline([
    ('imputer', SimpleImputer(strategy='mean')),
    ('regressor', LinearRegression())
])

pipeline.fit(X_train, y_train)
predictions = pipeline.predict(X_test)
print("Predictions:", predictions)

In this pipeline, each missing value in feature1 or feature2 is replaced by the respective column mean. Other more advanced imputers (like IterativeImputer) can be substituted for improved performance if the missingness structure is more complex.

Considerations and Challenges

It is vital to analyze the nature of missingness. If data is Missing Completely at Random (MCAR), simpler methods like mean imputation or pairwise deletion can be sufficient. If data is Missing at Random (MAR) or Missing Not at Random (MNAR), you may need more advanced techniques, as naive approaches can bias your parameter estimates. Multiple imputation or model-based imputation methods are often better when the missingness is not purely random, or you suspect relationships among features or with the target that might inform the missing data.

Follow-Up Questions

What is the difference between MCAR, MAR, and MNAR?

MCAR (Missing Completely at Random) means the probability of a value being missing does not depend on observed or unobserved variables. In other words, missingness is effectively random. MAR (Missing at Random) means the missingness can be explained by observed data but not by the unobserved variable itself. MNAR (Missing Not at Random) implies there is a systematic reason for the missingness that depends on the unobserved value itself.

When data is MCAR, deletion or simple imputation generally does not bias your model too much. MAR can often be addressed by multiple imputation, because you can use the relationship among observed features to predict the missing ones. MNAR is the hardest to handle because you need to model why the data is missing, often requiring domain knowledge or advanced modeling to account for the missingness mechanism directly.

When should we use multiple imputation over simple imputation?

Multiple imputation is especially useful if there is moderate to substantial missing data and you have reason to believe your missing data mechanism is MAR rather than MCAR. Simple imputation (like mean replacement) does not capture the uncertainty associated with missingness—it replaces all missing values with a single best guess. Multiple imputation, on the other hand, creates multiple plausible versions of your dataset to reflect the uncertainty in the missing values, then combines results to reduce bias and account for the variability across those imputed datasets. This is more computationally intensive but generally leads to more reliable estimates, particularly for inference tasks.

How can kNN imputation bias the regression results?

kNN imputation can introduce bias if your chosen k or distance metric does not align well with the true data structure. For example, if you select too small a k, the imputations might be heavily influenced by outliers or unrepresentative neighbors. If k is too large, imputed values could be overly averaged and lose important nuances. Furthermore, if your data contains many correlated features or very high dimensionality, distances between points might become less meaningful (the curse of dimensionality), which can degrade the performance of kNN imputation.

Does deletion-based approach ever remain a good strategy?

Deletion-based approaches (listwise or pairwise deletion) remain viable if you have a large dataset where only a small fraction of observations are missing, especially if the data can be reasonably assumed to be MCAR. In that scenario, the removed observations are unlikely to distort the distribution significantly. However, if the missingness is systematic or if you lose a large portion of your data by deleting rows/columns, this approach can severely limit your statistical power and inject bias.

How do tree-based algorithms handle missing values?

Some implementations of tree-based methods, such as certain versions of XGBoost or lightGBM, can handle missing values by learning the best direction (left or right branch) to send missing data during the training phase. This approach effectively learns a unique split rule for missing values at each node, allowing the model to account for the possibility that the missingness itself carries information. While this approach can be powerful, the exact treatment of missing values can differ among implementations, and it is essential to ensure the chosen library or framework truly supports this feature.

What are the edge cases when the majority of data is missing?

When the majority of your features or rows are missing, even sophisticated imputation methods might fail. In such cases, the confidence intervals around your imputed values grow very large, and the model might not converge to anything meaningful. You may need to:

• Collect more data if possible.

• Discard features or samples that have too many missing values, but only if justified.

• Apply domain-specific knowledge or external data sources to guide the imputation process.

In these extreme situations, advanced methods like multiple imputation or specialized Bayesian approaches might still be attempted, but interpretability and reliability can be limited.

Why might multiple imputation be costly, and how to handle the computation overhead?

Multiple imputation requires generating multiple imputed datasets (often five to ten). Each dataset must be processed or modeled separately, and then the results are pooled. This repetition increases computational costs, especially for large datasets or complex models. Distributed computing resources or efficient libraries that implement parallelized imputation can mitigate this overhead. You can also reduce the number of imputations if the dataset is massive, though that might slightly increase the variance of the final estimates.

When making the decision, weigh the computational cost against the benefit of more accurate and less biased parameter estimates. In critical applications (e.g., medical statistics, finance), the extra overhead is usually justified to improve model reliability.

Below are additional follow-up questions

How do we handle missing values when they occur in the target variable for a regression problem?

When the target variable itself has missing values, you lose direct supervision for those examples. One straightforward approach is to remove those rows entirely because you can’t train a supervised model without the label (unless the missing target is part of a semi-supervised or unsupervised sub-problem). However, when the proportion of missing targets is large or the data collection process suggests non-randomness, you face potential bias. In such scenarios, consider the following tactics:

• Investigate why these targets are missing. If there is a systematic reason (e.g., certain demographic groups not reporting information), your model might end up biased. • Use additional domain knowledge or proxy measures to approximate the missing target values, but keep in mind that this introduces some noise into the target itself. • Explore semi-supervised techniques if partial supervision can be gleaned from related data or external sources. • Evaluate multiple scenarios (e.g., remove missing target rows vs. attempt to estimate target values) and measure how each approach impacts model performance.

A critical edge case is where missingness in the target variable might correlate with the magnitude of the target (Missing Not at Random). For example, patients with exceptionally high medical bills might be less likely to self-report them. If you remove these cases, you systematically remove large values from your training, creating skewed or incomplete models.

Can we combine multiple imputation methods, and what are the challenges?

Yes, you can combine multiple imputation approaches to tackle heterogeneous data or varying patterns of missingness. For instance, you might use separate specialized methods for different features (e.g., kNN for continuous variables, mode imputation for certain categorical features, and a predictive model for others). Combining these strategies can, however, introduce complexity:

• Coordination: If you separately impute multiple features using different methods, you need a consistent procedure to ensure the imputed values do not contradict each other. Iterative methods (like MICE) attempt to maintain consistency by repeating the imputation cycle until convergence. • Computational Overhead: Each imputation approach adds overhead, especially if you do it repeatedly for multiple features or multiple datasets (as in multiple imputation). • Risk of Overfitting: Advanced or highly tuned imputation on your training set might inadvertently overfit, particularly if you use complex models to impute. This can lead to overly optimistic results during validation but poor generalization on unseen data.

A subtle pitfall here is if one tries to optimize the choice of imputation method based on model performance in a single pipeline. You might inadvertently choose an imputation method that artificially inflates training or validation performance but doesn’t generalize well.

How do we detect and diagnose patterns of missingness before deciding on an imputation approach?

Detecting patterns of missingness involves both statistical and domain-driven diagnostics:

• Data Exploration: Check simple metrics—like percentage of missing values per column—and relationships in the data. For instance, if feature1 is missing only when feature2 is above a certain threshold, that suggests a non-random pattern. • Visual Exploration: Heatmap-based plots (e.g., a matrix showing missing vs. non-missing data) can reveal block patterns or correlated missingness among features. • Statistical Tests: Apply formal tests (e.g., Little’s MCAR test) to see if the data can be assumed MCAR. • Domain Knowledge: Investigate operational or real-world factors behind data collection. Missingness might stem from sensor failures, incomplete questionnaires, or external constraints.

A tricky case arises when missingness occurs in slices of data that reflect real operational differences (e.g., data from sensor_3 is systematically missing every other week). Such time-based or system-based patterns can break MCAR assumptions and render naive imputation invalid.

What specific challenges arise with missing data in time series regression models?

Time series data often contains temporal dependencies that affect imputation strategies:

• Temporal Correlation: If a value is missing at time t, you might need to consider values near t (e.g., t-1, t+1) for effective imputation. A simple mean or global method might ignore local patterns. • Non-Stationarity: Patterns change over time; an approach that works in one time segment may not be valid for another. For instance, a sensor’s baseline drift means older observations might be systematically different. • Seasonal or Cyclical Effects: Missing values in one season might be better informed by other samples within the same seasonal period rather than just adjacent timestamps. • Real-Time Imputation: If the regression model is used in an online or streaming context, you can’t rely on future data. This restricts you to look-back windows rather than full bidirectional context.

An edge case is abrupt shifts or anomalies: if the data experiences regime changes (e.g., a control system changes set points), imputation relying on the older regime might be misleading. Domain-specific strategies—like time series forecasting models (ARIMA, LSTM) purely for imputation—can be more appropriate if the data is strongly time-dependent.

How should we interpret regression coefficients after we have imputed missing data?

Imputation can affect how we interpret the parameters in regression:

• Coefficients Might Shift: By filling in missing values, you possibly alter the overall distribution of each variable. Depending on the imputation method, certain relationships can be strengthened or weakened. • Standard Errors Become Trickier: Standard linear regression assumptions about variance might not hold if the imputed data introduces extra uncertainty. Multiple imputation approaches attempt to quantify this uncertainty, often leading to broader confidence intervals. • Potential Bias: If your imputation was naive (e.g., mean imputation in a dataset that’s not MCAR), the regression coefficients might be biased, especially for variables with high missingness. • Diagnostic Checks: After fitting a regression with imputed data, examine residual plots and measure out-of-sample performance. If the distribution of residuals is skewed or the model systematically under/overpredicts certain segments of the data, it might indicate that the imputation introduced bias.

An example pitfall is concluding that a coefficient is not statistically significant after a naive imputation method, while in reality the missing data mechanism masked the variable’s actual effect.

How to handle missing data in categorical features differently compared to continuous features?

Categorical features require specialized handling:

• Inserting a Special Category: Sometimes you add a category “Missing” to indicate that the value was not observed. This can be effective if “missingness” is itself informative. • Mode Imputation: A simple approach is to replace missing categories with the most frequent category. However, this can inflate that category’s representation, causing potential bias. • One-Hot Encoding Nuances: If you apply one-hot encoding, you must ensure consistent encoding of the “Missing” category across training and test sets. Inconsistency can break the model at prediction time. • Domain Knowledge: Certain categorical variables might be missing for a reason that relates to other features. For instance, if a user never filled out a particular field (like marital status), it might be correlated with certain demographic traits.

An edge case is when a large fraction of the category is missing, making the “Missing” category dominant in the training set. This might overshadow other valid categories, leading to unusual learned relationships and inflated importance for missingness.

How does missing data affect feature selection or regularization in regression?

If you use automated feature selection (like L1 regularization / Lasso) or embedded methods (tree-based feature importance), missing data can distort outcomes:

• Biased Feature Importance: If the imputation consistently assigns certain values (e.g., mean or mode) in a large subset of rows, the variance of that feature could be artificially lowered, influencing how the model ranks it. • Over-Penalization: In regularized models, features with many missing values might get penalized more heavily if the imputation poorly maintains true variance, pushing them toward zero in Lasso. • Interactions with Other Features: If you remove or impute one feature prior to deciding on others, you might inadvertently affect correlated features. Iterative or simultaneous feature selection and imputation strategies can mitigate this but are more complex.

A subtle scenario arises when a feature is heavily missing for a particular sub-population, so its meaning or predictive power might differ between subgroups. If you do not explicitly model these subgroups, you might discard a genuinely predictive feature too early.

Can we combine domain knowledge and external data sources to improve missing data imputation?

In real-world applications, domain expertise or external data can be invaluable:

• Auxiliary Data: Sometimes external datasets or public records can fill in missing values. For example, using census data for missing demographic information. • Logical Constraints: Domain knowledge might inform that certain values can’t exceed a threshold. For instance, a sensor measuring temperature might never exceed 300C under normal operation. This knowledge can guide the distribution from which you draw imputed values. • Causal Knowledge: If you know causal relationships, you can direct your imputation approach. For example, if feature A directly causes feature B, you might prefer a model that uses A to impute B rather than vice versa.

However, a pitfall can be merging external data that is not aligned or matched properly (e.g., different units, different geographical or temporal resolution). Misalignment can lead to misleading imputations if you are not careful about data integration steps.

How do we perform missing data imputation in a streaming environment?

When data arrives in real time:

• Real-Time Constraints: The model might need to make immediate predictions without the luxury of future data. Simple methods (e.g., mean or rolling-window average) are often used initially. • Adaptive Imputation: You can maintain running statistics (like an exponentially weighted moving average) to update imputation parameters on the fly. If the feature’s mean shifts over time, your imputation must adapt. • Online Learning Methods: Some iterative algorithms can update parameters incrementally. For missing data, you might store partial distributions or neighbor indices for kNN-based streaming imputation, though this can be memory-intensive. • Drift Detection: If you detect that data distributions have shifted significantly, you may need to reset or reinitialize your imputation logic.

An edge case is abrupt sensor failures that cause large consecutive blocks of missing data. In such situations, short-window averaging might not be enough, and fallback mechanisms (e.g., alerting system operators) could be necessary if the missingness rate becomes too high to handle reliably.

How do we measure the effectiveness of different imputation strategies?

Measuring imputation effectiveness requires careful design:

• Holdout Subset with Artificial Missingness: One popular approach is to take a subset of the complete data, artificially mask some values, impute them, and compare the imputed values to the actual ones. This measures the reconstruction error. • Downstream Task Performance: Ultimately, we judge imputation by how well the final model performs on a validation or test set. If the predictions improve after using a more sophisticated imputation method, it indicates that your approach to missing data is beneficial. • Distribution Checks: Compare the distribution (mean, variance, skew) of imputed features to that of the original data or known reference distributions. Dramatic mismatches can signal a flawed method. • Confidence Interval or Variance Analysis: For multiple imputation methods, check the variability across different imputations. If the variance is extremely high, it indicates that the method is highly uncertain.

A subtle pitfall is that an imputation strategy might yield lower reconstruction error but not necessarily better downstream regression performance (or vice versa). Balancing these metrics requires careful evaluation to confirm that the chosen method aligns with your end goals.