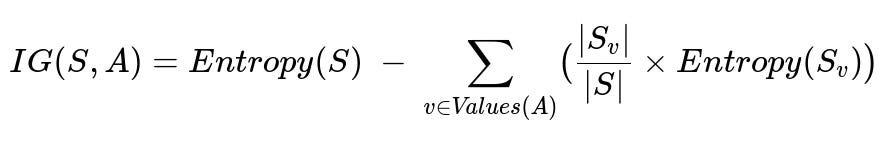ML Interview Q Series: How do you differentiate and evaluate the various methods for generating Decision Trees?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Decision trees can be built using a range of algorithms that select the best feature splits under specific criteria. The most popular methods include ID3, C4.5, and CART. Each algorithm uses a different splitting criterion and has its own strategy for dealing with factors such as continuous attributes, missing values, and pruning. Understanding these algorithms involves exploring how they measure “quality” in each split, the types of data they support, and how they handle overfitting through pruning. Below are several key points related to comparing these algorithms.
Key Differences in Splitting Criteria
ID3 typically employs entropy (as a measure of impurity) and information gain to select the best feature split. C4.5 is considered an extension of ID3, refining aspects like handling continuous values and pruning strategies. CART usually relies on Gini impurity for classification tasks. Although both entropy and Gini measure impurity, they differ in how they weight misclassifications and split preferences.
A core concept for splitting that arises in ID3 and C4.5 is “information gain.” This concept quantifies how well a chosen attribute splits a dataset into classes. The formula for information gain (IG) using entropy is shown below in big font:
Where:
S is the original set of samples before splitting.
A is the attribute (feature) we are splitting on.
Values(A) is the set of all possible values of attribute A.
S_v is the subset of samples where attribute A has value v.
|S_v| is the number of samples in subset S_v, and |S| is the total number of samples in S.
Entropy is computed based on the class distribution in a given set.
Both ID3 and C4.5 focus on maximizing IG in their splits, although C4.5 uses a gain-ratio measure (which normalizes by the intrinsic information of the split) to compensate for biases toward features with many distinct values. CART, by contrast, typically uses Gini impurity, which is computed based on the sum of squared probabilities of each class in the split. Despite these differences, the overall goal is the same: find splits that yield purer child nodes.
Handling Continuous and Categorical Features
ID3 initially was designed for discrete attributes. C4.5 extends this by handling continuous attributes through a thresholding mechanism—essentially trying multiple possible split points based on the data. CART also handles numerical features naturally by splitting on a threshold. The ability to handle continuous data efficiently is an important distinction, since real-world datasets commonly contain numeric features.
Missing Values and Pruning Strategies
Missing data can pose challenges for any decision tree builder. C4.5 uses a technique where it assigns fractional instances to branches, effectively distributing records with missing attribute values across all possible branches (weighted by their likelihood). CART can use surrogate splits—basically using another attribute that best mimics the original split—to handle samples where a feature is missing.
Pruning is essential to prevent overfitting. ID3 did not originally have a sophisticated pruning strategy, whereas C4.5 introduced error-based pruning. CART employs cost-complexity pruning, which involves a trade-off between tree depth and fit. These distinctions in pruning can strongly affect a tree’s interpretability, size, and generalization performance.
Evaluating Model Complexity and Interpretability
Though decision trees are typically considered interpretable, trees that grow large with many levels can lose interpretability in practice. The chosen splitting criterion (entropy, Gini, etc.) can impact how rapidly a tree grows and how many splits are performed. Algorithms that do not regularize or prune aggressively can produce very deep trees. A deeper tree might achieve higher accuracy on training data but risk overfitting.
Practical Implementation Example in Python
Below is a short Python snippet to illustrate how you might compare different splitting criteria using sklearn. While scikit-learn’s DecisionTreeClassifier primarily supports Gini and entropy, you can easily switch between these criteria to see how it affects performance.
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score
# Load example dataset
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Using Gini
clf_gini = DecisionTreeClassifier(criterion='gini', random_state=42)
clf_gini.fit(X_train, y_train)
pred_gini = clf_gini.predict(X_test)
acc_gini = accuracy_score(y_test, pred_gini)
# Using Entropy
clf_entropy = DecisionTreeClassifier(criterion='entropy', random_state=42)
clf_entropy.fit(X_train, y_train)
pred_entropy = clf_entropy.predict(X_test)
acc_entropy = accuracy_score(y_test, pred_entropy)
print("Accuracy with Gini:", acc_gini)
print("Accuracy with Entropy:", acc_entropy)
This code quickly demonstrates how altering the splitting criterion might affect results. Similarly, if you wanted to explore pruning strategies, you could adjust the max_depth or min_samples_leaf.
How Each Algorithm Compares in Practice
ID3 is straightforward but lacks certain extensions that more modern algorithms require (e.g., handling continuous data naturally and pruning). C4.5 improves on ID3 with better handling of numeric data, missing values, and pruning. CART is quite popular and is the foundation of many tree-based ensemble methods (e.g., Random Forests). CART’s computational simplicity and robust pruning methods make it a standard baseline in many tasks.
Common Follow-up Questions
How does overfitting come into play when comparing different Decision Tree algorithms?
Decision trees can easily fit noise in the data if allowed to grow without restraint. ID3, especially in its original form, has no built-in pruning, which makes it prone to creating very deep trees. C4.5 and CART, on the other hand, include systematic pruning procedures to trim back the tree and remove splits that do not significantly reduce error on unseen data. When comparing algorithms, you need to consider how well each prevents overfitting. A powerful splitting criterion is not enough if the tree is not regulated by a robust pruning or stopping method.
Why might we prefer Gini impurity over entropy in some scenarios?
Although entropy and Gini impurity are quite similar in how they measure impurity, Gini impurity can be computationally simpler in certain implementations. In practice, some researchers find that Gini-based splits are a bit faster to compute, and they can lead to very similar decisions compared to entropy-based splits. Moreover, Gini sometimes has a slight bias toward larger or more frequent classes, which can be an advantage depending on the class distribution.
How do we handle missing data or outliers when using these algorithms?
Different implementations have varying ways of dealing with missing values. C4.5, for example, distributes instances among branches proportionally by the likelihood of each branch matching the data point’s other known features, while CART might rely on surrogate splits. As for outliers, decision trees can sometimes be robust because each split is a local decision. However, extreme outliers in continuous features might influence the choice of splits, especially if the algorithm does not incorporate robust data preprocessing or a suitable pruning strategy.
Why might pruning strategies differ among these algorithms?
Each algorithm implements a pruning strategy that reflects its splitting criterion and objective function. ID3 originally did not incorporate a formal pruning approach, whereas C4.5 introduced error-based pruning, which essentially checks whether certain splits produce significantly better accuracy on validation data. CART uses cost-complexity pruning that balances model complexity against its fit. These differences often reflect the historical development of each algorithm and the assumptions regarding data noise and model generalization.
How do we pick the best algorithm for a particular dataset?
Selecting the optimal algorithm involves:
Data properties: If your data has many continuous features or missing entries, C4.5 or CART might be preferable because they handle these scenarios gracefully.
Computational considerations: CART can be computationally efficient and is widely used in large-scale tasks, especially as a base learner in ensemble methods. If you need a lightweight approach, sometimes older algorithms like ID3 or simpler strategies can be sufficient for smaller datasets.
Practical performance and interpretability: You might run each approach on a validation set or use cross-validation to see which yields the best generalization. In practice, especially in large industrial settings, CART-based implementations are common, but the decision ultimately depends on metrics such as accuracy, precision, recall, or any other domain-specific requirement.
By comparing algorithms on the above dimensions—splitting criterion, handling of continuous/missing data, pruning methods, computational efficiency, and interpretability—you gain a comprehensive view of which decision tree approach will best suit your application.