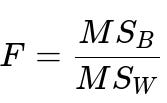ML Interview Q Series: How does an ANOVA test work?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Analysis of Variance (ANOVA) is a statistical method used to determine if there is a significant difference between the means of three or more groups. It does so by examining the variation within each group compared to the variation between groups.

Core Idea

ANOVA partitions the total variability found in the data into two components:

• Variability between the groups (often referred to as "between-group variability").

• Variability within the groups (often referred to as "within-group variability" or "residual variability").

If the between-group variability is sufficiently large relative to the within-group variability, it suggests that at least one group mean is significantly different from the others.

Mathematical Foundation

The key statistic used is often called the F-statistic, which compares the ratio of the mean square between groups to the mean square within groups.

Where:

• MS_B is the "mean squares between groups." It is computed by taking the sum of squares between groups (SS_B) and dividing by its corresponding degrees of freedom (df_B). SS_B is based on differences between each group mean and the overall mean, multiplied by the size of each group.

• MS_W is the "mean squares within groups." It is computed by taking the sum of squares within groups (SS_W) and dividing by its corresponding degrees of freedom (df_W). SS_W represents the variation due to differences within each group.

The degrees of freedom for between-groups variation are typically number_of_groups - 1, and for within-groups variation they are number_of_samples - number_of_groups. The F-statistic follows an F-distribution under the null hypothesis that all group means are equal. We compare the computed F-value to a critical value (or we use a p-value) to decide whether to reject the null hypothesis.

ANOVA Assumptions

ANOVA relies on certain assumptions to ensure validity:

• Normality: The residuals (within each group) are assumed to be normally distributed.

• Homogeneity of variances: Also known as homoscedasticity, each group is assumed to have the same variance.

• Independence: Observations are independently sampled.

When these assumptions are violated, alternative methods (or adjusted ANOVA approaches) may be required.

Practical Steps

To conduct a one-way ANOVA:

• Formulate the null hypothesis that all group means are equal.

• Calculate the group means and the overall mean.

• Compute the sum of squares between groups (SS_B) and within groups (SS_W).

• Divide each sum of squares by its corresponding degrees of freedom to obtain MS_B and MS_W.

• Compute the F-statistic = MS_B / MS_W.

• Determine the p-value from the F-distribution. If the p-value is below your significance threshold (e.g., 0.05), you reject the null hypothesis.

Implementation Example in Python

Below is a small example using Python's scipy.stats library for a one-way ANOVA test. Suppose we have three groups (group1, group2, group3), each representing some observed data:

import numpy as np
from scipy import stats

# Example data for three groups
group1 = [12.2, 13.1, 14.5, 11.9, 12.8]
group2 = [10.1, 9.8, 10.5, 11.0, 10.7]
group3 = [13.5, 14.2, 13.7, 13.9, 14.1]

f_statistic, p_value = stats.f_oneway(group1, group2, group3)

print("F-statistic:", f_statistic)
print("p-value:", p_value)

If the p-value is small (below the chosen significance level), then we conclude there is evidence that at least one group mean is different. To identify which specific groups differ, a post-hoc test (e.g., Tukey's test) is typically performed after a significant ANOVA.

What Happens If the ANOVA is Significant?

When the F-test indicates significance, it only tells you that at least one group mean differs from the others. It does not tell you specifically which pair(s) of groups differ. Hence, if the result is significant, you usually follow up with post-hoc comparisons (like Tukey’s HSD, Bonferroni correction, or others) to identify the group differences while controlling for Type I error.

Follow-up Questions

Could you explain the implications of violating ANOVA assumptions?

Violating assumptions can invalidate the p-value associated with the F-statistic. If normality is violated, you might opt for a non-parametric alternative like the Kruskal-Wallis test. If there is unequal variance across groups (heteroscedasticity), you can use a Welch ANOVA which adjusts for variance differences. Independence is critical, because correlated observations reduce effective sample size and inflate Type I error rate.

It is also possible to perform a data transformation (e.g., log transform) if the data are positively skewed or if group variances increase with the mean.

How do you interpret a significant ANOVA result in real-world scenarios?

Interpretation depends on the context. A significant ANOVA implies that there is a statistically significant difference in average outcomes across groups. In a practical context, you should:

• Confirm that the effect size (e.g., partial eta-squared) is large enough to be meaningful.

• Follow up with post-hoc tests to see where the differences lie.

• Check if your data meets assumptions or consider robust or non-parametric methods if needed.

What is the difference between a one-way ANOVA and a two-way ANOVA?

A one-way ANOVA tests the effect of a single factor with multiple levels on a response variable. A two-way ANOVA extends the idea to include two factors (e.g., factor A with multiple levels and factor B with multiple levels), allowing you to test:

• The effect of factor A.

• The effect of factor B.

• The interaction effect of A and B together.

In real applications, a two-way ANOVA helps you see if the effect of one factor depends on the level of another factor, giving deeper insight into complex experimental designs.

When would you use repeated measures ANOVA?

Repeated measures ANOVA is used when the same subjects are measured under multiple conditions or time points. In this scenario, independence is partially violated because the same entity is repeatedly measured. Repeated measures ANOVA handles this by modeling the within-subject correlation. Common use cases include clinical studies where you measure the same patients’ response before and after treatment, or multiple times over the duration of the study.

How do you control for Type I error in post-hoc comparisons?

When making multiple pairwise comparisons after a significant ANOVA, each additional test increases the probability of a Type I error (false positive). To address this, you often adjust p-values or alpha levels. Common methods include:

• Bonferroni correction, which divides the significance threshold by the number of comparisons.

• Tukey’s HSD (Honestly Significant Difference), which is designed specifically for multiple comparisons in ANOVA.

• Holm or Sidak methods, which are other ways to adjust p-values.

The main idea is to reduce the chance of labeling too many differences as “significant” when performing multiple tests.

How do you handle outliers or non-normal data in ANOVA?

Outliers can have a large impact on the F-statistic. Possible approaches:

• Investigate and clean data: Ensure that outliers are genuine or correct data entry errors.

• Transformation: Apply transformations such as a log transform if outliers distort the variance.

• Robust ANOVA: Use robust versions of ANOVA (like Welch’s ANOVA or a rank-based method).

• Non-parametric test: Use Kruskal-Wallis if the data deviate substantially from normality and if you cannot reasonably transform them into approximate normal distributions.

In practice, it is crucial to understand why outliers exist and whether they reflect a meaningful part of the underlying distribution or data quality issues.

Summary of Key Points

• ANOVA compares multiple group means by splitting total variance into between-group and within-group components.

• It relies on assumptions of normality, homogeneity of variance, and independence of observations.

• The F-statistic helps determine if observed differences in group means are statistically significant.

• Significant ANOVA results indicate that at least one group differs, warranting post-hoc tests to pinpoint specific differences.

• Repeated measures and multi-factor designs (two-way ANOVA, etc.) extend the basic idea to accommodate correlated data or additional factors.

Below are additional follow-up questions

How do you handle missing data in an ANOVA, and what are some potential biases if missingness is not random?

Handling missing data requires careful consideration, as it can alter the representativeness of each group and potentially bias the results. There are several approaches:

• Listwise Deletion: Excluding any cases (rows) with missing values is the simplest approach, but it can drastically reduce your sample size and may distort group balance if data are not missing completely at random (MCAR).

• Mean/Median Imputation: Filling in missing values with a group’s mean or median. This retains sample size but artificially reduces within-group variability and can bias estimates of variance.

• Multiple Imputation: More sophisticated approach where each missing value is replaced with a set of plausible values based on other variables in the dataset. You then run the ANOVA multiple times and pool results. This better reflects uncertainty introduced by missingness.

• Maximum Likelihood Methods: Algorithms (e.g., Expectation-Maximization) that estimate parameters (e.g., group means and variances) by leveraging all available data and modeling the missing mechanism.

If missingness is not random (for example, if values are systematically missing for larger measurements), there can be significant bias. In this scenario, even multiple imputation or maximum likelihood can fail if the model does not correctly account for the reason data are missing. Consequently, sensitivity analyses—testing how different assumptions about missingness affect your conclusions—are crucial.

What is the difference between Type I, Type II, and Type III sums of squares in ANOVA, and why might you choose one over the other?

In designs with more than one factor (e.g., two-way ANOVA) or unbalanced data, different sums of squares (SS) calculations can lead to different results:

• Type I (Sequential) Sums of Squares: Factors are entered into the model in a specified order. The variance accounted for by each factor is measured sequentially. Results can depend on the order of factor inclusion, making Type I SS sensitive to the sequence used.

• Type II (Hierarchical) Sums of Squares: Each factor is evaluated after accounting for all other factors at the same order, excluding interactions. This approach does not test the interaction term and can be misleading if there is a significant interaction.

• Type III (Partial) Sums of Squares: Each factor is evaluated after accounting for all other factors and interactions, regardless of order. This is often favored in unbalanced designs because it tests each main effect and interaction at the same conceptual “level.”

Choice often depends on the research questions and data balance:

• Balanced Data: Type I, II, and III SS will coincide, so there is no discrepancy.

• Unbalanced Data: Researchers frequently use Type III SS because it tests each effect while accounting for all other terms in the model. However, interpretations can be complex if factors are highly correlated or if the model is missing certain terms.

How can you interpret effect sizes in ANOVA, and what do measures like partial eta-squared or omega-squared represent?

Effect size measures supplement p-values by indicating how large the differences are:

• Partial Eta-Squared ((\eta_p^2)): Proportion of total variance in the dependent variable that can be attributed to a particular factor, after controlling for other factors in the model. However, (\eta_p^2) can be somewhat inflated if there are multiple factors or if the model is large.

• Omega-Squared ((\omega^2)): Generally viewed as a less biased estimate of the proportion of variance accounted for by an effect. It often yields a smaller value than (\eta_p^2), reflecting a more conservative estimate of the true effect size.

Interpreting these measures requires context:

• Values near 0 indicate negligible differences among group means.

• Values near 1 (which are rare in real-world scenarios) imply the factor explains nearly all variability in the outcome.

• Different fields have rules of thumb (e.g., small, medium, large effect sizes), but it is always wise to interpret effect sizes in light of domain knowledge and practical significance.

How would you handle unbalanced group sizes in ANOVA, especially if there's a big difference in sample sizes across groups?

Unbalanced group sizes do not invalidate ANOVA, but they can:

• Reduce overall power, particularly for groups with very small sample size.

• Increase the risk that violations of homogeneity of variance (heteroscedasticity) have a larger impact on the test.

• Affect how sums of squares are computed in multi-factor designs (leading to preference for Type III sums of squares).

Potential strategies:

1. Use a Robust ANOVA Approach: Tools like Welch’s ANOVA handle unequal variances and can be more reliable when group sizes differ substantially.

2. Check Assumptions: Ensure group variances are not severely different. If they are, consider transformations or a variance-corrected test.

3. Examine Potential Bias: If group sizes are unbalanced due to a systematic cause (e.g., dropout rates differ among treatment conditions), missingness may not be random.

4. Interpret with Caution: Large differences in sample size mean that certain group estimates might be less precise. Post-hoc power analyses and effect size measures can help contextualize findings.

What are the advantages and disadvantages of using a repeated measures ANOVA vs. a mixed-effects model when you have repeated measurements?

• Repeated Measures ANOVA:

  • Advantages: Straightforward extension of classical ANOVA, widely taught, powerful for detecting within-subject effects.

  • Disadvantages: Assumes sphericity (equal variances of the differences between all repeated measures). Violations of sphericity can cause bias in F-tests unless corrected (e.g., Greenhouse-Geisser). It can be difficult to handle unbalanced or missing data if participants have different numbers of time points.

• Mixed-Effects (Multilevel) Models:

  • Advantages: More flexible. They allow for random effects (e.g., random intercepts for each subject), can handle unbalanced data and missing observations more gracefully, and model complex correlation structures across time or repeated conditions.

  • Disadvantages: More complex to set up, interpret, and diagnose convergence issues. Requires specialized software (e.g., lme4 in R, statsmodels in Python).

In practice, many researchers favor mixed-effects models for repeated measures with any complexity, especially if data collection is unbalanced over time or if some subjects are missing entire measurement points.

When might you consider a hierarchical or nested ANOVA design, and what are potential pitfalls in such complex designs?

A hierarchical (nested) ANOVA is relevant when there is a natural nesting structure in the data. For example:

• Students nested within classrooms, or repeated lab measurements nested within each lab instrument.

• Multiple samples taken from each batch in a manufacturing process, with random differences among batches.

Potential pitfalls:

• Misidentifying the Structure: Failing to specify which levels are random or nested can cause incorrect estimates of variance.

• Over- or Under-Parameterization: If too many random effects are modeled (relative to sample size), the model may become unstable or overfit. Conversely, ignoring nesting can inflate Type I error by treating correlated observations as independent.

• Interpretation Challenges: Partitioning variance across multiple levels can be less intuitive. Researchers must be careful about which effects are fixed (factor of scientific interest) and which are random (nuisance variability).

In practice, how do you decide whether to use parametric ANOVA or a non-parametric test like Kruskal-Wallis, and what are the trade-offs?

• Parametric ANOVA assumes normality (of residuals) and homogeneity of variance. It is more powerful when these assumptions are approximately met. It also provides direct interpretability in terms of means.

• Kruskal-Wallis is a rank-based test that does not assume normality or homogeneity of variance to the same extent. It can be more robust to outliers and skewed data, but it tests differences in median ranks, not group means.

Trade-offs:

1. Power: ANOVA usually has higher power if data are truly normal and variances are equal. Non-parametric methods may lose power in small samples or if there are many ties.

2. Interpretation: ANOVA directly compares means. Kruskal-Wallis detects a difference in distributions; if the shape of distributions differ across groups, interpretation is more nuanced.

3. Sample Size: Non-parametric tests can be appealing if sample sizes are small or if distribution assumptions cannot be validated.

4. Extension: ANOVA can be extended to more complex designs (two-way, repeated measures) more easily. Kruskal-Wallis is limited to one factor unless other specialized rank-based methods are employed.

Can you apply ANOVA to ordinal data, or is it only valid for interval/ratio data? If so, what considerations are needed?

Classical ANOVA is designed for interval or ratio-scale data where distances between points are meaningful. Using ANOVA on strictly ordinal data is typically discouraged because the exact numeric spacing between ranks is not defined. However, some practitioners still apply it to Likert or other ordinal scales under these conditions:

• Large Enough Scale: If the ordinal scale has many categories (e.g., a 10-point scale) and the distribution is approximately continuous, the results may be close to an interval-level interpretation.

• Assumptions: The normality and equal variance assumptions become more delicate because ordinal data might have discrete cutpoints.

• Alternative Methods: Consider non-parametric tests (Kruskal-Wallis for multiple groups) or ordinal regression models specifically designed for ordinal outcomes.

Even if you do apply ANOVA to ordinal data, be transparent about the limitations, and check if the ordinal nature significantly skews the distribution of residuals.

What is the difference between a planned comparison and a post-hoc test in the context of ANOVA, and when should each be used?

• Planned Comparisons (Contrasts): Hypothesis-driven tests decided before seeing the data. Typically used when you have a strong theoretical or practical basis for comparing specific groups (e.g., testing a new drug dose vs. a placebo). Since the number of comparisons is limited and planned a priori, Type I error can be controlled with simpler or no adjustment.

• Post-Hoc Tests: Conducted after discovering a significant overall F-test to see which groups differ. Because multiple pairwise comparisons are often performed, researchers must correct for multiple testing (Tukey, Bonferroni, etc.) to prevent false positives.

The key difference is timing and theoretical basis. Planned contrasts are typically more powerful for specific hypotheses. Post-hoc tests are exploratory and require stricter control of Type I error because no specific group comparisons were identified in advance.

What are the main differences between a frequentist ANOVA and a Bayesian ANOVA approach, and how might results interpretation differ?

• Frequentist ANOVA: Relies on p-values and confidence intervals derived from sampling distributions. You reject or fail to reject the null hypothesis based on a predetermined significance level (e.g., 0.05).

• Bayesian ANOVA: Incorporates prior beliefs and yields a posterior distribution for each parameter of interest. Instead of a single p-value, you get probabilities for hypotheses (e.g., the probability that a certain group mean is higher). This can be more intuitive in expressing how strongly the data support different models or parameter values.

Key differences:

1. Interpretation: Bayesian methods let you say “there is a 95% probability that the mean difference is between X and Y,” whereas frequentist confidence intervals say “if we repeated the experiment many times, 95% of such intervals would contain the true difference.”

2. Prior Information: Bayesian approaches allow incorporation of previous data or expert knowledge, but results can be sensitive to choice of priors if the dataset is small.

3. Model Complexity: Bayesian methods naturally handle complex models, missing data, and hierarchical structures, though at the cost of more computational intensity.

4. Inference: Bayesian analysis provides posterior probabilities of hypotheses or parameter estimates, giving a different perspective than the binary reject/accept framework in frequentist ANOVA.