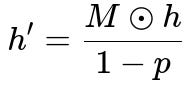ML Interview Q Series: How does randomly dropping certain network connections influence a Deep Learning model’s behavior and performance?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Randomized connection dropping is often implemented as a regularization method called dropout. During training, connections (or neurons) are randomly deactivated according to a given probability, which prevents co-adaptation of features and encourages each neuron to learn more robust representations. This technique helps reduce overfitting, since the network does not rely on specific co-occurrences of neurons to make predictions.

When the network is in the training phase, specific connections are zeroed out with probability p, forcing the model to operate with a smaller effective capacity during each training iteration. During the testing or inference phase, the dropped connections are reactivated, but the learned weights are scaled appropriately so that the expected activations match the training setup. This improves the model’s ability to generalize to unseen data.

Mathematical Formulation of Dropout

Below is a core formula that captures the essence of applying dropout to the output of a particular layer. Let h be the vector of outputs from a layer (before dropout), and let M be the random mask generated from a Bernoulli distribution with parameter (1 - p). Then the dropout operation produces h' as shown in the formula.

Right below are explanations of the terms:

M is a random mask of the same dimension as h. Each element of M is drawn from a Bernoulli distribution with probability (1 - p) for being 1, and p for being 0. In text-based form: M_i is 1 with probability 1 - p, and 0 with probability p. h is the vector of layer outputs (for example, the neuron activations at some layer). p is the dropout rate, representing the fraction of connections (or neurons) that are dropped. h' is the resulting output after the mask is applied. The division by (1 - p) ensures that the expected magnitude of the outputs remains unchanged during training.

Key Considerations for Using Dropout

One consideration involves choosing a suitable dropout rate p. A value too high might cause underfitting because too many neurons or connections are deactivated. A value too low might not sufficiently regularize the network. Typically, p is chosen between 0.2 to 0.5 for many feedforward architectures, but it can vary based on the problem domain and the network architecture.

The scale factor (1 / (1 - p)) is essential so that at inference time, when dropout is turned off, the expected forward pass remains consistent with the training behavior. Without such scaling, the network would see an inflated activation sum at test time because no neurons are dropped.

When using batch normalization in the same network, the ordering of dropout and batch normalization layers can significantly affect training stability and performance. Many architectures place dropout after the activation function but before or after batch normalization depending on empirical performance.

In recurrent neural networks, applying dropout naively inside recurrent connections can sometimes harm the ability of the network to memorize sequences. Techniques such as variational dropout attempt to address this by using the same dropout mask across time steps.

Example in Code

Below is an example of how you might add dropout in a simple PyTorch feedforward network:

import torch
import torch.nn as nn
import torch.nn.functional as F

class SimpleFeedforwardNet(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, p=0.5):
        super(SimpleFeedforwardNet, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.dropout = nn.Dropout(p=p)
        self.fc2 = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.dropout(x)
        x = self.fc2(x)
        return x

# Example usage
model = SimpleFeedforwardNet(input_dim=100, hidden_dim=64, output_dim=10, p=0.5)

In the above snippet, self.dropout(x) will randomly zero out some fraction p of the activations in x. During evaluation (model.eval()), PyTorch automatically disables dropout.

Why Dropout Helps with Generalization

Dropout can be loosely interpreted as training an ensemble of sub-networks. Each mini-batch sees a different connectivity pattern. This randomized training scheme forces the network to rely on more general representations. If certain neurons always co-occurred together during training, the model might overfit. By breaking these co-occurrences, the network learns to distribute its “representational burden” more evenly, resulting in better generalization on test data.

Potential Pitfalls

Overuse of dropout (very high dropout rate) can lead to underfitting. The model might fail to capture enough complexity in the data because too many features are being discarded. Conversely, a tiny dropout rate might not provide sufficient regularization, failing to mitigate overfitting. Balancing these factors often requires cross-validation.

Another subtlety is that some tasks benefit from alternatives to dropout. For instance, in certain convolutional architectures, dropout is replaced or complemented by other forms of regularization like batch normalization or weight decay. Sometimes a small model architecture might not require dropout if the dataset is large enough and well-regularized by other means.

Follow-up Questions

How does dropout differ from other regularization methods such as L2 weight decay?

Dropout works by stochastically deactivating connections/neurons in the network, forcing diverse co-adaptations to break. L2 weight decay shrinks weights continuously to keep them small. While both methods address overfitting, dropout can drastically alter the connectivity pattern each step, whereas L2 weight decay does not change network connectivity; it only constrains the magnitude of weights.

In practice, both dropout and L2 weight decay are often used in combination. L2 weight decay is simpler from a computational standpoint, but dropout typically provides a stronger form of regularization for large, overparameterized neural networks.

When would dropout be insufficient for preventing overfitting?

Dropout can fail when the network is extremely large and the data is insufficiently diverse or complex. If the network’s capacity is huge relative to the dataset, even random connection dropping might not stop the model from memorizing. Another scenario involves tasks that require preserving fine-grained features that get lost when crucial neurons are dropped. In such cases, other techniques such as data augmentation, carefully chosen architectures, or more advanced regularization approaches might be necessary.

Does dropout always improve performance in any layer of a network?

Dropout is often most useful in fully connected layers. In convolutional layers, it can sometimes disrupt spatial feature continuity. That said, many CNN architectures do benefit from dropout in later fully connected layers. When dropout is placed in the earliest layers of the network, the raw representation might become too noisy to be helpful. Deciding where to apply dropout is empirical; typically, deep learning practitioners rely on experimentation guided by knowledge of each layer’s function in the architecture.

What practical guidelines exist for tuning dropout rate?

Fine-tuning dropout rate p requires monitoring validation accuracy and loss. Start with a typical range (0.2 to 0.5) and observe whether the network overfits or underfits. If overfitting is still prominent, increase p in small increments. If the network is underfitting (low training accuracy or high bias), reduce p. In some tasks, particularly in NLP or certain RNN architectures, smaller dropout values (0.1 to 0.3) might be preferred to avoid losing too much sequential information.

Testing multiple values for p is often easiest via a hyperparameter search or grid search, coupled with early stopping based on a validation metric.

Below are additional follow-up questions

How can dropout be combined with other advanced regularization approaches, such as label smoothing or data augmentation?

Combining dropout with label smoothing and data augmentation can be highly beneficial but also poses coordination challenges. Label smoothing reduces the network’s confidence in its predictions by distributing some probability mass over incorrect labels. Data augmentation enlarges the training set with transformed samples, often preventing overfitting through increased data diversity. Dropout targets co-adaptation of neurons by randomly deactivating them. When these methods are combined, each mechanism attacks overfitting from a different angle. However, a potential pitfall occurs if over-regularization emerges. In some instances, combining strong dropout (a high dropout rate p) with aggressive data augmentation or heavy label smoothing can reduce the network’s effective capacity too much, causing underfitting. Careful tuning of each component in synergy is essential. Practitioners usually measure validation performance closely and adjust individual regularization strengths so that the ensemble effect does not hinder convergence or degrade model expressiveness.

What influence does dropout have on training speed and memory usage?

Dropout slightly increases computational overhead because creating and applying the random mask demands additional operations. In frameworks like PyTorch or TensorFlow, this overhead is typically minor compared to the overall forward-backward pass, but it can still be nontrivial if the network has many layers that each apply dropout. Memory usage generally does not skyrocket merely because of dropout, as the mask only needs to store binary values for the active batch. However, large batch sizes combined with multiple dropout layers may incur extra memory overhead. One subtle challenge is that extensive dropout layers—especially in multi-branch architectures—can fragment GPU memory, potentially slowing down training. In practical terms, most modern hardware handles dropout efficiently. But in certain real-time or resource-constrained environments (like on mobile devices), the added computation of dropout might become a bottleneck, prompting exploration of alternative or lighter forms of regularization.

How does dropout impact model interpretability or explainability methods like feature-attribution techniques?

Interpretability methods (for example, Grad-CAM or saliency-based approaches) rely on gradients or activations to highlight which inputs most heavily influence the output. Dropout can introduce stochasticity in these gradients or activation patterns. If dropout is active during interpretation (in some tools, it might be left on unintentionally), explanations can vary between runs because different neurons are dropped each time. This inconsistency makes the interpretation less stable. On the flip side, if the model is well-regularized by dropout during training, it might have learned more generalizable features, which can sometimes lead to more robust saliency maps. The main pitfall is ensuring consistency in interpretability experiments—most frameworks recommend turning dropout off (i.e., model.eval()) before generating final attributions, unless the interpretability method specifically accounts for dropout stochastics.

How do skip connections in residual or highway networks interact with dropout?

Skip connections allow gradients and activations to bypass layers, helping address vanishing or exploding gradients in deep networks. Applying dropout directly on skip connections can disrupt the intended flow of information, sometimes negating the residual benefit. In many residual architectures, dropout is used after convolutional or fully connected layers but kept minimal or avoided on the actual skip paths. If dropout is incorrectly applied within the main skip path, the network might struggle to converge because essential signals are randomly cut off. Another subtlety is that the dropout probability might need adjustment when skip connections are present: large networks with skip connections might overfit less than their non-residual counterparts, so the same dropout rate used in standard architectures might be more aggressive than needed. Testing both with and without dropout on skip paths is recommended, guided by validation metrics.

Why might dropout degrade performance in certain recurrent networks (like LSTM or GRU models)?

Recurrent networks maintain internal states across time steps. Naively applying dropout at each time step can introduce too much randomness, destabilizing the temporal memory. Standard dropout implementations might drop a different set of neurons at each time step, disrupting the sequential flow of information. To address this, specialized methods such as “variational dropout” or “locked dropout” keep a consistent dropout mask across all time steps for a single sequence, reducing harmful noise in the recurrent connections. Nonetheless, there are cases where applying dropout incorrectly (e.g., on hidden states at every timestep with a high p) can severely impair sequence learning. Hence, the main pitfall is inadvertently hindering the temporal continuity that LSTMs or GRUs rely on to capture long-term dependencies.

Does dropout behave differently in self-attention mechanisms compared to typical feedforward layers?

Self-attention mechanisms (like those in Transformers) contain multiple components, including query-key-value computations, attention scores, and feedforward sublayers. Dropout is often employed in two places: on the attention scores (known as “attention dropout”) and on the intermediate feedforward layers. In attention dropout, random elements of the attention matrix are zeroed to prevent the model from over-relying on particular positions. In feedforward dropout, it is similar to standard MLP dropout. A subtlety is that attention dropout can directly affect how tokens attend to each other, which can either improve generalization or hamper the model’s ability to learn critical long-range relationships if used excessively. Meanwhile, feedforward dropout is more akin to typical fully connected layer dropout. Balancing both forms is crucial, as too much dropout can reduce the model’s expressiveness, while too little may lead to overfitting, especially if the model has many layers and heads.

What happens if dropout is applied to the final output layer before predictions are generated?

Usually, it is uncommon to apply dropout directly to the very last layer’s logits because it can add unnecessary stochasticity to the final predictions. For example, if the final output is a probability distribution over classes, dropping connections right before the softmax can yield inconsistent or unstable predictions during training. Additionally, monitoring metrics like cross-entropy loss or accuracy might fluctuate more widely. However, some Bayesian-inspired approaches keep dropout active even at inference (known as Monte Carlo Dropout) to capture predictive uncertainty. In that setup, multiple forward passes with different dropout masks can approximate a posterior distribution over the model’s weights. While it can be beneficial for uncertainty estimation, it can make single-shot predictions less stable, and repeated runs are required to gather an uncertainty estimate. A pitfall arises if one expects deterministic predictions but forgets to disable dropout in the final layer or if the code inadvertently leaves dropout active, leading to inconsistent results in production.

Can dropout hamper knowledge distillation or model compression strategies?

Knowledge distillation transfers “dark knowledge” from a teacher network to a smaller student network. If the teacher uses dropout heavily, the teacher’s output logits might exhibit extra variance. The student tries to mimic these noisy outputs, which can complicate the distillation process. That said, some research indicates that mild dropout during teacher training can encourage smoother probability distributions, potentially making them more instructive. In model compression techniques (e.g., pruning, quantization), dropout might interact unpredictably. For pruning approaches that remove certain weights permanently, having dropout early in training could reduce reliance on specific connections, which might actually synergize with pruning. However, large dropout rates can lead to suboptimal weight distributions if the compression algorithm depends on stable importance estimates of connections or neurons. A potential pitfall is relying on dropout’s random inactivity to interpret which connections are truly critical, which can be misleading if the dropout pattern is not systematically related to connection importance.