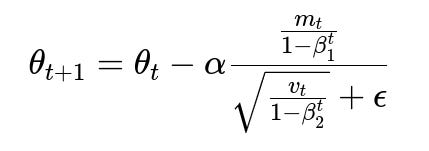ML Interview Q Series: How does the Adam optimizer differ from other optimizers and what specific advantages does it offer?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Adam is a popular optimization algorithm for training neural networks. It combines the benefits of methods like Momentum and RMSProp, allowing for adaptive step sizes for each parameter while also incorporating bias correction terms. The fundamental idea behind Adam is to keep track of two separate moving averages of the gradients during training. One average captures the first moment (akin to momentum), while the other captures the second moment (akin to the uncentered variance of gradients). This helps in adjusting learning rates per parameter dimension more effectively.

Adam is frequently used because it handles noisy and sparse gradients well, and it generally converges faster and more reliably than traditional optimization techniques such as vanilla stochastic gradient descent. The key difference is that Adam updates each model parameter using both the first-moment estimate (which is an exponentially decaying average of past gradients) and the second-moment estimate (which is an exponentially decaying average of past squared gradients). It also applies bias corrections in the early stages of training to account for the initialization of these moving averages.

Below are the most central mathematical expressions that define Adam’s update rules. They show how the first-moment vector m_t and the second-moment vector v_t are updated, and how the final parameter update is performed using these estimates.

Here m_t is the first-moment estimate (momentum-like term), beta1 is the exponential decay rate for the first moment, g_t is the current gradient at time t, and m_{t-1} is the previous first-moment estimate.

Here v_t is the second-moment estimate (similar to RMSProp), beta2 is the exponential decay rate for the second moment, and g_t^2 is the element-wise square of the current gradient at time t.

In this expression, theta_{t+1} is the updated parameter vector, theta_t is the current parameter vector, alpha is the learning rate, and epsilon is a small constant added to the denominator for numerical stability. The terms (1 - beta1^t) and (1 - beta2^t) in the denominator correct for the bias introduced when the running averages are initialized to zero at the beginning of training.

One of the major advantages is that each parameter dimension is updated using an individually adapted learning rate, which can accelerate convergence and reduce the need to fine-tune a global learning rate. It also provides more stable convergence in practice and handles noisy objectives or sparse gradient problems more gracefully than simple momentum-based methods.

Below is a short Python code snippet illustrating a typical use of Adam in PyTorch:

import torch
import torch.nn as nn
import torch.optim as optim

model = nn.Linear(784, 10)  # example linear model for something like MNIST
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# Typical training loop
for epoch in range(num_epochs):
    for images, labels in train_loader:
        optimizer.zero_grad()
        outputs = model(images.view(-1, 784))
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()

The core difference from other optimization algorithms (for example, vanilla SGD with a fixed learning rate) is that Adam computes the step for each parameter based on both the first and second moment estimates of the gradients. Traditional SGD updates parameters based on the current gradient alone, leading to a more uniform learning rate across all parameters. Adam’s adaptive nature means parameters that have had consistently high gradients get lower effective learning rates, while parameters that have had small or infrequent gradients can be scaled up, aiding in faster and more robust convergence.

How Does Adam Differ from Other Methods Like Momentum or RMSProp

Adam can be viewed as a combination of Momentum and RMSProp. Momentum updates maintain an exponential decay average of past gradients, effectively smoothing out oscillations. RMSProp maintains a per-parameter exponential moving average of the squared gradients, adapting the learning rate for each parameter dimension separately. Adam merges these ideas by leveraging both the exponential average of the gradients (momentum aspect) and the exponential average of squared gradients (adaptive learning rates). Moreover, Adam includes bias-correction terms that correct the initial estimates of the first and second moments. This bias correction step mitigates the issue that the estimates m_t and v_t may be biased toward zero when t is small.

Why Adam Is Often Preferred Over Alternatives

It typically converges faster than classical methods in practice, especially on problems with sparse or noisy gradients. It relieves some of the burden of tuning the learning rate, as each parameter’s updates become more refined. Adam is also computationally efficient and has relatively low memory requirements compared to some other adaptive methods. Although there are scenarios where simpler methods like SGD+Momentum might generalize better or be preferred with certain datasets and architectures, the ease of training and the overall good performance make Adam a popular default choice.

Potential Follow-Up Questions

How do you tune the hyperparameters of Adam?

Adam’s default hyperparameters (beta1=0.9, beta2=0.999, epsilon=1e-8) generally work well in many cases. Occasionally, adjusting beta1 or beta2 can help if gradients exhibit highly varying magnitudes or if the training is unstable. The primary hyperparameter that often still needs tuning is the learning rate alpha. In some tasks, smaller or larger alpha may lead to better results.

Are there any disadvantages of using Adam?

Some practitioners observe that Adam might result in models converging to solutions with slightly worse generalization performance compared to SGD with Momentum on certain datasets, especially large-scale image tasks. Adam also has a potential issue called “decoupled weight decay,” which requires careful implementation of weight decay or L2 regularization. PyTorch offers separate parameters for weight_decay to address this issue properly. Furthermore, Adam can become trapped in local minima for certain architectures if hyperparameters are not chosen carefully.

When might you prefer plain SGD with Momentum over Adam?

SGD with Momentum can sometimes yield better generalization and can also scale more predictably with large batch sizes. If one can effectively tune the learning rate and schedule, SGD with Momentum can be very efficient. Tasks with stable and dense gradients, or problems known to benefit from carefully crafted learning rate schedules, may perform better with SGD. Memory usage is also slightly lower with plain SGD because it does not require maintaining additional moment arrays for each parameter.

Can Adam handle sparse gradients?

Adam can handle sparse gradient updates because it adapts the learning rate for each parameter individually. This feature is especially useful in natural language processing tasks with large vocabularies or other situations where gradient updates for many parameters can be zero most of the time. The first and second moment estimates can still be applied adaptively to active parameters without significant penalty to inactive ones.

What is AMSGrad, and how does it differ from Adam?

AMSGrad is a variation of Adam designed to address potential convergence issues. It ensures that the second-moment estimate v_t does not decrease over time by keeping track of the maximum of past v_t values. This modification can improve the theoretical convergence properties of Adam. However, in many practical scenarios, standard Adam performs well enough that AMSGrad might not be necessary.

Below are additional follow-up questions

Could you discuss the role of the epsilon hyperparameter in Adam, and what happens if it’s set too large or too small?

The epsilon parameter is a small constant added to the denominator in the Adam update equation to avoid division by zero. In plain text, the update can be written as: parameter_{t+1} = parameter_t - alpha * (m_t / (1 - beta1^t)) / (sqrt(v_t / (1 - beta2^t)) + epsilon). Without epsilon, if v_t becomes extremely small for any dimension, the optimizer might encounter numerical instability. However, there are edge cases to keep in mind:

• If epsilon is too large, it effectively inflates the denominator, causing each parameter update to be smaller than intended. This could slow down training or lead to the optimizer under-adjusting parameters.

• If epsilon is too small, you might still run into numerical instability, especially on hardware where floating-point computations have limited precision. Extremely small epsilons also risk division by near-zero values, causing large, unstable updates.

In practice, typical values like 1e-8 strike a good balance, but sometimes you see 1e-7 or 1e-6 if training exhibits heavy fluctuations. One should keep an eye on learning curves and gradient norms to detect instability or slow convergence that might point to adjusting epsilon.

How does Adam compare to other adaptive methods like Adagrad or Adadelta, and are there scenarios where those might be preferred?

Adam, Adagrad, and Adadelta all adapt the learning rate on a per-parameter basis, but they manage the accumulation of gradients differently:

• Adagrad accumulates the square of gradients across training steps without decay. This can cause the effective learning rate to shrink rapidly and often requires manual scheduling or resetting of its accumulators if training runs for many steps.

• Adadelta addresses the rapid shrinkage issue by normalizing updates with a decaying average of squared gradients. It removes the need for a base learning rate but can be sensitive to the decay rate hyperparameter.

Adam can be seen as a more general solution that keeps track of both first and second moments with exponential decay. It provides bias correction for both terms and thus can stabilize training early on. However, there are specific domains where Adagrad or Adadelta might still be used:

• Sparse feature spaces: Adagrad can perform well if each feature rarely activates, though Adam also handles sparsity effectively.

• Situations requiring no explicit learning rate: Adadelta removes the need for a global alpha, which might be convenient if tuning alpha is challenging.

A potential pitfall arises if a practitioner mechanically defaults to Adam without checking whether a simpler method (like Adagrad) might handle the problem’s sparsity or one-hot representation more effectively. Always evaluate test metrics and watch for training instabilities before finalizing your choice.

Under what circumstances could Adam experience gradient explosion or vanishing, and how might you mitigate these issues?

Adam can, in rare cases, still face exploding or vanishing gradients:

• Exploding gradients: This might occur if your model architecture is deeply recurrent or if your loss suddenly spikes due to outlier data or a drastic shift in the input distribution. Since Adam adapts learning rates per parameter but does not directly clip gradients, large gradient norms can still lead to abrupt parameter changes. Mitigation strategies include gradient clipping (common in recurrent neural networks) or carefully monitoring the learning rate and moment parameters.

• Vanishing gradients: If the second moment (v_t) grows disproportionately large for certain parameters, it can significantly reduce update magnitudes. Very deep network architectures without proper initialization or skip connections may still suffer from vanishing gradients. Strategies like using residual connections, batch normalization, or carefully tuning the network design can help. Although Adam’s adaptive nature reduces the risk of extreme vanishing, it doesn’t completely eliminate it.

One subtle pitfall is that if the second moment estimate grows for almost all parameters (for example, in certain types of noisy tasks), training may slow drastically. Monitoring gradient norms and the magnitude of updates can detect these issues early.

How well does Adam scale to extremely large models, and what kind of memory constraints should we watch out for?

For each parameter, Adam stores and updates two additional buffers: the first-moment estimate (m_t) and the second-moment estimate (v_t). In large-scale scenarios where models have tens of billions of parameters (e.g., many modern language models), these two extra tensors can significantly increase the overall memory footprint. Potential pitfalls include:

• Exceeding GPU memory or system memory capacity, leading to out-of-memory errors.

• Slower training speed because reading and writing large buffers can become a bottleneck.

To address these concerns:

• Mixed-precision training can lower the memory requirements for storing parameters and gradient buffers.

• Optimizer sharding (in distributed training frameworks) partitions parameters across multiple nodes or GPUs, distributing the storage of these moment estimates.

• Using more memory-efficient variants of Adam (e.g., Adafactor for large language models) can help reduce overhead. However, these methods may require careful tuning to match Adam’s stability.

How does Adam handle gradient noise differently, and can high noise levels affect its updates compared to standard SGD?

Adam adapts its per-parameter learning rate based on recent gradient magnitudes. This can smooth out the influence of random fluctuations, making it less sensitive to noisy gradient estimates. However, in situations where the noise is extremely high or the data distribution is shifting:

• Adam’s v_t might inflate if the mean of squared gradients is large over many steps, which could reduce step sizes more than desired.

• If beta1 is too high, Adam might overly rely on historical gradients, causing updates to be sluggish in adjusting to rapid changes in gradient direction.

With standard SGD, higher noise typically requires adjusting the global learning rate or applying momentum to reduce the variance of updates. In Adam, an alternative approach is to tune beta2 to manage how quickly second-moment estimates adapt to changes in gradient variance. Monitoring the training loss curve over time can help ensure you’re not dampening updates excessively in the face of high noise.

Is there ever a reason to switch from Adam to another optimizer during the same training run?

Yes. Some practitioners use Adam for the early phases of training to achieve quick convergence and then switch to SGD with Momentum for fine-tuning or later stages. This is sometimes done because:

• Adam finds a region of the parameter space that’s reasonably good.

• SGD with Momentum may explore that region with a different update dynamic, possibly settling into minima that generalize better.

However, this approach should be done carefully:

• Sudden switching might introduce instability if the learning rates or momentum terms are not adjusted properly for the new optimizer.

• If the momentum buffers or second-moment estimates are not re-initialized, you may inherit stale or incompatible statistics from the Adam phase.

A smooth transition can be handled by gradually transferring Adam’s learning rate schedule to an equivalent schedule for SGD. Nonetheless, the main pitfall is abruptly changing the optimization landscape without properly accounting for differences in how each optimizer updates parameters.

How does weight decay interact with Adam, and why is it sometimes handled differently compared to L2 regularization?

Weight decay and L2 regularization aim to reduce overfitting by penalizing large weights, but the way they integrate with Adam can differ from naive L2 penalty:

• Weight decay: Often implemented as a direct subtraction of weight_decay * parameter from the parameter update each step. This decouples the regularization term from the gradient of the loss itself, ensuring a consistent shrinkage rate of the parameters.

• L2 regularization: Multiplies the parameter by some factor (1 - alpha * lambda) when computing gradients. With Adam, the per-parameter adaptive scaling can interfere with this approach, sometimes leading to inconsistent or unintended regularization effects.

A subtle pitfall is using L2 regularization by simply adding a weight penalty to the loss in the typical Adam pipeline. This might yield different dynamics than expected because the penalty is scaled by the adaptive learning rate. If you truly want a consistent shrinkage effect, you can use the “decoupled weight decay” version of Adam (for example, torch.optim.AdamW in PyTorch), which handles this separation more elegantly. This is especially important in large-scale models where controlling overfitting is crucial and the interplay of adaptive learning rates and regularization can lead to non-trivial effects.