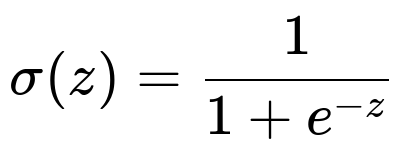ML Interview Q Series: How does the Softmax function differ from the Sigmoid function?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Sigmoid and Softmax are both activation functions frequently utilized in neural networks. They serve different purposes, particularly in classification tasks. Sigmoid is usually employed for binary classification or as an activation for output neurons when modeling a single probability. Softmax is commonly used for multi-class classification, particularly when classes are mutually exclusive.

Sigmoid Function

The sigmoid function takes a real number and squashes it into the range between 0 and 1. It is often used to represent the probability that a particular observation belongs to a certain class in a binary classification setting. Its formula in big h1 font and LaTeX is shown below.

Here z is a real-valued input (the logit). If z is large and positive, e^(-z) becomes very small, and thus the sigmoid approaches 1. If z is largely negative, e^(-z) becomes very large, and the sigmoid approaches 0. For a single output neuron in a binary classification problem, sigmoid is a natural choice to interpret the output as a probability.

Softmax Function

Softmax generalizes the sigmoid function to multiple classes. It takes a vector of real numbers and transforms it into another vector of the same length, where each component lies between 0 and 1, and all components sum to 1. This makes Softmax particularly suitable for multi-class classification tasks with mutually exclusive classes.

Below is the Softmax formula in big h1 font and LaTeX format.

In this formulation, z_i represents the logit for the i-th class, and K is the total number of classes. The numerator e^{z_i} scales the output based on the exponent of the logit value, and the denominator normalizes the sum of all exponentiated logits so that the outputs become a valid probability distribution.

Practical Usage Differences

Softmax is almost always used when there is exactly one correct class among multiple options (i.e., multi-class, single-label classification). The output vector from the Softmax layer is fed into a categorical cross-entropy loss function, guiding the neural network to assign high probability to the correct class and low probability to the others.

Sigmoid is often employed in scenarios where one wants a probability-like output in the range 0 to 1 for each individual label. It is prevalent in binary classification tasks (for example, spam vs. not spam). Sigmoid can also be used for multi-label classification, where each label can be present or absent independently.

Behavior in Multi-Class vs. Multi-Label Tasks

When classes are mutually exclusive, Softmax forces a sum of probabilities equal to 1 across all classes, effectively making one class more probable at the expense of others. On the other hand, when multiple labels can be valid at once, Sigmoid can handle each label independently by producing separate probability outputs.

Gradient Saturation and Training Stability

A known issue with sigmoid is saturation, which can lead to very small gradients. If the input is very large in positive or negative sense, the gradient becomes almost zero, slowing down training. Softmax can also suffer from numerical instability if logits are extremely large in magnitude; however, modern libraries incorporate stability tricks (such as subtracting the maximum logit) to mitigate this problem.

Implementation Example in PyTorch

Below is a brief Python snippet demonstrating how you would apply Softmax and Sigmoid in a simple classification context.

import torch
import torch.nn as nn
import torch.nn.functional as F

class SimpleModel(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(SimpleModel, self).__init__()
        self.linear = nn.Linear(input_dim, output_dim)

    def forward(self, x):
        logits = self.linear(x)
        # For multi-class classification with a single label
        # return F.softmax(logits, dim=1)

        # For binary classification or multi-label classification
        return torch.sigmoid(logits)

# Example usage
model = SimpleModel(10, 3)  # Example with 3 output classes
input_tensor = torch.randn(5, 10)  # Suppose batch of size 5
output_logits = model(input_tensor)

print(output_logits)

In the comment, you can see how to choose Softmax if you are dealing with a multi-class problem where only one of the 3 classes is correct, or Sigmoid if you are dealing with multi-label or binary classification.

How can I decide which one to use?

When you are working with a binary classification or multi-label classification problem, you typically use sigmoid activation on each output neuron and pair that with a binary cross-entropy loss. When you are working with a single-label multi-class classification, you generally use a single Softmax activation (one for all classes) and a categorical cross-entropy loss.

What are common pitfalls and edge cases?

One pitfall occurs if you mistakenly use sigmoid for multi-class, single-label classification. The model might not learn well because there is no competition enforced among classes, and probabilities will not necessarily add up to 1. Conversely, using Softmax for multi-label classification incorrectly forces all probabilities to sum to 1, making it impossible to assign high probabilities to multiple labels simultaneously. In real-world problems, these mistakes can lead to suboptimal or incorrect modeling of the underlying task.

How to handle numerical instability in Softmax?

Softmax can overflow if the logits are very large. Modern deep learning frameworks usually solve this by subtracting the maximum logit from all logits before exponentiation. If you are implementing your own Softmax, you can do:

def stable_softmax(logits):
    max_logit = torch.max(logits, dim=1, keepdim=True)[0]
    exps = torch.exp(logits - max_logit)
    return exps / torch.sum(exps, dim=1, keepdim=True)

This technique helps avoid overflow or underflow by shifting the logits such that the largest logit becomes 0. The shape of the probability distribution remains unchanged.

Could Softmax be used in multi-label tasks?

It is technically possible to use Softmax in multi-label tasks, but it would be conceptually incorrect if you want independent probabilities for each label. Softmax imposes a single-label constraint by normalizing all outputs to sum to 1. Therefore, if you need to output multiple valid classes simultaneously, sigmoid is more suitable, because it does not force probabilities across labels to be mutually exclusive.

What is the gradient of the Softmax function?

If you want to see how the gradient is derived, note that the partial derivative of the Softmax output for the i-th class with respect to the logit for the j-th class involves the output of both i and j. Specifically, it equals Softmax(z_i) * (delta_{ij} - Softmax(z_j)), where delta_{ij} is 1 if i = j, otherwise 0. Although not always computed manually by practitioners, understanding this helps you reason about how changing the logit for one class affects the probabilities for all classes.

How do I choose an appropriate loss function?

For binary outputs (whether single binary classification or multi-label scenarios), binary cross-entropy is typically used. For multi-class single-label classification, categorical cross-entropy is standard. Each of these loss functions is tailored to the range and interpretation of outputs provided by sigmoid and Softmax, respectively.

When to prefer Sigmoid over Softmax in real-world applications?

Use sigmoid when you are dealing with:

• A single neuron output for a binary decision.

• Multiple independent labels that can each be 0 or 1.

Use Softmax when you are dealing with:

• Multiple classes, exactly one of which is correct for each instance.

The decision ultimately comes down to whether or not you want to enforce a mutually exclusive constraint among the different classes or labels.

Could you illustrate both in the context of a real classification example?

Imagine an email classification system:

• If you classify emails into "spam" vs. "not spam," you typically use a sigmoid output, because it is a single binary decision with one output neuron.

• If you classify emails into categories like "social," "promotional," "primary," and you assume only one of these can be correct, you typically use a Softmax layer with three neurons, each representing one category.

If you had an email system that can assign multiple tags like "work-related," "family-related," and "requires-immediate-reply," you would probably use a sigmoid output for each tag independently, because multiple tags can be valid for the same email.

Additional Follow-Up Questions

How do we train a multi-label classifier with Sigmoid outputs?

To train a multi-label classifier, each output neuron is assigned its own probability for a label’s presence or absence. You typically apply a sigmoid activation on each output and use a binary cross-entropy loss term for each label. The final loss is often computed by averaging or summing the individual losses across labels.

What if I want to use a temperature parameter with Softmax?

You can incorporate a temperature T by modifying the logits: z_i / T before computing Softmax. A higher T will produce a more uniform distribution, while a lower T produces a distribution more heavily concentrated around the largest logit. This is sometimes used in knowledge distillation or to control how “confident” the Softmax distribution is.

How do I handle class imbalance in either setting?

For binary classification or multi-label tasks using sigmoid, you can weight the binary cross-entropy loss by class frequencies. For multi-class tasks using Softmax, you can similarly apply weighting factors in the categorical cross-entropy loss. This approach helps mitigate bias toward majority classes and improves performance on underrepresented classes.

Are there any scenarios where a custom activation might be preferable?

In some specialized tasks, researchers might employ custom activations (for example, the log-softmax for numerical stability in certain contexts, or the Gumbel-Softmax trick for sampling discrete categories). Generally, sigmoid and Softmax suffice for most standard classification tasks, but advanced techniques can be introduced for specific research goals or when dealing with discrete latent variables.

Below are additional follow-up questions

How does the choice between Sigmoid and Softmax affect backpropagation and the shape of the error surface?

One of the central considerations in neural network training is how the activation function influences backpropagation. The derivatives of both Sigmoid and Softmax vary, but in different ways that can impact gradient flow.

When you use Sigmoid in a multi-label scenario, you are effectively computing the gradient separately for each output neuron. Each output probability is updated independently, which can simplify certain tasks if labels are independent. However, the derivative of the Sigmoid can become very small once the neuron is saturated in either the 0 region or the 1 region. This leads to slower training in practice if care is not taken (e.g., appropriate initialization, proper learning rates, or batch normalization).

In contrast, Softmax ties the probabilities of all classes together. Changes in one class’s logit affect the probabilities of all the others, creating a coupling that can accelerate the shift in probabilities for mutually exclusive classes. This can be beneficial for tasks where a single correct class must dominate. However, numerical instability can arise if logits are not handled carefully, and a large number of classes can slow down computation, especially in the normalization step for large-scale classification tasks.

A hidden pitfall is the interpretation of local minima or saddle points. In practice, neural networks are known to have a highly non-convex error surface. Sigmoid-based multi-label tasks can easily get stuck if many outputs saturate. Softmax, by normalizing across classes, might push the network away from certain undesirable minima when classes are strongly correlated. Nonetheless, strong class imbalance or very high-dimensional outputs can still lead to suboptimal plateaus or slow gradient flow.

How might domain constraints guide the selection between Sigmoid and Softmax?

Certain real-world domains impose specific requirements on how you represent probabilities. If your domain inherently enforces that only one label can be correct (e.g., an image can only belong to one of several species in a classification problem), Softmax is more suited because it naturally models exclusivity by ensuring probabilities sum to 1.

On the other hand, if the domain allows for overlapping categories (like tagging multiple symptoms in a medical diagnostic system), Sigmoid is more appropriate. Each label’s presence is modeled independently, which aligns with the fact that a single patient can exhibit multiple symptoms simultaneously.

A related pitfall arises when domain knowledge is ignored, and a developer chooses Softmax for a problem that actually requires multi-label classification. This leads to artificially constraining each example to exactly one label, preventing the model from correctly learning independent probabilities for each label. Another subtle issue emerges when domain constraints are uncertain; for instance, if classes are “almost” exclusive but with occasional overlaps, it may be necessary to consider a tailored approach that modifies the standard Sigmoid or Softmax to incorporate partial exclusivity.

Is there a scenario where you might combine Sigmoid and Softmax in the same model?

In certain complex architectures, you might have a multi-class classification branch and a separate multi-label classification branch. For example, if you have a hierarchical classification system where the top layer identifies the broad category (e.g., type of product in an e-commerce setting, using Softmax because the product can belong to one main category), and a second layer identifies multiple applicable sub-features (e.g., product attributes like color, brand, or style, each being independent and modeled with Sigmoid).

This design can appear in multi-task learning setups, where each task has its own output structure. Care needs to be taken with how you combine losses (for example, you might have a categorical cross-entropy loss on the Softmax output and multiple binary cross-entropy losses on the Sigmoid outputs). The main pitfall is ensuring these tasks do not interfere destructively with each other’s training signals, leading to a suboptimal compromise in the shared layers.

What if you have a multi-class problem but classes are not strictly mutually exclusive?

A strictly multi-class problem assumes that only one label is correct for each example. However, some real-world scenarios blur this assumption. For instance, consider music genre classification where a track might predominantly belong to one genre but also have characteristics of others. If the classes are not entirely exclusive, using Softmax forces the probabilities to sum to 1 and overlooks partial membership.

Choosing Sigmoid in this scenario allows each genre to be scored independently. You can threshold or rank outputs to decide whether a class is present or absent. A pitfall is that the data might not clearly define partial membership. You need consistent labels that reflect these overlapping classes. If training data is mislabeled (like incorrectly forcing a single genre on each track), switching to Sigmoid could cause confusion unless the labeling process is corrected.

How can we interpret confidence levels in Sigmoid vs. Softmax outputs?

For Sigmoid, the output of each neuron can be interpreted as an independent probability that a certain label is present. A value close to 1 for a label means high confidence that the label applies; a value near 0 means low confidence. Because they’re independent, summing these probabilities across labels doesn’t necessarily have a meaningful interpretation.

By contrast, a Softmax output near 1 for a specific class i indicates the model’s high confidence that class i is the correct one, and near 0 for other classes implies strong rejection of those. Since probabilities sum to 1, we can interpret the distribution as how the model ranks all possible classes for a given input. A common pitfall is misreading a Softmax probability as an absolute measure of correctness. A class can have a high Softmax value simply because all other classes had even lower logits, not necessarily because the class’s logit is very large in an absolute sense.

How does label smoothing interact with Sigmoid or Softmax-based outputs?

Label smoothing is a technique often used to prevent overconfidence in classification. For Softmax-based classification, you might replace the hard 1 and 0 for the correct and incorrect classes with slightly “softer” targets (e.g., 0.9 for the correct class and 0.1 divided among the remaining classes). This encourages the model to be less overconfident, which can improve generalization. However, label smoothing can introduce subtle biases in reported probability metrics, as the network no longer aims for a strict 1 for the correct class.

For Sigmoid-based multi-label classification, label smoothing can be applied independently to each label. Each label’s target might be turned from 1.0 to something like 0.9. One pitfall here is that, unlike Softmax, your outputs are not being normalized across labels. Thus, the effect of label smoothing on each label is isolated, and you must ensure that the ratio of positive to negative examples still holds or you may skew the probabilities in ways that reduce performance if not tuned carefully.

How do we handle a scenario where we transition from a binary classification to a multi-class classification model?

Sometimes a project may begin with a binary classification approach—for instance, “relevant” vs. “not relevant” content. Later, you might refine the classes to be more specific (“Sports,” “Politics,” “Entertainment,” etc.). In this transition, you might switch from a Sigmoid output (if you only had two classes) to a Softmax output with multiple classes.

A real-world pitfall is not adapting the network architecture or the dataset properly. For example, you might inadvertently keep using a binary cross-entropy loss when you have more than two exclusive categories, leading to inconsistent training signals. You also need to check your data labeling because the assumption has changed from a single binary decision to multiple mutually exclusive categories. If your data is not mutually exclusive, but you force Softmax, you’ll misrepresent how these categories can overlap. Ensure your labeling strategy aligns with the fundamental assumption behind the activation function.

What if we wanted to incorporate prior knowledge about class relationships in a multi-class scenario with Softmax?

In certain tasks, you may have domain knowledge that some classes are more similar or share certain traits. Softmax itself treats classes as distinct outputs without explicit awareness of inter-class relationships beyond competition for probability mass. If you want to encode prior knowledge—say, certain classes are subsets of others, or some classes are more likely to occur if others are present—you may need to adjust your approach.

One method might be to design a hierarchical Softmax where classes are structured in a tree (for example, hierarchical language models). Another approach could be to factorize Softmax into multiple stages, each focusing on subsets of classes. A potential pitfall is incorrectly specifying these relationships, resulting in a misalignment between the model’s structure and the true data distribution. Overfitting or rigid constraints can also occur if the prior knowledge is not entirely accurate, leading to reduced flexibility in the model.

How to interpret the logit values for debugging or model interpretability in the context of Sigmoid vs. Softmax?

Logits are the raw values before Sigmoid or Softmax activation. For a Sigmoid output neuron, a large positive logit (say, 10) implies a probability very close to 1, whereas a large negative logit (say, -10) implies a probability near 0. For Softmax, you have a logit for each class, and the relative differences in these logits drive the final probabilities.

An effective debugging strategy is to look at these raw logits to understand how strongly the model is leaning toward certain classes or labels before the exponential scaling. For example, two classes might both have moderately high logits, but one might be just slightly larger than the other, leading to a strong difference in the final Softmax probability. In practice, you can detect numerical anomalies or initialization issues by consistently seeing extremely large or extremely small logits. One pitfall is forgetting that a high logit for one class might not always mean a proportionally high probability if other logits are also large.

What are the differences in computational cost or memory usage between these activations in large-scale models?

Both Sigmoid and Softmax are fairly cheap operations on modern hardware when dealing with moderate output dimensions. However, in extremely large-scale multi-class problems—e.g., language models that predict thousands or tens of thousands of possible tokens at each step—the Softmax normalization step can become a computational bottleneck, because you must exponentiate and sum across all classes.

Some advanced techniques, such as hierarchical or sampled Softmax, are used to reduce the computational burden in large vocabularies. With Sigmoid in multi-label tasks that have a large number of possible labels, you compute a separate Sigmoid for each output. This can also be expensive if you have a vast label space, but it scales more linearly with the number of labels. A subtle pitfall can occur in memory usage if each label has its own set of parameters and outputs, particularly in large-scale multi-label problems, leading to high memory demands and slower training if not managed efficiently.