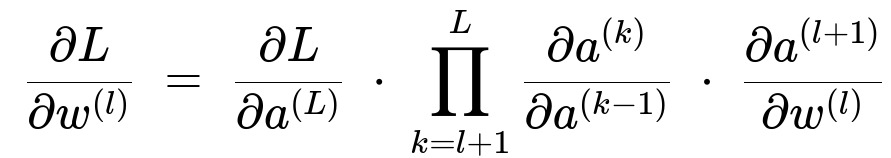ML Interview Q Series: How does the behavior of a neural network change when you reduce its layer width but increase its depth?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Shifting from a neural network that has broader (wider) layers to one that is deeper (with more layers but fewer neurons per layer) can alter the model’s representational power, training dynamics, and generalization properties. Widening a neural network often increases its capacity to memorize data, while making it deeper can enhance the ability to learn progressively more abstract representations. Deeper architectures, however, are prone to issues such as vanishing or exploding gradients, which can make training difficult.

Deeper networks can capture compositional structures more efficiently by stacking multiple nonlinear transformations. Even with fewer units per layer, each additional layer adds new transformations that can yield more complex decision boundaries. For example, certain functions that would require a very large (wide) shallow network might be realized by a smaller number of parameters if arranged in deeper stacks of layers.

Nevertheless, deeper networks can be harder to train. The gradient signal that updates the earlier layers diminishes rapidly as it propagates backward through many layers. This phenomenon is known as the vanishing gradient problem, which can slow or even halt training for deeper architectures if not appropriately addressed with techniques such as careful weight initialization, normalization, and skip connections.

Below is one central expression illustrating the chain rule for backpropagation through multiple layers. This formula emphasizes how the gradient at the final layer is multiplied by partial derivatives in each layer, potentially causing gradients to vanish or explode when many layers are involved.

where L is the loss function, w^(l) is the weight parameter at the l-th layer, a^(l) is the activation at the l-th layer, and the partial derivatives represent the local sensitivities of each layer’s transformation. In very deep networks, the product of many small factors can lead to extremely small (vanishing) or extremely large (exploding) gradients.

In practice, deeper networks often benefit from modern techniques such as skip or residual connections, which help the gradient flow directly from later layers to earlier layers. This eases the training of models that are significantly deeper than what was feasible before. Thus, while going deeper (and narrower) can lead to more powerful abstractions, it can also introduce optimization and generalization challenges that must be addressed through architecture choices, careful initialization, and effective regularization.

A minimal code snippet in PyTorch illustrating the difference between a shallow wide network and a deep narrow network is shown below.

import torch
import torch.nn as nn
import torch.nn.functional as F

# Shallow and wide
class ShallowWideNet(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(ShallowWideNet, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return x

# Deep and narrow
class DeepNarrowNet(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, depth=4):
        super(DeepNarrowNet, self).__init__()
        # Create multiple linear layers each with relatively fewer neurons
        layers = []
        layers.append(nn.Linear(input_dim, hidden_dim))
        for _ in range(depth - 1):
            layers.append(nn.Linear(hidden_dim, hidden_dim))
        self.layers = nn.ModuleList(layers)
        self.final = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):
        for layer in self.layers:
            x = F.relu(layer(x))
        x = self.final(x)
        return x

# Example usage
input_dim = 100
hidden_dim = 1024  # Wide layer
output_dim = 10
depth = 6

wide_model = ShallowWideNet(input_dim, hidden_dim, output_dim)
narrow_model = DeepNarrowNet(input_dim, 64, output_dim, depth=depth)

sample_input = torch.randn(1, input_dim)
wide_output = wide_model(sample_input)
narrow_output = narrow_model(sample_input)

In this example, ShallowWideNet has a single hidden layer with a large number of neurons (i.e., a wide layer), whereas DeepNarrowNet has multiple layers with comparatively fewer neurons each, creating a deeper architecture.

How does depth influence representational power?

Deeper networks allow for hierarchical feature extraction. Each layer can learn increasingly high-level representations, which can reduce the total number of parameters needed to represent certain complex functions. However, if a network is not correctly regularized, it can still overfit or be difficult to train when it becomes too deep.

Why can deeper networks be harder to train?

Training difficulty primarily arises from vanishing or exploding gradients. As seen in the chain rule expression, the gradient’s magnitude can shrink or grow as it propagates through many layers. This makes parameter updates in earlier layers slow or erratic. Techniques like residual connections, careful initialization, batch normalization, and appropriate activation functions can mitigate these problems.

How do skip or residual connections address training difficulties?

Skip (residual) connections add pathways that bypass one or more layers. This means the gradient signal does not have to multiply through as many transformations, making it less prone to shrinking or blowing up. Residual architectures, such as those popularized by ResNet, have shown that extremely deep networks can still be trained effectively.

Are deeper networks always better than wider ones?

A deeper network is not necessarily always better. Sometimes a wider shallow network can achieve similar or better performance, especially if the data is not complex enough to require many layers of abstraction. Depth also increases the risk of overfitting and computational overhead. Ultimately, architecture choice depends on the nature of the problem, the availability of training data, and compute resources.

How can you mitigate vanishing gradients?

Adopting residual connections, carefully selecting activation functions (for example, ReLU, leaky ReLU, or variants that maintain stronger gradients), applying batch normalization, and using proper initialization methods all help alleviate vanishing gradients. These strategies ensure the gradients neither diminish nor explode as they flow through the layers.

What is the role of regularization in deeper networks?

Deeper networks typically have a large number of parameters and can easily overfit. Regularization techniques such as dropout, weight decay, and data augmentation are pivotal in controlling overfitting. Early stopping and careful hyperparameter tuning (especially for learning rates) are also vital considerations.

When might a shallow and wide network be preferable?

In some cases, if the data is relatively simple or you do not have sufficient training data, a shallow wide network can be more practical. It might converge faster, demand fewer hyperparameter tweaks, and be easier to interpret. Additionally, certain tasks that do not require layered abstraction might be adequately handled by a shallow network with enough capacity.

Below are additional follow-up questions

What are some practical debugging steps when a deeper network fails to converge?

One common pitfall with deep networks is that they can appear to “train” (loss might steadily decrease) but never truly converge to a good solution. Alternatively, the loss might not decrease at all. When faced with such issues, there are several practical debugging steps:

1. Examine your data pipeline. Minor data preprocessing mistakes can disproportionately affect deeper networks. Subtle mislabeling or corrupted samples can cause deeper architectures to diverge, especially if the gradient updates amplify small irregularities in data.

2. Start with a smaller subset of data. If the model cannot overfit even a tiny subset of the dataset, there is likely a significant problem (e.g., learning rate too high, incorrect loss calculation, or data loading issues).

3. Reduce the depth or remove some layers. If a shallower version of the network can train properly, reintroduce extra layers incrementally to see which layer(s) introduce instability.

4. Check your initialization. Improperly scaled initial weights can cause gradients to explode or vanish right from the start, derailing training before it even begins.

5. Lower the learning rate. Deeper networks often need smaller learning rates to stabilize gradient updates.

6. Verify gradient flow. Examine the magnitude of gradients at various layers. If the gradient norm is zero or exceedingly large at certain layers, investigate activation functions and try techniques like residual connections or batch normalization.

In real-world scenarios, any one or a combination of these issues might be contributing to the model’s inability to converge. Pinpointing the root cause often requires iterative hypothesis testing and monitoring.

How do you balance computational overhead when comparing deeper vs. wider networks?

Deeper networks can introduce more sequential operations, potentially increasing the training time despite having fewer parameters per layer. Wider layers can similarly escalate parameter counts, leading to substantial memory usage and slower matrix multiplications. Balancing these considerations involves:

• GPU memory constraints. Wider networks with extremely large hidden dimensions can exhaust GPU memory. In contrast, deeper networks might still fit in memory but take longer in terms of sequential compute (depending on architecture). • Parallelization. Modern hardware often benefits from well-optimized matrix operations. Wide matrices can exploit parallelized multiplications but become bottlenecks if too large. Deeper models can be parallelized as well (model or pipeline parallelism), but they can also suffer from overhead if the sequence of layers is too long and not easily split across devices. • Batch sizes. Wider networks may reduce the feasible batch size due to memory constraints, potentially changing the gradient variance dynamics. Deeper networks might allow a larger batch size but require more computational passes. • Inference speed. If you need fast real-time inference, deeper networks might introduce latency because data flows sequentially through more layers. Wider networks might have fewer layers to traverse but more substantial matrix multiplications.

Pitfalls often arise when one neglects to consider real-world hardware limitations or operational constraints. A theoretically ideal network might be infeasible to deploy if inference latency is too high or if memory usage is exorbitant.

Could a shallow, extremely wide network approximate a deep network’s capability?

From a universal approximation viewpoint, shallow networks (with sufficient width and proper activation functions) can theoretically approximate a wide range of functions. The same goes for deep networks. However, several nuances arise:

• Parameter efficiency. A deep model can require fewer overall parameters to approximate certain functions that involve compositional structures. A shallow network might need an exponentially larger number of units to achieve the same complexity. • Training dynamics. Although a shallow wide network might approximate anything in theory, it could be much harder to train in practice because it cannot exploit hierarchical feature extraction. Gradient-based optimization might converge more slowly or get stuck in poor local minima. • Interpretability. A deeper architecture often has intermediate layers that correspond to meaningful features, especially in vision and language tasks, whereas a single wide layer is less interpretable. This difference matters in domains requiring transparency.

Edge cases include certain simple tasks where extreme width and minimal depth can still achieve competitive results, especially if data is plentiful and the function mapping is not inherently hierarchical. But in most real-world scenarios, stacking layers (adding depth) tends to be more efficient.

How does layer normalization or batch normalization help when going deeper?

When networks increase in depth, the distribution of inputs to deeper layers can shift as earlier layers learn, a phenomenon called internal covariate shift. Batch normalization or layer normalization mitigates this by normalizing intermediate activations:

• Smoother optimization landscape. Normalization reduces the sensitivity of deeper layers to changes in earlier layers, promoting more stable gradient flow and faster convergence. • Reduced gradient variance. By enforcing a more standardized distribution, gradients become more consistent across the training set, often allowing higher learning rates and faster training. • Regularization effect. Techniques like batch normalization can act as an implicit regularizer, helping to prevent overfitting in deeper models.

An edge case arises when mini-batch sizes are very small or distribution shifts occur between training and inference. Batch normalization may become less reliable or require careful tuning of running averages. Layer normalization, which normalizes across the neurons in a layer rather than across the batch dimension, often helps in scenarios like natural language processing with variable-length sequences or small batch sizes.

How do dynamic architectures (e.g., skip-layer excitation, gating mechanisms) affect depth-related challenges?

Dynamic architectures, such as those involving gating mechanisms or skip connections that are learned during training, can mitigate some depth-related issues:

• Adaptive gradient flow. Gating can selectively damp or amplify signals passing through layers, helping to avoid vanishing or exploding gradients by dynamically controlling the path of backpropagation. • Task-specific adaptivity. Certain gates might only “open” relevant pathways for subsets of data or tasks, effectively making the network deeper for complex samples and shallower for simpler ones. This can save computation and reduce overfitting. • Potential complexity. While gates and skip connections provide flexibility, they introduce additional complexity in parameter space and hyperparameter tuning. During training, if gates become “stuck,” they might shut off certain layers entirely or remain always open, undermining potential benefits.

A pitfall to watch out for is unanticipated interactions among multiple gating layers. In some real-world scenarios, a gating layer might hamper training if initialized poorly or if the gating function saturates too quickly.

What special considerations are needed for domain-specific architectures (images vs. text vs. tabular data)?

Certain data modalities can favor deeper architectures, whereas others can work well with wide ones:

• Images. Deep CNNs or Vision Transformers leverage hierarchical representation of spatial features—low-level edges, corners, then textures, and so on. This natural hierarchy aligns with depth. Very wide networks may not exploit the spatial locality as efficiently unless combined with specialized convolutional layers. • Text. Transformer-based models rely on multi-head attention layers repeated many times to capture language context. Depth is crucial to integrate semantic information across positions in the sequence. Wider feed-forward blocks can help, but the stacking of attention layers usually brings the biggest representational gains. • Tabular data. Shallow networks or tree-based methods (like XGBoost) can often compete strongly, especially if the feature space is not inherently hierarchical. Depth can still help, but it must be accompanied by robust regularization to prevent overfitting on tabular features. • Audio or time-series data. Recurrent or convolutional filters stacked in depth can capture temporal patterns at multiple scales. Large hidden states (wider) can help store information, but adding layers can also expand representational power across different time segments.

A subtle pitfall is to assume that a deeper approach will always outperform simpler methods. If a data domain has strong structure (like images), deep networks can excel. In more unstructured domains, the improvements might be marginal, not worth the added complexity.

How do you approach hyperparameter tuning differently for deeper versus wider models?

Deeper models and wider models can exhibit different sensitivities to hyperparameters:

• Learning rate. Deeper networks often benefit from lower learning rates to avoid exploding gradients. Wider networks can sometimes tolerate slightly higher learning rates due to fewer sequential transformations per pass. • Regularization strength. Deeper models typically require more regularization (dropout, weight decay) because of their large number of layers. Wider networks might require targeted techniques like specialized dropout patterns to handle the high capacity introduced by wide layers. • Batch size. Deeper models can sometimes train more effectively with moderately sized batches to maintain gradient variability. Wider networks with large parameter counts might demand smaller batches due to GPU memory constraints or might benefit from large batches if hardware permits. • Initialization. Depth amplifies poor initialization. Carefully scaling weights becomes crucial to prevent vanish/explode. Wider networks can also suffer from ill-chosen initial scales, but typically, deeper stack effects are more severe.

Pitfalls often arise when reusing hyperparameters that were successful for a shallow or wide model on a deeper network. Even small differences in initialization or learning rate scheduling can drastically impact deeper architectures.