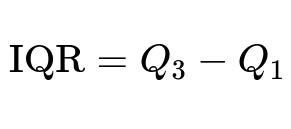ML Interview Q Series: How is the interquartile range (IQR) applied in the setting of time series forecasting?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
The interquartile range (IQR), which is the difference between the 75th percentile (Q3) and the 25th percentile (Q1) of a dataset, is a measure of statistical dispersion. It is robust against outliers and often used to quantify variability or detect unusual data points. In time series forecasting, the IQR proves useful in several ways, such as identifying anomalous observations that may distort model training, or for setting adaptive thresholds that help with forecasting tasks that require dynamic management of variability over time.
One of the main reasons to use IQR in time series contexts is that many traditional measures of spread (for example, standard deviation) are heavily influenced by outliers and may not accurately reflect the true variability of time-dependent data. By relying on the middle 50% of the data points, IQR better captures typical fluctuations. Outliers in time series might be due to real sudden changes (like a genuine shock in demand) or spurious noise (like sensor malfunctions). Employing IQR can help disentangle those two situations.
How IQR is Computed
The IQR is typically computed by subtracting the 25th percentile value from the 75th percentile value of a distribution. This is commonly shown as:
Where Q3 is the 75th percentile (upper quartile), and Q1 is the 25th percentile (lower quartile). For time series forecasting tasks, these quartiles are derived from the historical distribution of the time series values.
Below the formula: Q1 (also called the lower quartile) is the value at the 25th percentile in the sorted data distribution. Q3 (the upper quartile) is the value at the 75th percentile. Their difference (Q3 minus Q1) represents the range of the central 50% of the data.
Outlier Detection in Time Series via IQR
For many practitioners, a common outlier detection rule uses an “IQR multiplier.” Observations lying outside the interval [Q1 - 1.5IQR, Q3 + 1.5IQR] are often considered outliers. In time series, the usage might be adapted to sliding windows or rolling windows:
Use a rolling window of a specific length (for instance, a window of 30 days if you are analyzing daily data) to calculate Q1, Q3, and IQR over that window. Then any newly observed value that falls outside the extended boundary might be labeled an outlier. This approach allows the thresholds to adapt to changes in the data’s distribution over time, which is crucial if your time series is nonstationary or exhibits seasonal effects.
Detecting anomalous values in this manner can improve forecasting performance by either treating those outliers separately (e.g., building a specialized model for outliers) or smoothing them if they are considered noise. This is especially helpful for algorithms that assume normality or that are sensitive to large deviations, such as linear regression-based models.
Impact on Forecasting Model
Using IQR-based outlier management can benefit both the training and prediction stages:
During training, one can remove or reduce the influence of outliers that fall outside a certain IQR-based boundary. That way, the model is not biased by large, one-off deviations.
During prediction, an IQR-based approach to new data can highlight unexpected changes or structural breaks in the time series, prompting you to reevaluate assumptions such as stationarity or seasonal patterns.
Handling Time Series Trends and Seasonality
When applying an IQR-based approach in practical time series settings, be mindful of systematic trends or seasonal effects. If the data has a significant upward or downward trend, raw data might keep drifting outside an IQR-based boundary. To address that, compute quartiles on a detrended series, or use rolling windows that adapt to local distribution changes.
Likewise, if the time series exhibits strong seasonal patterns, you can segment the data by season before computing Q1 and Q3 values to ensure that apples-to-apples comparisons are being made.
Scalability and Efficiency
Computing quartiles in a rolling-window framework can be done using specialized data structures or approximate quantile estimators to handle large-scale data. Libraries in Python (such as pandas or NumPy) offer rolling quantile computations that simplify the process. However, if the time series is huge, more advanced streaming quantile approximations may be necessary.
Code Example: Applying IQR to Detect Outliers in a Time Series
import numpy as np
import pandas as pd
# Example time series data
dates = pd.date_range("2023-01-01", periods=10, freq='D')
values = pd.Series([50, 49, 51, 80, 52, 100, 49, 48, 47, 120]) # intentionally injecting outliers
time_series = pd.DataFrame({"value": values}, index=dates)
# Compute rolling quartiles for a rolling window (e.g., 3 days) for demonstration
window_size = 3
q1 = time_series['value'].rolling(window_size).quantile(0.25)
q3 = time_series['value'].rolling(window_size).quantile(0.75)
iqr = q3 - q1
# Use 1.5 * IQR rule to define the outlier threshold
lower_bound = q1 - 1.5 * iqr
upper_bound = q3 + 1.5 * iqr
# Identify outliers
time_series['LowerBound'] = lower_bound
time_series['UpperBound'] = upper_bound
time_series['Outlier'] = (time_series['value'] < time_series['LowerBound']) | (time_series['value'] > time_series['UpperBound'])
print(time_series)
The code above illustrates how you might detect outliers in a rolling-window context using IQR. Once flagged, you can decide how to handle these points in your forecasting pipeline (e.g., remove them, cap their values, or treat them in a separate modeling approach).
Potential Pitfalls
IQR-based detection might be too conservative or too lenient, depending on the nature of your data. If the data has heavy tails, a factor of 1.5 * IQR might not be sufficient to detect unusual values. Adjusting that multiplier or using robust transformations (like log transforms) may be necessary. Moreover, if the time series is highly volatile, an IQR approach that uses a small rolling window might generate too many false positives. Balancing window size and the multiplier is key to practical usage.
Using IQR for Confidence Intervals
Another interesting application is to use IQR for constructing robust confidence intervals around forecasts. Rather than relying on assumptions of normality, one can store the distribution of residuals from a validation set, calculate the IQR of those residuals, and then define intervals around the forecast. This provides a more robust measure of uncertainty, particularly when residual distributions are skewed or contain outliers.
Follow-up Questions
How do you choose an appropriate rolling window size when calculating IQR in a nonstationary time series?
Choosing a rolling window depends on the domain and the frequency of underlying patterns. If there is a known seasonality of a certain length (for example, 7 days for weekly seasonality), the window should at least span that pattern to capture typical fluctuations. Domain knowledge is often invaluable here. However, if the series changes rapidly (like a dynamic online user behavior metric), shorter windows might be necessary to capture local behavior. One can experiment and compare how the outlier detection impacts the overall forecast error or anomaly detection rates to arrive at an appropriate window.
How do you handle extreme spikes (true anomalies) that are actually important signals rather than data errors?
When a spike or dip in the series is not an artifact but a meaningful event (for instance, a real surge in demand), you might not want to remove it but rather highlight it to the model. Some approaches include marking these events as special features (like adding a binary feature for “spike day” or the magnitude of the spike) or using models that can explicitly account for events (e.g., using Bayesian structural time series with a spike-and-slab prior). Determining whether an anomaly is a genuine event or noise often relies on deeper domain context.
What is the impact of IQR-based outlier handling on model generalization?
If you remove or down-weight real extremes too aggressively, the model may not learn how to handle these rare but important events. Consequently, it may lead to a model that performs well during typical conditions but fails under extreme scenarios. Striking a balance is crucial. Many practitioners rely on robust modeling approaches or hybrid strategies where they fit a model to “normal” data and add specialized anomaly-capturing logic for rare events.
How does one address seasonality when using an IQR-based detection method?
If you suspect seasonal patterns, you can build separate quartile estimates per season. For instance, compute Q1 and Q3 for each hour of the day (if you have hourly data) or each day of the week (if you have daily data) across multiple weeks. That way, you are comparing a data point only with other data points belonging to the same seasonal phase. Alternatively, you can seasonally decompose the series (using classical decomposition or STL), and apply IQR-based detection on the residual component. This effectively removes the predictable seasonal structure before checking for outliers.
How can you apply IQR-based methods in conjunction with machine learning forecasting approaches like LSTM or Transformer-based models?
For deep learning models like LSTMs or Transformers, anomalies can distort learning and cause poor generalization. You can use an IQR-based method to detect and remove or modify anomalous points prior to training, or you can feed an additional anomaly flag feature into the network. When a new point arrives at test time that sits outside the IQR boundary, the model can be aware that this is an unusual input and handle it accordingly, perhaps by switching to a different module or issuing an alert that the input is outside typical ranges.
By customizing the IQR approach to the characteristics of your time series (taking into account trends, seasonality, and cyclical patterns), you can avoid training on misleading data, incorporate real anomalies into your model logic, and improve overall forecast reliability.
Below are additional follow-up questions
How does the IQR-based approach handle rapidly shifting patterns in real-time data streams?
When a time series changes quickly (for instance, due to a sudden policy change, large-scale user adoption, or abrupt shifts in an IoT sensor’s environment), a static IQR bound based on older data may no longer be relevant. One solution is to maintain a rolling or sliding window for computing Q1, Q3, and the IQR, so that the thresholds adapt to the most recent distribution. However, the length of this rolling window becomes crucial. A window that is too long might delay the detection of new behaviors, whereas a window that is too short may fail to capture typical variations and trigger too many false alarms.
Another factor to consider is whether the pattern shifts are permanent or only momentary. If the pattern shifts permanently, you might need to gradually “age out” older data while giving more weight to the newest observations. One real-world pitfall is that if there is a sudden regime change (e.g., a new marketing campaign drastically changes demand), even a rolling IQR might not adapt fast enough; in that case, you could incorporate domain knowledge to reset or re-initialize the rolling window.
Edge cases:
If the distribution changes drastically within a short period, the rolling window IQR may not recognize the shift soon enough and keep flagging legitimate new values as outliers.
If data velocity is extremely high, the computational cost of computing rolling quartiles in real-time might be non-trivial, requiring approximate streaming quantile algorithms to handle large-scale data efficiently.
In what scenarios might IQR not be the most appropriate measure of dispersion for time series outlier detection?
While IQR is robust and widely used, it may not always be the best measure for highly skewed distributions or those with heavy tails. In time series such as financial transactions or web traffic spikes, data might exhibit distributions that are inherently heavy-tailed (for instance, occasional giant spikes in traffic).
If the data is extremely skewed, the 25th and 75th percentiles might still fail to reflect the underlying structure of outliers. Sometimes the median absolute deviation (MAD) or other robust statistics like trimmed means might offer better coverage. Also, if the time series has distinct clusters or multimodal patterns (e.g., day vs. night activity), a single IQR estimate may not capture the variability in each cluster. In such cases, separate IQR estimates for each cluster or a more sophisticated approach might be necessary.
Edge cases:
Data with multiple peaks (bimodal or multimodal) could produce an IQR that is too narrow or too wide, leading to either missing anomalies or over-flagging them.
Times when extreme events are frequent, and the concept of an outlier becomes ambiguous (for instance, repeated extreme values in a cyclical phenomenon).
Can the IQR-based method be used to weigh outliers rather than discarding them?
Yes. Instead of outright removing or ignoring outliers, one can incorporate a weighted scheme where observations that lie far outside the central range receive a smaller weight during model fitting. This approach ensures that outliers do not dominate parameter estimation, but they are still present in the training process for the model to learn from.
In practical implementations (like linear regression or gradient boosting), you can assign observation-specific weights based on how far outside the IQR the data point is. Observations within [Q1, Q3] might be assigned the highest weight, while those progressively outside that range receive diminishing weight. A potential approach is to use a weighting function that decreases smoothly as you move away from the center (e.g., a simple linear decay or a more sophisticated function that tails off).
Edge cases:
If you do not adjust these weights carefully, you might still over-penalize points that are actually valid signals (like real spikes).
A dynamic weighting scheme could be expensive to recompute if your time series is huge or changes quickly, making it computationally expensive for real-time systems.
How do you handle negative or zero values in a time series when applying an IQR-based approach?
In many real-world time series, values can be zero or negative (for instance, certain financial metrics or temperature data below zero). The IQR approach itself does not inherently discriminate against negative or zero values, as it solely depends on the relative positions of Q1, Q3, and the spread. However, if the distribution is largely around high positive values and only rarely dips below zero, negative values might be flagged as outliers too frequently, even if they are legitimate.
A practical fix is to segment data ranges or use transformations (like a log transform for strictly positive data). For negative values, you might shift the series by adding a constant offset to ensure positivity and then apply a log transform. Of course, shifting can obscure some interpretability. Another approach is to apply the IQR methodology directly on the original scale but interpret results carefully, especially if domain knowledge suggests that negative or zero values are normal in certain conditions.
Edge cases:
If zero or negative values are extremely rare, the quartiles might be skewed, causing frequent spurious outlier signals.
If you attempt a log transform on data that includes zero or negative values, the transformation may be undefined or require additional manipulations (like offsetting by a constant).
How do you address missing or incomplete data when calculating IQR in a time series context?
Missing data can disrupt percentile calculations because if you skip or impute them incorrectly, it distorts the quartile estimates. A few strategies include:
Forward or backward filling: For data known to be stable over short intervals, you can fill missing values using the last known observation. This approach might artificially smooth the distribution.
Interpolation: If the time series is continuous, interpolation methods (linear, spline) could approximate the missing values. But be cautious, as over-interpolation can remove important data patterns.
Specialized IQR imputation: You can calculate quartiles based on the observed data only, ignoring missing values, and then treat missing values as separate categories if they occur frequently. This might mean not labeling them outliers but assigning them a special status if missingness is non-random.
Edge cases:
If a significant fraction of values is missing, your sample for computing quartiles may be too small or too unrepresentative of actual behavior, resulting in inaccurate outlier detection.
Certain data might have systematically missing values (e.g., sensor off at certain times), and treating those as outliers can be misleading.
How can you scale the IQR method if the dataset is very large or distributed across multiple servers?
On distributed data systems (like Spark or Hadoop), computing quartiles across partitions can be done with approximate quantile algorithms that use sampling or clever data sketches (like t-digest). Exact percentile computations might be too costly at scale.
One approach is to collect partial summaries from each partition, then merge them to approximate the global quartiles. This summary-based approach helps manage memory and computational overhead. However, approximate algorithms might lead to slight inaccuracies in Q1 or Q3, so the outlier thresholds might differ slightly from an exact calculation. Whether this margin of error is acceptable depends on the application’s tolerance for inaccuracies.
Edge cases:
Extremely skewed or heavy-tailed distributions might degrade the accuracy of approximate quantile algorithms, causing under- or over-estimation of quartiles.
Network or memory constraints can limit the frequency of updates; if your data changes quickly, your quartile estimates might lag behind the current distribution.
What if you want to implement IQR-based outlier detection on multivariate time series?
When dealing with multivariate time series, outliers may occur in a single variable, a subset of variables, or only when considering certain variable combinations (interaction outliers). A univariate IQR approach on each feature separately can catch anomalies in that feature, but it may miss joint anomalies that appear normal in one dimension and extreme in another.
A more advanced approach might involve computing robust measures of spread in a transformed space (e.g., principal components or autoencoder latent space). For example, you could:
Project data onto principal components and compute an IQR-based threshold in each principal component dimension.
Use an autoencoder to learn typical patterns, then analyze reconstruction errors. You might apply an IQR approach to the distribution of reconstruction errors.
Edge cases:
If features vary on different scales, standardizing or normalizing them is often necessary before applying a combined outlier detection approach; otherwise, one feature could dominate the measure of spread.
If the correlation structure is complex, a naive approach may trigger false positives, because an extreme value in one feature might be completely explained by another feature.