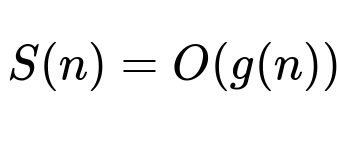ML Interview Q Series: How would you describe what space complexity means, and can you illustrate it with pertinent examples?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Space complexity refers to the amount of memory an algorithm requires to run to completion, aside from the input data. This includes any auxiliary data structures and temporary variables needed for the computation. In many cases, space complexity is indicated using Big-O notation, capturing how the needed memory scales relative to the size of the input.

One formal way to represent space complexity is:

Here, S(n) is the space used by the algorithm for an input of size n, and g(n) expresses the asymptotic upper bound on memory usage. The function g(n) typically depends on factors like arrays, data structures, or recursion overhead that the algorithm employs.

The input itself may also consume memory, but in many analyses, we focus on auxiliary space complexity. This means the memory allocated by the algorithm beyond the space required to hold the input data. For example, if an algorithm sorts a list in place, the space complexity might be referred to as O(1) in an auxiliary sense, even though the actual total memory usage includes the entire list being sorted.

In practical terms, if you implement a sorting algorithm like Merge Sort, you allocate temporary arrays to combine sub-lists, leading to O(n) additional memory usage. Meanwhile, an in-place method such as Quick Sort—depending on the implementation—might achieve O(log n) auxiliary memory due to recursion overhead, which is used for the call stack.

A typical real-world scenario is when you have a large amount of data that you need to process. If an algorithm requires additional memory proportional to n^2, it may be impractical for big n. Efficient space usage can be crucial in memory-constrained systems or for very large input sizes. By controlling the auxiliary data structures, you can reduce overall space requirements and potentially allow algorithms to run faster in systems with limited memory.

Examples

An in-place array reversal algorithm needs only a few temporary variables, so its auxiliary space complexity is O(1). It reads from one end of the array, writes to the other end, and updates pointers or indices in a constant amount of additional space.

A Breadth-First Search (BFS) on a tree or graph often allocates a queue to hold nodes to be visited next. If the graph has V vertices, in the worst case, the queue can hold up to O(V) entries. Here is a simplified BFS implementation in Python to illustrate that extra space usage:

def bfs_traversal(graph, start):
    visited = set()
    queue = []
    queue.append(start)
    visited.add(start)

    while queue:
        node = queue.pop(0)
        # Process node (e.g., print or store it)
        for neighbor in graph[node]:
            if neighbor not in visited:
                visited.add(neighbor)
                queue.append(neighbor)

In this example, the queue data structure grows in proportion to the number of nodes that must be stored at any one time, hence O(V) space in the worst case.

Another common example is storing an adjacency matrix for a graph. An adjacency matrix of a graph with V vertices needs space proportional to V*V to store the presence or absence of edges. An adjacency list, on the other hand, takes space proportional to V + E, where E is the number of edges. The choice between these representations dramatically affects space complexity.

Space complexity also appears in recursive algorithms. For instance, a recursive Depth-First Search (DFS) on a tree-like structure consumes stack memory proportional to the height of the recursion tree. If the recursion depth is n, then the space complexity is O(n).

Why is space complexity different from time complexity?

Time complexity captures how many operations or steps an algorithm requires, while space complexity measures how much additional memory is needed to facilitate the computation. An algorithm can be time-efficient (fewer operations) but can still be memory-intensive if it creates large auxiliary structures. Conversely, some memory-saving strategies might make the algorithm run more slowly, revealing the trade-off between time and space.

When is controlling space complexity more critical?

In real-world high-volume data processing or embedded devices with limited memory, space considerations are paramount. Streaming algorithms that process data as it arrives often have constraints that disallow storing the entire input at once. Minimizing space can be the only way to handle massive data or operate efficiently under strict memory limitations.

What are some pitfalls or edge cases where space complexity plays a major role?

One pitfall is large recursion depth in a naive recursive solution. Deep recursions can overflow the call stack if the input size is very large. Another pitfall is choosing data structures that unintentionally consume more memory than necessary, such as using dictionaries or maps with many empty slots. Also, algorithms that handle sparse data with dense representations (like adjacency matrices for graphs that are mostly empty) can waste a lot of memory.

Could you offer an example of a memory-based trade-off?

Sometimes you can precompute and cache results to reduce computation time at the cost of increased memory usage. For instance, dynamic programming can reduce time complexity significantly by storing intermediate results, but it can require considerable space. This becomes a trade-off decision where you must weigh the benefit of saving on repeated computations against the cost of storing large tables in memory.

How can one reduce space complexity in practice?

One technique is to perform computations in place when possible, using the existing input array or data structure to store intermediate states. Another is to implement iterative solutions instead of recursive ones to avoid excessive call-stack usage. Choosing the right data structure (e.g., adjacency list vs adjacency matrix for sparse graphs) also helps. Garbage collection in high-level languages can mitigate but not eliminate concerns, as any allocated memory is still subject to constraints and overhead.

Careful analysis and design of the algorithm’s data structures, along with an understanding of how memory scales, can ensure that memory usage remains manageable even as input sizes grow large.

Below are additional follow-up questions

What happens if the space complexity includes memory required for storing the input itself?

When we talk about space complexity, we often distinguish between total space complexity (which includes space for the input) and auxiliary space complexity (which excludes the input’s own memory). If an algorithm receives a massive input, storing that data alone might be significant. For instance, if you have an algorithm that must read data from a huge file into memory before processing, the total space usage could be large simply because of how you are handling the input.

A subtle issue is that sometimes you do not need to load all input data at once. You might process it in chunks or use a streaming approach, thereby reducing memory usage. Conversely, if you require random access to the entire dataset in memory for faster computation, you accept a larger total space footprint. The pitfall here is to assume the input data is negligible when, in some cases, it is actually the dominating factor in memory usage. This can lead to unrealistic assumptions in algorithm analysis.

How does space complexity relate to memory fragmentation in practical systems?

Although traditional space-complexity analysis treats memory as an abstract continuous block, in real systems memory might be fragmented, and the operating system must allocate memory in discrete chunks. Even if your algorithm has a theoretical O(1) auxiliary space usage, continuous allocation and deallocation of small data structures can create fragmentation problems over time, especially in long-running processes or in memory-constrained environments.

A subtle real-world scenario is when dynamic allocations (e.g., in a language like C++ where you constantly allocate and free memory) cause fragmentation that results in performance degradation, despite the nominal space complexity remaining low. Garbage-collected languages such as Python or Java do their own memory management, but they can still suffer from overhead if short-lived objects are created in large volumes. This difference highlights that theoretical space usage does not always translate directly to practical memory behavior.

Can an algorithm’s space usage spike during intermediate steps and then go back down?

Yes, some algorithms create large temporary structures in intermediate steps, then discard them. This behavior can temporarily increase peak memory usage even if the final auxiliary space ends up smaller. For example, consider a divide-and-conquer approach that spawns multiple subproblems concurrently. At certain points, you could have many partial data structures in memory at once before combining their results. Once the partial results are merged, memory can be freed or reclaimed.

The subtlety here is that if you only track final space usage, you might overlook the fact that the algorithm hits a higher memory peak during intermediate stages. Real-world systems with limited available memory might fail if the intermediate peak exceeds system capacity. It is important to measure both the maximum simultaneous memory used (peak space) and the total or final auxiliary space when analyzing feasibility on large inputs.

Why might an algorithm with lower time complexity still be rejected if it requires large space?

There are situations where memory or disk storage constraints are the strictest limitations, particularly in embedded devices or large-scale computing clusters. An algorithm that runs in O(n) time but O(n^2) space may be impossible to deploy if the system cannot allocate enough memory or if doing so would disrupt other critical processes. Even if it finishes quickly once all memory is allocated, the overhead of resource setup, the risk of memory exhaustion, or the cost of disk swapping can outweigh any time advantage.

A subtle example arises in data center operations, where multiple processes run concurrently. If your algorithm demands large dedicated memory, it might starve other processes or require special scheduling. This leads to practical engineering trade-offs: sometimes a slightly slower solution that uses much less memory is far more viable in production systems.

How do you analyze space complexity for algorithms that use external storage (e.g., disk or network streaming)?

When dealing with very large datasets, an algorithm might offload part of the computation or partial data to disk or across a distributed storage system. The memory usage in RAM might be O(1) or O(log n) because you only store a small buffer or index in memory at any given time. However, disk usage could be O(n) or larger.

In streaming or distributed computing frameworks (like MapReduce or Spark), space usage includes local memory buffers, shuffle data stored on disk, and the overhead of serialization. Real-world pitfalls arise if your partitioning strategy results in data skew, where one node must handle more data than intended. Even though the overall space usage might be balanced in theory, hot spots can exceed memory limits on particular nodes.

Are there situations where intentionally increasing space complexity can reduce overall resource usage?

Yes, caching (memoization) and precomputation can help avoid expensive repeated operations, thus improving time performance. The trade-off is increased memory usage. For instance, an algorithm that calculates Fibonacci numbers naively uses exponential time with O(n) space due to recursion depth. If you implement a dynamic programming table, you reduce time to O(n) but consume O(n) space. This additional memory can be beneficial if you repeatedly query Fibonacci values.

A subtle real-world example is caching database queries. By storing results in memory, you reduce the load on the database, leading to quicker response times for repeated queries. But the cache might grow large, so you need eviction policies to manage space effectively. The pitfall is that if you let the cache grow uncontrollably, you risk out-of-memory errors or high garbage collection overhead in a managed runtime environment.

What unique concerns arise when analyzing space complexity for parallel or concurrent algorithms?

In parallel algorithms, different threads or processes might each hold copies of data or partial states. Communication overhead can create extra buffers for data exchange. Locks or synchronization mechanisms can also add hidden memory overhead if you use data structures like queues or concurrency-friendly containers.

An edge case occurs when multiple threads each attempt to reserve memory for their local computations simultaneously. Even if each thread’s usage is modest, the aggregate can surpass the available capacity. In GPU-based deep learning, for example, each training batch must fit in GPU memory. If your parallel algorithm spawns multiple GPU kernels concurrently, you can exceed the memory limit and cause training to fail. Therefore, you must carefully plan concurrency so that the total space footprint across all workers is within system limits.