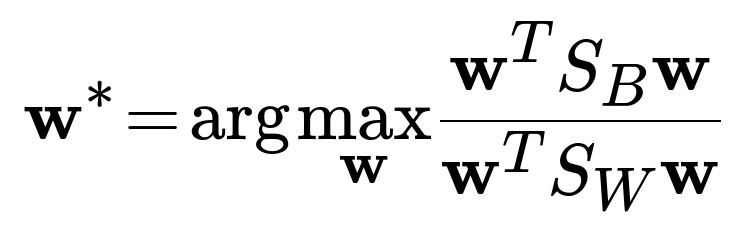ML Interview Q Series: How would you describe the core principle behind Linear Discriminant Analysis (LDA) and what are some scenarios where LDA is applied in real-world practice?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Linear Discriminant Analysis (LDA) is a classical algorithm in machine learning that seeks to find a linear combination of input features that best separates multiple classes. It does so by maximizing the ratio of between-class variance to within-class variance, thereby attempting to project data onto a lower-dimensional subspace where class separability is enhanced.
One of the most central formulas in LDA is where we identify a projection vector w that maximizes the separation between classes. This can be written as:
Here w is the projection vector (in plain text, w is a vector in R^d if we have d-dimensional data). S_B is the between-class scatter matrix, which measures how separated the different class means are from the overall mean. S_W is the within-class scatter matrix, which measures how much the samples of each class differ within that class. The ratio quantifies how well we can find a direction (vector w) that maximizes class separation. In practice, one typically solves this optimization by computing inverse(S_W)*S_B and finding eigenvalues and eigenvectors.
LDA assumes data from each class is generated by a Gaussian distribution with a shared covariance matrix but different class means. This implies that within each class, the data is somewhat normally distributed, and across classes, there is only a shift in the mean. In addition, LDA often serves as both a dimensionality reduction tool and a classifier. When used as a classifier, LDA fits a Gaussian distribution per class and assigns new points to the class with the highest posterior probability.
There are several ways to apply LDA in practice. It can be used for classification when the classes are fairly well separated by linear boundaries, such as in certain medical data analyses, text classification for topic prediction when classes are linearly separable in a feature space, or in combination with other algorithms (e.g., as a dimensionality reduction step before another classifier).
It is also worth noting that LDA, unlike Principal Component Analysis (PCA), takes label information into account. While PCA focuses on capturing the directions of maximal variance in the data overall (ignoring labels), LDA specifically aims to find directions that separate one labeled class from another.
When dealing with multiple classes, LDA finds multiple projection directions. Specifically, with k classes, LDA can produce up to k - 1 meaningful discriminant directions, because that is the maximum rank of the between-class scatter matrix.
Below is a simple Python snippet to illustrate how to use LDA for dimensionality reduction and classification using scikit-learn:
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score
# Example dataset
data = load_iris()
X = data.data
y = data.target
# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Create LDA model
lda = LinearDiscriminantAnalysis(n_components=2)
# Fit LDA model
lda.fit(X_train, y_train)
# Project the data to lower dimensional space
X_train_lda = lda.transform(X_train)
X_test_lda = lda.transform(X_test)
# Predict on test set
y_pred = lda.predict(X_test)
print("Accuracy:", accuracy_score(y_test, y_pred))
What are the assumptions behind LDA?
LDA assumes that each class is generated from a Gaussian distribution that has the same covariance matrix but a different mean vector for each class. This implies that the correlation structure of each class is the same, although the distributions are centered on different means. If the real data deviates significantly from this assumption—particularly if covariances differ across classes—LDA’s performance can degrade. Another assumption is that there are no strong outliers that could dominate the scatter matrices.
When is LDA preferable to PCA?
PCA is unsupervised; it only looks for directions that explain the most variance in the dataset, without considering class labels. LDA, on the other hand, is supervised and aims to find directions that best separate the labeled classes. If one’s goal is classification, especially when the data appears to be (roughly) linearly separable and matches LDA’s assumptions, LDA can be more effective in reducing dimensionality in a class-discriminative way.
How does LDA handle multiple classes?
LDA uses the concept of between-class scatter, which accounts for the difference between each class mean and the overall mean, and within-class scatter, which measures how variable each class is around its own mean. For k classes, LDA can produce at most k-1 discriminative directions. Each direction maximizes separability along a specific linear axis. The model then projects data into the resulting subspace, and classification can be performed by modeling the data in that reduced subspace.
What if the data is not linearly separable?
If the data is not linearly separable or if the assumptions of LDA regarding class covariance structures do not hold, standard LDA may not perform well. One might explore Quadratic Discriminant Analysis (QDA), which allows distinct covariance matrices for each class. Alternatively, more flexible models such as neural networks, kernel-based methods, or ensemble methods like random forests can be used. Kernel LDA is also an option, where the idea of LDA is extended to a high-dimensional feature space induced by a kernel function, allowing non-linear boundaries.
Could LDA still work if classes have vastly different covariance matrices?
Classical LDA is not ideally suited to situations where different classes exhibit significantly different covariance structures. In such cases, Quadratic Discriminant Analysis can be a better fit, because it models each class with its own covariance matrix. If the covariance matrices are significantly different and not well-approximated by a single shared covariance matrix, LDA may yield suboptimal classification.
What are common pitfalls when applying LDA in practice?
One major pitfall is ignoring the assumptions of the algorithm, particularly the assumption that class covariances are similar. Another frequent issue is using LDA on datasets with very high dimensionality but limited training samples. In such situations, the within-class scatter matrix can become nearly singular (because it might be a high-dimensional matrix estimated from insufficient data), leading to numerical instabilities. Regularized LDA or dimensionality reduction before LDA can sometimes alleviate these issues. Additionally, if outliers exist, they can distort the means and scatter estimates, negatively impacting the performance of LDA.
How does one interpret the results of an LDA model?
LDA can be inspected through the linear discriminant directions that it identifies. These directions are essentially weighted combinations of features that maximize separation among classes. By examining the coefficients of these directions, one can infer which features are most influential in discriminating among the classes. If you only extract one or two LDA dimensions, you can often plot the transformed data to visually inspect how well classes are separated.
How could LDA be used in text classification or natural language processing?
When dealing with bag-of-words or TF-IDF features in text classification tasks, LDA can project the high-dimensional text vectors onto lower dimensions while attempting to preserve class discrimination (for example, topic classes). It can help reduce dimensionality from thousands of features to a much smaller number, typically improving computational efficiency and providing insight into the most discriminative words or features. However, in modern NLP contexts, especially with deep learning, this classical LDA approach has largely been supplanted by neural embeddings. Still, LDA might be a viable baseline for simpler text classification tasks when data is limited and the dimensionality is high.
Why do we get at most k - 1 discriminant directions in multi-class LDA?
The rank of the between-class scatter matrix is limited by the number of distinct classes minus one, because each class contributes only one mean vector, and the overall mean can reduce the effective degrees of freedom by one. Thus, the maximum number of meaningful orthogonal directions that separate the classes is k - 1. Once you have those k - 1 directions, additional dimensions do not provide further linearly independent separation.
Could LDA be used primarily as a feature extraction method?
Yes, many practitioners use LDA for dimensionality reduction before feeding the transformed data to another classifier. By projecting data onto the space that maximizes class separation, one can reduce feature dimensionality while retaining strong discriminative power. This helps in speeding up training for subsequent classifiers. However, if the real-world data is highly non-linear, other forms of dimensionality reduction or more flexible classifiers may be more effective.
Below are additional follow-up questions
How can LDA handle missing data?
When dealing with missing data, a typical approach is to impute the missing values before fitting an LDA model. Imputation can be done in various ways, such as mean imputation (replacing missing values with the mean of observed values), median imputation, using k-Nearest Neighbors (k-NN) imputation, or more advanced methods like iterative multivariate imputation. The pitfall here is that imputation can bias the estimates of the mean and covariance if the mechanism behind missingness is not random. LDA relies on accurate estimates of within-class scatter (the covariance) and between-class means, so any systematic distortion introduced by poor imputation methods can significantly degrade the performance of the classifier. In real-world datasets, one must also consider if data is missing completely at random, missing at random, or missing not at random, as this impacts whether a specific imputation strategy is valid.
In extreme cases where a large fraction of values are missing for certain features or samples, it might be preferable to drop those features or samples if it preserves data quality. Alternatively, domain knowledge can guide which features are crucial for classification and which can be safely excluded.
How does LDA deal with class imbalance?
LDA inherently models each class with the assumption of equal covariance but different means. If the dataset is highly imbalanced, LDA may struggle because the within-class scatter matrix is dominated by the majority class, and the mean of a minority class might be less accurately estimated if there are too few samples. One strategy is to incorporate class priors that reflect the real-world distribution or the desired emphasis on minority classes. In scikit-learn, for example, when you instantiate LinearDiscriminantAnalysis, you can specify the parameter priors. By adjusting these priors, LDA’s decision boundaries shift to address imbalanced data better.
However, if the imbalance is extreme, even adjusting priors might not be enough because LDA requires a fairly robust estimate of covariance from each class. In that scenario, one might combine LDA with oversampling (e.g., SMOTE) or undersampling strategies to rebalance the classes. Another potential issue is that the small number of minority-class samples makes the covariance estimate unreliable. Regularized LDA approaches or dimension reduction before LDA can help mitigate this.
What is the computational complexity of LDA and how does it scale?
The computational complexity of LDA primarily comes from estimating the covariance matrix for all samples pooled across classes. Specifically, it involves operations like matrix inversion of the within-class scatter matrix. If the data matrix is of size n (number of samples) by d (number of features), forming and inverting the d x d covariance matrix can be costly when d is large. The complexity often hovers around O(d^3) for naive matrix inversion, plus some overhead from computing the scatter matrices.
In high-dimensional scenarios (d much larger than n), the within-class scatter matrix can be nearly singular, causing numerical instability. Practitioners often resort to methods like Regularized Discriminant Analysis, shrinkage estimators for covariance, or dimensionality reduction (e.g., PCA) prior to LDA to reduce d. These approaches can help maintain both numerical stability and computational feasibility. In big-data contexts with millions of samples, the matrix operations can still be done but might require efficient linear algebra libraries or distributed computing solutions to handle the scale.
Can LDA be applied incrementally to streaming data?
Classical LDA is a batch algorithm that relies on computing scatter matrices over the entire dataset. For streaming data, you would need to update class means and covariance estimates incrementally. While incremental versions of LDA are less common in off-the-shelf libraries, it is possible in theory to maintain running estimates of class means and scatter matrices using incremental statistical formulas. The difficulty lies in updating the inverse of the within-class scatter matrix (or a similar quantity) in an online fashion.
An edge case is when classes evolve over time, meaning their statistical properties drift. If distributions shift significantly, then the historical estimates of class means and covariance structures may no longer be valid. This scenario would require a mechanism to detect concept drift and reset or adapt the LDA model accordingly. Consequently, for streaming data or data with distribution shifts, other adaptive or online learning methods might be more appropriate.
How do we interpret the discriminant axes when features are correlated?
When features are highly correlated, the covariance matrix of the pooled data might exhibit near-collinearity. In LDA, the linear discriminant directions are essentially eigenvectors of the product inverse(S_W)*S_B. If strong correlation exists, the directions that maximize between-class variability relative to within-class variability could emphasize subtle differences that might be hard to interpret in the original feature space. You might see large positive or negative coefficients on certain highly correlated features.
To interpret these directions, one should look at the weights assigned to each original feature in the discriminant axis. A high magnitude weight indicates a strong influence in determining class separation along that axis. However, if multiple features carry redundant information (due to correlation), interpretability can be tricky—small changes in correlated features can lead to big shifts in the projected space. A typical practice is to check a correlation matrix or variance inflation factors before applying LDA and consider dimension reduction or regularization if correlation is too high.
What is the difference between LDA used in classical machine learning and “LDA” in topic modeling?
The acronym LDA can refer to two distinct methods:
Linear Discriminant Analysis (LDA): A supervised learning technique for classification and dimensionality reduction that relies on maximizing between-class variance relative to within-class variance.
Latent Dirichlet Allocation (LDA): An unsupervised probabilistic model for topic discovery in text documents.
These methods share the same acronym but are conceptually different. Linear Discriminant Analysis works with labeled data, whereas Latent Dirichlet Allocation deals with unlabeled text corpora and tries to discover latent topics. Their underlying assumptions, formulations, and applications differ significantly. One pitfall in real-world discussions is mixing them up if the context is not clearly stated.
Are there limitations on the number of features relative to the number of samples?
LDA requires estimating the covariance matrix for each class (or a common covariance for all classes). This estimation is only reliable if the number of samples n is significantly larger than the number of features d. A rough rule of thumb is that you need at least 10 to 20 times as many samples as features to get a stable covariance matrix estimate. If d is comparable to or larger than n, the within-class scatter matrix can become singular (non-invertible).
A practical workaround is to apply dimensionality reduction before LDA or use a regularized version of LDA (e.g., shrinkage LDA), which helps stabilize estimates of the covariance matrix in high-dimensional, low-sample-size regimes. Another approach is to exclude features that provide little variance or are highly correlated, though one should be careful not to remove potentially important discriminative information.
How can one evaluate whether LDA’s assumptions hold true in practice?
LDA assumes multivariate normal distributions for each class with a shared covariance matrix. While strict normality is often not met in real-world datasets, the method remains robust if data is “reasonably” elliptical or if no extreme deviations exist. You can perform checks such as:
Inspecting histograms, Q-Q plots, or kernel density estimates of each feature per class to see if the distribution is approximately normal.
Estimating and comparing covariance matrices for each class to see how different they are. If they differ widely, you might suspect LDA’s assumptions are violated.
Looking for heavy tails or outliers in your data, as outliers can distort the mean and covariance estimates.
In practice, if you find strong violations of normality or large differences in covariance, you might use Quadratic Discriminant Analysis (QDA) or non-linear methods.
Can LDA handle multi-label classification?
LDA is generally used for multi-class (single-label) classification, meaning each sample belongs to exactly one of several classes. Multi-label classification, where each sample can belong to multiple classes simultaneously, is not natively supported by standard LDA. One workaround could be to train multiple one-vs-rest LDA classifiers (one for each label), but this does not fully capture correlations between labels. If label interdependencies are critical, a different family of methods (e.g., neural networks with sigmoid outputs or specialized multi-label algorithms) is more suitable. A pitfall of forcing LDA into multi-label tasks is the assumption that each sample belongs to only one Gaussian distribution with a single mean vector, which breaks down when multiple labels apply.
Is LDA suitable for high-dimensional domains like image classification?
While LDA can be applied to image data, such tasks often have extremely high dimensional features (pixels) and complex class boundaries that are not well described by a single linear projection. Moreover, images rarely follow a simple Gaussian distribution with a shared covariance structure across classes. If you still want to try LDA, you might first apply dimension reduction (e.g., PCA or an autoencoder) to reduce the image dimensionality. Then LDA could be used either as a final classifier or to extract additional discriminative axes after the initial reduction.
One must be aware that high correlations among pixels and the generally non-linear manifolds on which images lie can degrade LDA’s effectiveness. Deep learning techniques typically outperform LDA in image-based tasks, though LDA might be acceptable for simpler image classification tasks with moderate resolution and well-defined class boundaries.
How can we incorporate domain knowledge into LDA?
Although LDA is generally a straightforward statistical method without built-in hooks for domain knowledge, you can indirectly incorporate domain knowledge by:
Engineering relevant features or selecting features that are known to be discriminative based on domain expertise.
Applying domain-specific transformations or normalizations to ensure that features follow roughly normal distributions.
Adjusting class priors if you know the relative importance or prevalence of different classes, which influences the posterior probabilities and, thus, the decision boundaries.
An edge case is when domain knowledge suggests that the covariance structure should differ by subgroups within the same labeled class. LDA won’t capture that. You might need more specialized methods, hierarchical classification strategies, or ensemble approaches that take domain structure into account.
What are possible strategies if LDA decision boundaries are too strict?
Because LDA uses linear decision boundaries derived from a single shared covariance estimate and different means, these boundaries can be too rigid if classes overlap non-linearly. Strategies to address this include:
Kernel LDA: Map data to a higher-dimensional feature space via a kernel function. The method then attempts to find a linear discriminant in that space, which corresponds to a non-linear discriminant in the original space.
Quadratic Discriminant Analysis (QDA): Allows each class to have its own covariance matrix, yielding quadratic decision boundaries.
Ensemble or other non-linear methods: Methods like random forests or gradient-boosted decision trees can often capture complex decision boundaries better.
Each approach has trade-offs. Kernel LDA can be computationally expensive for large datasets. QDA can overfit if you do not have enough data per class to reliably estimate separate covariance matrices. Non-linear ensemble methods often require careful tuning and may lose the interpretability that LDA provides.
How do we tune hyperparameters in LDA?
Classical LDA doesn’t have many hyperparameters beyond possibly setting priors or specifying a regularization parameter in “shrinkage” versions. In scikit-learn, for instance, you can set shrinkage='auto' to apply Ledoit-Wolf shrinkage automatically. This can improve performance in cases of high dimensionality or small sample size. If your library supports specifying manual shrinkage strength, you can select an optimal value via cross-validation.
Another consideration is how many components to retain. If you are using LDA purely for dimensionality reduction, you can choose up to k - 1 components, where k is the number of classes. In a multi-class setting, you can experiment with using fewer than k - 1 components if that suffices for good discrimination and if interpretability or computational efficiency is prioritized.
How do outliers specifically distort LDA?
Outliers can heavily shift the mean of a class and inflate the within-class scatter matrix, both of which degrade LDA’s ability to find a good projection. Because LDA relies on the sample mean and covariance, a single extreme point might warp the direction that maximizes between-class separation. If you suspect outliers, you can:
Apply robust scaling or transformations (e.g., log transform) to features prone to outliers.
Use robust statistics like median-based estimates for preliminary checks.
Filter out obvious anomalies based on domain knowledge.
However, automatic removal of outliers can also remove valid “rare” data points essential for certain classes. Careful analysis is needed to decide whether an outlier is an erroneous measurement or a legitimate—though less frequent—instance of the data distribution.
Does LDA work well for time-series data?
Time-series data typically exhibits autocorrelation and temporal dynamics that LDA does not explicitly handle. If you attempt to use LDA directly on raw time steps, you may miss temporal relationships. One workaround is to extract summary features (e.g., mean, variance, or features derived from a window of time) and then apply LDA to those summary features. Still, if the classes evolve over time, or if time-lags and seasonality are key factors, a purely static model like LDA is suboptimal. Models that handle temporal structure, such as Hidden Markov Models, LSTM networks, or other specialized architectures, might provide better performance.
LDA can still be useful in time-series classification if the domain knowledge allows you to transform the data into a static feature vector that captures the discriminative characteristics of each class. But you have to be sure that a linear separation in that feature space is relevant to your classification goal.