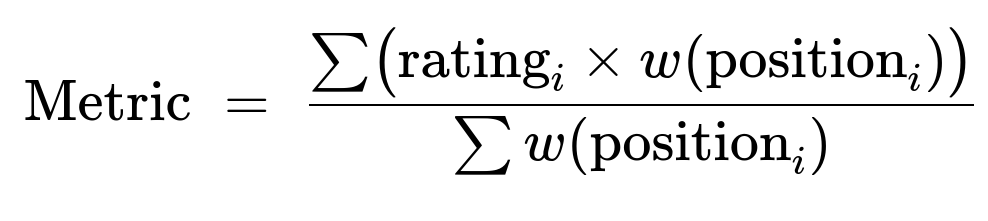ML Interview Q Series: How would you compute a precision metric to evaluate if higher-rated results appear in earlier positions?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
One way to interpret this question is to find a measure of how well the results are ordered based on their ratings. If the ratings are high, we want those results to appear in earlier positions. While there are many possible metrics (e.g. correlation-based, average precision, or various weighting schemes), an accessible and straightforward approach is to compute a “weighted average” of the ratings that penalizes results with high relevance but poor placement.
Below is one conceptual way to do it:
• We first note that each search result has a position (1, 2, 3, …) and a rating (1 to 5). • Since a search result at position=1 is generally more important than a search result at position=5, we can weight each rating by some function of its position. A simple choice is to give higher weight for earlier positions. • Finally, we compute a weighted average that captures “Does the ranking system place high ratings in early slots?”
Example Metric: Weighted Average Rating
A simple weighted scheme could be:
Where rating_i is the rating of the i-th result, and w(position_i) is a weight function that decreases as position_i grows. For instance, w(position) = (constant - position + 1) or 1/position, or even a logarithmic function. Different weight choices yield different behavior, but all try to reward a search result that has high ratings in high-priority (i.e. early) positions.
If we choose w(position) = 6 - position for a small set of positions (like 1 through 5), then position=1 receives a weight of 5, while position=5 receives a weight of 1. If a row has rating=5 in position=1, it contributes 25 in the numerator. If a row has rating=5 in position=5, it only contributes 5 in the numerator, and so on. Though simplistic, it is easy to grasp and works decently if your position range is limited.
Creating a SQL Query
Suppose the table is named search_results and has columns:
query(text)position(integer)rating(integer, from 1 to 5)
A potential weighted-average query in many SQL dialects could be:
SELECT
query,
ROUND(
SUM(rating * (6 - position)) * 1.0
/ SUM(6 - position)
, 2
) AS avg_rating
FROM
search_results
GROUP BY
query
ORDER BY
avg_rating DESC;
Explanation of this query:
• SUM(rating * (6 - position)) is summing up each result’s rating multiplied by the weight (6 - position). • SUM(6 - position) sums all the weights for that query. • Dividing the weighted rating sum by the sum of weights gives a weighted average. • Multiplying by 1.0 (or casting to float) ensures floating-point division in some SQL engines. • ROUND(..., 2) rounds the result to 2 decimal places as required. • We then group by the query because we want a separate metric per query. • Finally, ordering by avg_rating DESC ranks queries from highest “precision” metric to lowest.
Why This Works for Ranking Precision
This metric punishes cases where highly rated results show up at low (later) positions by giving them smaller weight. Conversely, if all the results with rating=5 appear at the earliest positions, the sum of rating*weight is quite high, which boosts the average. An alternative could be to use more established IR (Information Retrieval) metrics like DCG/NDCG, but the above captures the essence of “Is the rating aligned with the position?” in a simpler form.
Handling Edge Cases
• If a query returns no results, then obviously no metric is computed. • If a query returns more than five positions, you can adapt the function 6 - position into something that accommodates the extended positions (e.g. 101 - position for up to 100 results). • If two or more results have the same rating, the order among them won’t matter much to this particular formula, but alternative metrics might differentiate them based on additional signals.
Potential Follow-up Questions
How would you adapt this if there are many more than 5 positions?
Weights like (6 - position) might be too simplistic if a query returns 50 or 100 results. You could make w(position) a function that smoothly decreases over more positions:
– A typical approach is w(position) = 1 / position or 1 / log(position + 1). – Another widely used ranking metric in IR is the Discounted Cumulative Gain (DCG) which uses a logarithmic discount: rating_i is often transformed to 2^(rating_i) - 1, and the discount factor is log2(position_i + 1).
What if the data has ties in ratings or missing ratings?
When multiple results for the same query have the same rating:
– The formula above still works: if they are all rating=4, each row simply contributes 4 * w(position). – However, if we want to truly measure “correctness of sorting,” we might use a rank-correlation measure such as Spearman’s or Kendall’s correlation. This compares the ideal rank ordering (descending by rating) to the actual position ordering, producing 1 for a perfect correlation and -1 for perfect disagreement.
If some entries do not have a rating (null values), one could either discard them or treat them as rating=0, depending on the business logic for “unrated.”
How would you validate this metric in real-world scenarios?
You might:
– Compare the metric’s ranking results against user-engagement signals (e.g. click-through rates). – Check how the metric correlates with known user satisfaction data. – Conduct A/B tests where you slightly alter the ranking and measure changes in user behavior versus the metric’s predictions.
Could we compute more advanced metrics like NDCG in SQL?
Yes, though it can be more involved:
– You would rank each result by actual position, compute DCG = sum of (2^(rating) - 1)/log2(position+1). – Then compute the ideal DCG by sorting ratings in descending order (i.e. best rating first) and summing the same formula. – NDCG is DCG/IDCG. In SQL, you would likely use window functions to implement these steps. – Rounding can be applied at the final stage similarly with ROUND(…, 2).
Such metrics provide a more standard IR-based approach for analyzing ranking performance. But the principle remains: measure how well the system places higher ratings in top positions, penalizing misplacements in deeper results pages.
Below are additional follow-up questions
How would you handle cases where the number of returned results can vary significantly across different queries?
When some queries yield only a handful of results (e.g., 2 or 3 items) while others return dozens or hundreds, the metric may be biased toward queries with fewer results. A query with fewer results may trivially have a perfect arrangement, but that might not be as meaningful as consistently ranking multiple items correctly for a bigger query.
One way to address this is to incorporate a normalization term that accounts for the number of items in each query. For instance, you could ensure the weighted average or DCG computations are normalized by the maximum possible score for that specific number of results. Alternatively, you can only compute the metric for queries above a certain result count threshold to ensure fair comparisons. Another subtle point is that queries returning a large number of items may not have consistent user intent throughout all positions (users might not scroll beyond the first page), so the weighting scheme might heavily discount results beyond, say, position 10 or 20 to align with typical user behavior.
Potential pitfalls include deciding a suitable cutoff for positions, deciding how to compare queries with extremely short or extremely long result sets, and capturing partial user engagement (like users who only ever check top 3 positions). All of these factors could influence how the metric is interpreted in real-world settings.
What if the ratings come from different human raters with varying levels of strictness?
Human raters might systematically differ in how they assign a rating. One rater might rarely give a rating of 5, while another might be more generous. This variation can skew the metric if, for example, the first rater handles primarily “cat” queries and the second rater mostly handles “dog” queries. If you directly compare these metrics without calibrating or normalizing across raters, you might incorrectly conclude that one query’s ranking is inferior or superior.
To handle this, you can introduce a rater calibration step—often involving statistical techniques like z-score normalization or anchor tasks (common items rated by multiple raters). You can also track rater ID and factor it into your data processing, so that each rater’s bias is corrected before aggregating ratings. A potential pitfall is ignoring such variations and naively comparing queries, which can systematically under- or over-represent certain query categories rated by stricter or more lenient evaluators.
How would you deal with rapidly changing user intent or seasonality effects in the ratings?
Over time, certain queries may exhibit seasonal patterns (e.g., “tax returns” might spike around tax season) and the relevance of certain results might shift. A metric computed across a large time window could obscure short-term changes in user intent. For example, a product that was highly relevant last month might no longer be relevant today.
To tackle this, you could:
• Segment your metric calculations by time intervals (weekly or monthly) to see trends. • Apply time-based weighting, favoring more recent ratings. • Compare “latest period performance” vs. “historical performance” to see if the ranking system is adapting quickly.
Pitfalls include ignoring these seasonality effects and letting stale or outdated ratings skew your current performance assessment. Similarly, choosing the wrong time window might either discard too much data or dilute recent trends.
Could we incorporate user behavior signals (e.g., clicks, dwell time) directly into this ranking precision metric?
Yes. While human ratings are invaluable, actual user interactions (clicks, dwell time, bounce rate) often reveal a more direct measure of perceived relevance. You might replace or augment the human rating field with a user-engagement-based score. For instance, a search result that yields a high click-through rate and a long dwell time could be considered more relevant than one with fewer clicks or quick bounces.
Implementation details could include:
• Defining a “quality score” for each result that combines rating and user engagement. • Creating a logistic model or a heuristic that transforms click/dwell metrics into a numerical relevance measure. • Ensuring you distinguish between position bias (earlier positions usually get more clicks) and genuine relevance.
A subtlety here is that user behavior is itself influenced by the ranking. High positions get more clicks simply because they’re at the top. One pitfall is to mistakenly treat clicks as an unbiased signal of relevance without correcting for position bias. This might incorrectly reinforce the existing ranking, limiting improvements or alternative ranking strategies.
In what scenarios might a perfect average rating not necessarily indicate a good user experience?
Even if a query has consistently high ratings in the top positions, there are situations where user experience may still be suboptimal. For instance:
• Diversity of results: If a user searches for “dog,” an ideal set of results might cover a broad range of dog-related content (breed info, training tips, local dog parks, etc.). A set of results that are all rated 5 but focus on only one aspect (e.g., images of dogs) may not truly satisfy varied user intent. • Timeliness: A high rating might reflect historical relevance, but if the user is looking for current or breaking news, old results—even if rated 5—may be out of date. • Context changes: Some queries are ambiguous or multi-intent (like “apple,” which could refer to the company or the fruit), and a single dimension rating may not capture the need for multiple relevant results for different interpretations.
Hence, a uniform 5 rating does not guarantee that you have actually satisfied all possible user needs. One pitfall is focusing purely on numeric ratings while ignoring diversity, freshness, or multi-intent search scenarios.
How would you handle large-scale performance and data-processing challenges when computing these metrics for billions of queries?
When the dataset becomes massive, you might face:
• Computational complexity: A naive approach that scans every row for every query can be extremely time-consuming, especially if you have billions of rows. • Data distribution: Queries may have a heavily skewed distribution (a small number of queries might account for a huge fraction of searches).
Mitigations could include:
• Building an aggregated or partitioned system (like a data pipeline on Spark or BigQuery) to compute partial aggregates, then reducing them. • Using approximate queries, sampling, or summary tables to reduce data size. • Considering real-time or near-real-time pipelines that update metrics incrementally instead of batch-computing from scratch.
Potential pitfalls include introducing sampling biases if the data sample is not representative, dealing with highly skewed distributions (some queries have huge volumes of data while others have almost none), or losing timely insights if batch jobs are slow or infrequent.
How would you respond if the business decides to adjust relevance ratings for specific strategic objectives (e.g., promoting new products or content)?
Sometimes business logic dictates that certain items should be artificially promoted or demoted, regardless of their “organic” rating. This can create a mismatch between your rating-based precision metric and actual system rankings.
You could handle this by:
• Separating “organic” metrics from “boosted” metrics. If certain search results are promoted artificially, you might track a separate set of metrics for them. • Adjusting your metric calculations to label or exclude artificially boosted results, so you don’t penalize the system for something that is intentionally done by business policy. • Conducting A/B tests to see how these strategic boosts affect user behavior and whether they degrade or improve the user’s overall experience compared to “organic” results.
Pitfalls here include mixing artificially boosted items with truly high-rated items and losing a clear sense of whether the ranking system is performing well in an “unbiased” environment. It can also lead to confusion among stakeholders if the metric indicates lower precision but the boost was purposeful to meet a business goal (like promotion of new product lines).