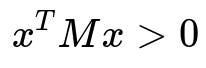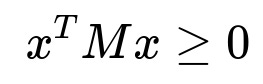ML Interview Q Series: How would you define positive-definite, negative-definite, positive-semidefinite, and negative-semidefinite matrices?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

A real square matrix M is typically discussed in the context of definiteness when M is symmetric. If M is complex, we often require M to be Hermitian. These conditions ensure that quantities of the form x^T M x (or x* M x in the complex Hermitian case) are real and thus can be consistently compared with 0.

Positive definite matrices

Here, x is any non-zero n-dimensional real vector (in the real case). The condition states that for every non-zero x, the scalar x^T M x is strictly greater than 0. Since M is assumed symmetric, this implies M has strictly positive eigenvalues. Positive definite matrices appear frequently in optimization and machine learning, especially in the form of Hessians or covariance matrices, since they ensure convexity or represent valid covariance structures.

Negative definite matrices

Again, x is any non-zero vector. This condition indicates all eigenvalues of M are strictly negative, and it often arises in settings involving concave functions. Matrices that are negative definite guarantee a strictly concave shape for the corresponding quadratic form.

Positive semidefinite matrices

For all x, the quadratic form x^T M x is non-negative. Such matrices may have zero eigenvalues as well as positive ones. In machine learning and statistics, positive semidefinite matrices are paramount because covariance matrices and Gram matrices (from kernel methods) must be positive semidefinite to preserve important properties like non-negativity of variances.

Negative semidefinite matrices

This condition states that for all x, x^T M x is non-positive. The matrix can have zero or negative eigenvalues. In certain optimization formulations, negative semidefinite matrices can appear when analyzing constraints related to concavity or in the design of second-order conditions for concave functions.

Symmetry (or Hermitian property in the complex case) is an important precondition for real (or complex Hermitian) matrices. Without that, the expressions x^T M x can take on complex or inconsistent values and definiteness properties become ill-defined or require additional considerations.

In machine learning, these concepts are closely related to optimization (e.g., checking if a Hessian is positive definite determines if we are at a local minimum). They also appear in kernel methods (where the kernel matrix must be positive semidefinite to define a valid inner product in feature space). In probabilistic modeling, covariance matrices must be positive semidefinite to ensure valid variances and correlations.

Checking positive definiteness in practice can be done via techniques like attempting a Cholesky decomposition. If the decomposition succeeds without numerical issues, the matrix is positive definite. For semidefiniteness, one can look at the eigenvalues and confirm all are non-negative for positive semidefiniteness or non-positive for negative semidefiniteness.

Below is a small Python snippet demonstrating how to check if a matrix is positive definite using NumPy:

import numpy as np

def is_positive_definite(M):
    try:
        # Attempt Cholesky decomposition
        np.linalg.cholesky(M)
        return True
    except np.linalg.LinAlgError:
        return False

# Example usage
matrix = np.array([
    [2, 1],
    [1, 2]
])
print(is_positive_definite(matrix))  # Expected True for this particular matrix

Why do we require symmetry or Hermitian property for definiteness?

Definiteness is tied to the quadratic form x^T M x. For real matrices, symmetry ensures x^T M x is always a real scalar. If the matrix were not symmetric, x^T M x could end up being non-real or not consistently represent a single scalar that can be compared with 0. In the complex case, Hermitian property (conjugate symmetry) similarly guarantees a real value for x* M x.

Why do positive (or negative) definite matrices matter in machine learning?

They arise in optimization—if the Hessian of a function is positive definite, that function is strictly convex, which guarantees a unique minimum. Positive semidefinite matrices are also crucial as kernel matrices in support vector machines and Gaussian processes, ensuring valid inner product interpretations. Covariance matrices in probabilistic models must be positive semidefinite to represent real-world variances and correlations.

How do we quickly test if a matrix is positive definite or semidefinite?

One common approach is checking if all eigenvalues of M are positive for positive definiteness, or non-negative for positive semidefiniteness. Numerically, attempting a Cholesky decomposition is a more efficient method in many cases. If the Cholesky factorization fails, that matrix is not positive definite. For semidefiniteness, a slightly different check involving eigenvalues or techniques such as checking principal minors can be used.

Can a matrix be indefinite?

Yes. If there exist vectors x that make x^T M x positive and others that make x^T M x negative, M is indefinite. An indefinite matrix can have both positive and negative eigenvalues. In optimization, an indefinite Hessian can indicate a saddle point of the function.