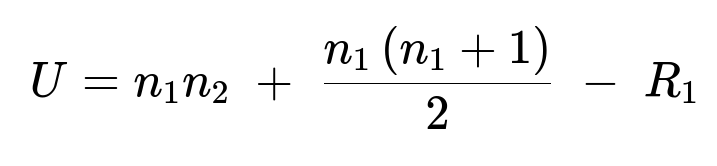ML Interview Q Series: How would you analyze a non-normal distribution in a small Uber Fleet A/B test and determine the winner?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Non-normal data can invalidate the assumptions of classical parametric methods such as the standard t-test. In smaller-scale scenarios like an Uber Fleet experiment, sample sizes might be limited and distributions might not adhere to normality. When facing non-normal distributions, non-parametric tests or resampling-based approaches are commonly employed to determine if one variation significantly outperforms another.
Why Non-Parametric Tests
Classical parametric tests (for instance, the two-sample t-test) assume data is drawn from a normally distributed population with similar variances. If that assumption breaks—especially with a small sample size—these methods become unreliable. Non-parametric tests such as the Mann-Whitney U test or the Wilcoxon signed-rank test do not assume normality, focusing instead on the ranks of the observed values.
Mann-Whitney U Test
A popular choice for comparing two independent samples (A and B) is the Mann-Whitney U test, also called the Wilcoxon rank-sum test in some contexts. In this method, you combine the data from both groups, rank all observations, and then sum the ranks of each group separately. The test statistic U for group 1 is computed using:
Here, n_1 is the number of observations in group 1, n_2 is the number of observations in group 2, and R_1 is the sum of ranks for group 1 (the sum of the rank positions for all data points belonging to group 1). Once U is obtained, it is usually compared to a distribution of U values under the null hypothesis of no difference between the groups. A p-value is calculated to reflect the probability that any observed difference in the ranks could be due to random chance.
Interpretation involves examining both the p-value and a measure of effect size. If p is below a chosen significance level (often 0.05), you conclude there is a statistically significant difference between the two variants. To measure which variant wins, you can look at median values or rank sums: if the median or average rank of group A exceeds that of group B in a meaningful way (and is statistically significant), A is considered better.
Bootstrap or Permutation Tests
When data is heavily skewed, extremely small, or has outliers, bootstrap or permutation methods can be more intuitive. You generate a large number of pseudo-samples from the observed data by sampling with replacement (in bootstrapping) or by reshuffling labels (in permutation tests). For each iteration, you compute a metric of interest (like mean difference, median difference, or another statistic) and build an empirical distribution of that metric. From this empirical distribution, you derive confidence intervals or p-values.
If the confidence interval of the difference in medians (or means, or other metrics) does not include 0 (or another baseline of no effect), you conclude the difference is significant. Comparing which variant has the higher (or lower, depending on the metric) average statistic tells you the winner.
Implementation Example in Python
Below is an example of how you might perform a Mann-Whitney U test in Python. This snippet illustrates two hypothetical groups, A and B, each representing a different variant.
import numpy as np
from scipy.stats import mannwhitneyu
# Hypothetical data
group_A = np.array([3.1, 2.4, 2.8, 3.7, 3.0])
group_B = np.array([2.5, 1.9, 2.2, 3.1, 2.7])
# Perform Mann-Whitney U test
stat, p_value = mannwhitneyu(group_A, group_B, alternative='two-sided')
print("Mann-Whitney U statistic:", stat)
print("p-value:", p_value)
# Simple decision
alpha = 0.05
if p_value < alpha:
print("Statistically significant difference. Check group medians to see which is better.")
else:
print("No significant difference detected.")
Depending on the sign of the difference between the central tendency of group_A and group_B (for example, median or mean rank), you can decide which variant is performing better.
How to Determine the Winning Variant
You evaluate the effect size and direction of the difference. If the median or mean rank of variant A is larger (for metrics where higher is better) and the p-value is below the significance threshold, you conclude that variant A wins. Otherwise, if variant B's distribution yields a higher median or average rank significantly, then B is the winner. In bootstrapping or permutation tests, one might compare the bootstrapped distributions of the metric between the two variants and see how often one variant surpasses the other in the chosen performance metric.
Potential Follow-Up Questions
How should you choose between Mann-Whitney U test and bootstrapping or permutation tests?
Non-parametric tests like the Mann-Whitney U test are straightforward and quick for smaller sample sizes. However, if the data distribution is extremely unusual (e.g., heavy tails, many zeros, or complex multi-modal shapes), bootstrapping or permutation tests can provide more robust and intuitive results since they do not rely on distribution assumptions. In practice, some prefer a permutation test for its conceptual clarity: it physically simulates the process of randomness in assigning data points to the two groups.
What if you have more than two variants to compare?
When comparing more than two groups in a non-parametric setting, the Kruskal-Wallis test is often used. This test generalizes the Mann-Whitney U approach to multiple samples. If the Kruskal-Wallis test indicates a significant result, you can apply pairwise non-parametric comparisons (Mann-Whitney U tests with an appropriate multiple-comparison correction) to identify which specific groups differ.
When can you approximate the Mann-Whitney U test to a normal distribution?
With sufficient sample size—commonly if both groups have more than 20 observations—some Mann-Whitney U test implementations use a normal approximation for computing the p-value. This is a convenient shortcut but is unnecessary if your software can handle the exact calculation directly, which is often feasible for smaller data sets.
What if the metric is ordinal or categorical rather than numeric?
Mann-Whitney U requires at least ordinal-level data, so if your metric is purely categorical with no inherent ranking, a chi-square test or Fisher’s exact test might be more appropriate. If the data has a meaningful order (for example, rating scales or ordinal feedback), the Mann-Whitney U test can still apply.
Is there a risk of misinterpreting the Mann-Whitney U test as a median test?
Yes. The Mann-Whitney U test compares distributions by examining the rank ordering of combined observations. It is often described as a test for median differences, but that is strictly correct only under certain conditions (e.g., similar shape distributions). The test is technically about the probability that a randomly selected value from group A will exceed a randomly selected value from group B. If shapes are very different, it might be more revealing to plot the distributions and not rely solely on a single median comparison.
Could outliers skew the decision?
Outliers can affect any statistical test, but non-parametric methods are generally more robust to extreme values than parametric ones. If outliers are present, it is still important to explore why they arose. Sometimes outliers represent genuine variations, and other times they may be data errors or noise needing special treatment. If legitimate, non-parametric tests or bootstrapping with robust statistics (like the median) can handle them better.
Could we perform transformations to approximate normality?
In some cases, applying transformations (for instance, logarithmic if the data is skewed to the right) may help the data approximate normality, enabling parametric tests. However, for an A/B test with limited data or uncertain distribution, it might be simpler and more transparent to apply a non-parametric or resampling approach that naturally handles unusual distributions.
Summary of Key Points
When the distribution is not normal—especially in low-data scenarios—non-parametric tests like the Mann-Whitney U or Wilcoxon rank-sum test can identify differences without relying on normality assumptions. Alternatively, bootstrap or permutation approaches generate empirical distributions of the metric differences. In both methods, you look for statistical significance (p-value or confidence interval) and then determine the winning variant by identifying which group has the superior metric outcome.
Below are additional follow-up questions
In a scenario where we have repeated measurements on the same subjects, can we still use the Mann-Whitney U test?
For repeated measurements or paired data, the Mann-Whitney U test is generally inappropriate because it does not account for the within-subject correlations. A suitable non-parametric alternative is the Wilcoxon signed-rank test if each subject experiences both conditions (like a paired design). If the data is heavily dependent across multiple time points or multiple treatments, more specialized methods (such as a non-parametric version of a repeated-measures ANOVA) may be required.
One subtle real-world concern is that your measurements could vary over time for reasons unrelated to the treatment, making a simple pairwise comparison misleading. For example, if data is measured weekly under different A/B conditions, external factors like seasonal patterns or changes in user behavior can confound results. Methods that explicitly model time effects or random effects (in a mixed model approach) can be more appropriate.
How do we handle situations where the metric of interest contains many zero values or is heavily zero-inflated?
When a significant proportion of data points are zero (or near zero), standard non-parametric rank tests can still be used, but your results might be less straightforward to interpret. A large cluster of zeros can mask or inflate treatment differences among non-zero values. You might consider:
Splitting the problem: first model the probability of a non-zero outcome (e.g., logistic regression or a Fisher’s exact test if it’s strictly 0 vs. non-zero), and second, given it’s non-zero, compare the values using a non-parametric test like Mann-Whitney.
Using specialized zero-inflated models if the metric is count-based (like zero-inflated Poisson or negative binomial approaches).
A potential pitfall is failing to recognize that the zero values may come from a process different from the continuous portion of the distribution. For instance, if many customers don’t use a certain feature at all (zero usage), while others use it multiple times, mixing them under a single test can obscure meaningful outcomes.
If we have limited sample sizes and the difference fails to reach statistical significance, how do we interpret the practical significance?
Limited sample size can reduce statistical power, making it harder to detect differences even if they exist. If you find a difference in medians (or means) that is relevant from a practical or business standpoint but not statistically significant given your sample, it may be premature to conclude “no effect.” Instead, consider the following:
Look at confidence intervals or credible intervals (in a Bayesian setting) for your effect size to gauge the plausible range of the difference.
Evaluate practical or business-oriented significance: for example, in a real application, a 2% improvement could be huge even if p > 0.05.
Collect more data, if possible, to increase the power of the test.
Use power analysis or Bayesian approaches that allow you to incorporate prior beliefs or a cost-benefit framework.
A common pitfall here is simply discarding the result and concluding that there is “no effect.” Sometimes the test is simply underpowered.
How do we address the issue of multiple comparisons if we run numerous non-parametric tests simultaneously?
In real-world experiments, you might compare multiple metrics or multiple segments of users. Each additional test inflates the chance of a false positive. You would typically adjust your significance threshold using methods such as Bonferroni correction (dividing alpha by the number of tests) or the more powerful Holm-Bonferroni procedure.
However, these corrections can be conservative, especially with small samples, and may increase the risk of Type II errors (failing to detect real differences). A nuanced approach might be:
Pre-register which hypothesis or metrics are primary and which are secondary.
Apply correction only to secondary or exploratory metrics while focusing on primary outcomes with the standard alpha level.
Failing to do so can cause confusion when multiple metrics show borderline significance, leading to questionable claims of success.
What if our distribution is multimodal or made up of distinct subpopulations?
Sometimes you’ll discover that your data has multiple peaks. For instance, in an A/B test for a feature used by two very different sets of users, you could have a bimodal or multimodal distribution. Non-parametric tests still work in principle, but interpreting the results might become complex because one variant might be better for one subset while the other variant is better for another.
A possible pitfall is overlooking the fact that aggregated results mask subgroup differences. The next step might be a segmentation analysis: break down the data by meaningful user segments and run separate tests, or use a clustering technique to isolate different modes in the distribution. This can reveal patterns like “Variant A is superior for advanced users but not for novices,” which a single aggregate test might conceal.
How could a Bayesian approach help when dealing with small sample sizes and non-normality?
A Bayesian method, such as a Bayesian AB test using Markov Chain Monte Carlo (MCMC), can be more flexible with unusual distributions and small data sets. Instead of p-values, you obtain a posterior distribution over the metric’s difference. You can then compute the probability that one variant exceeds another by at least a certain threshold. This method naturally incorporates prior knowledge about typical effect sizes or distribution shapes if such information is available.
The pitfall is that Bayesian approaches require careful selection of priors, which can introduce subjectivity. An improperly chosen prior might bias the conclusions, especially with small sample sizes. Nonetheless, for certain real-world cases, the interpretability and flexibility of a Bayesian framework can be highly valuable.
What are the trade-offs between using a parametric approach on transformed data versus using a non-parametric test?
When faced with non-normal data, one option is to transform the data (e.g., using a log transform if the data is right-skewed) so that a parametric test’s assumptions become more reasonable. Another option is to apply a non-parametric test directly. Each approach has trade-offs:
Transforming data can simplify the interpretation if the transformed metric still has a meaningful interpretation. However, in some cases, a log transform might distort the meaning of differences (e.g., differences in log scale are multiplicative in the original scale).
Non-parametric tests require fewer assumptions but may have slightly less power if the data could have been made approximately normal through an appropriate transformation.
A subtlety arises when transformations fail to normalize the distribution: you could inadvertently misapply a parametric test. Checking diagnostic plots (e.g., Q-Q plots) or performing goodness-of-fit tests can guide whether a transformation is actually improving normality.