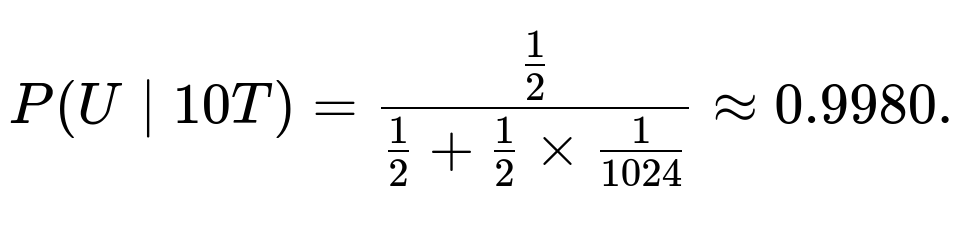ML Interview Q Series: Identifying an Unfair Coin After Five Tails Using Bayesian Inference
Browse all the Probability Interview Questions here.
1. There is a fair coin (one side heads, one side tails) and an unfair coin (both sides tails). You pick one at random, flip it 5 times, and observe that it comes up as tails all five times. What is the chance that you are flipping the unfair coin?
This problem was asked by Facebook.
Think about the underlying scenario from a Bayesian perspective. We have two coins:
• A fair coin (probability of heads = 1/2, tails = 1/2). • An unfair coin that is double-tailed (probability of tails = 1, heads = 0).
We randomly pick one coin, so initially each coin has a prior probability of 1/2. We then flip the chosen coin 5 times and observe 5 consecutive tails (denote this event as 5T). We want to find the posterior probability that the chosen coin is the unfair (double-tailed) coin given we observed 5 tails in a row.
In Bayesian terms, we write:
• Let F = event “we picked the fair coin.” • Let U = event “we picked the unfair coin.” • We want to compute the posterior probability
The prior probabilities are:
Now, we look at the likelihood of observing 5T from each coin:
• From the fair coin, the probability of getting 5 consecutive tails is
• From the unfair (double-tailed) coin, the probability of getting 5 consecutive tails is 1 (since every flip will be tails).
Using Bayes’ rule,
Substituting the relevant numbers:
Hence:
So the probability is
In other words, there is a 96.97% chance that you are flipping the unfair coin after observing 5 tails in a row.
Below is a simple Python snippet illustrating the same calculation:
import math
# Prior probability for each coin
p_fair = 0.5
p_unfair = 0.5
# Likelihoods
likelihood_fair_5T = (0.5**5) # (1/2)^5
likelihood_unfair_5T = 1.0 # Always tails
# Posterior using Bayes
numerator = likelihood_unfair_5T * p_unfair
denominator = (likelihood_unfair_5T * p_unfair) + (likelihood_fair_5T * p_fair)
posterior_unfair_5T = numerator / denominator
print(posterior_unfair_5T) # 0.9696969696969697
This confirms that the posterior probability is 32/33.
Below are several potential follow-up questions that often arise in rigorous machine learning or technical interview settings. Each is answered in detail to ensure full clarity on the concepts and reasoning involved.
What if there were more flips, or a different number of tails?
If we flipped the chosen coin (n) times and observed (k) tails, you would compute:
• Probability of observing (k) tails from the fair coin is ((\tfrac12)^k \times (\tfrac12)^{n-k}) = ((\tfrac12)^n). • Probability of observing (k) tails from the unfair coin is 1 if (k=n) (all tails), otherwise 0 if even a single head is seen.
In the exact scenario of “all (n) flips are tails,” the Bayesian update becomes:
$$P(U \mid \text{all } n \text{ tails})
= \frac{1 \cdot \tfrac12}{1 \cdot \tfrac12 + \bigl(\tfrac12^n\bigr) \cdot \tfrac12} = \frac{\tfrac12}{\tfrac12 + \tfrac{1}{2},\tfrac{1}{2^n}} = \frac{\tfrac12}{\tfrac12 + \tfrac{1}{2^{n+1}}}.$$
When (n) is large, (\tfrac{1}{2^n}) becomes extremely small, so the posterior probability that the coin is unfair gets closer and closer to 1. In practice, just a few consecutive tails can make it very likely that you have the unfair coin.
On the other hand, if you observed (k) tails out of (n) flips, but not all tails, the probability of that outcome from the unfair coin would be 0. That would immediately update your posterior probability to 0 that you have the double-tailed coin (unless you consider some other prior or possibility of partial bias, but in the strict sense of a double-tailed coin, any single head observation rules it out entirely).
How does this problem relate to Bayesian statistics?
The problem is a textbook example of Bayesian inference. You have:
• A discrete set of hypotheses (fair coin vs. unfair coin). • A prior distribution over those hypotheses (each coin initially has probability 1/2). • Observed data (in this case, the outcome of flips). • A likelihood function describing how probable the data is under each hypothesis.
Using Bayes’ theorem, you update your belief (the posterior) based on how consistent the observed data is with each hypothesis. As soon as you observe multiple tails in a row, the hypothesis of “unfair coin” becomes increasingly probable, because it explains these data (all tails) with much higher likelihood.
Could this be done using a Beta distribution approach?
If you have a coin with an unknown bias (p) for tails, a common Bayesian approach is to place a (\mathrm{Beta}(\alpha,\beta)) prior on (p). After observing data, you would update the posterior to (\mathrm{Beta}(\alpha + \text{number of tails}, \beta + \text{number of heads})). However, in this question, the “unfair coin” has (p=1) for tails, so it is a separate discrete hypothesis altogether (not just a continuous range of possible biases). You essentially have a mixture model:
• Hypothesis 1: (p=\tfrac12) • Hypothesis 2: (p=1.0)
So you do not need a continuous Beta approach unless you wanted to generalize the problem to coins that can have any bias (p). Then you might incorporate an extra “point mass” at (p=1) or treat it as a separate hypothesis in a hierarchical model. In short, for a coin that is definitely double-tailed vs. one that is definitely fair, straightforward application of Bayes’ rule with discrete hypotheses is enough.
In practice, how many tails in a row would I need to be practically certain I have the unfair coin?
From the formula:
as (n) grows, (\tfrac1{2^n}) becomes so small that the posterior gets extremely close to 1. For example:
• For (n=5), we get 32/33 ≈ 0.9697. • For (n=10), the probability that the fair coin shows 10 tails in a row is (\tfrac1{2^{10}}=\tfrac1{1024}), so
• For (n=20), (\tfrac1{2^{20}}=\tfrac1{1{,}048{,}576}). The posterior that you have the unfair coin becomes incredibly close to 1.
Is there a scenario where observing 5 tails could mislead me if the coin was actually the fair one?
It’s still possible that you picked the fair coin and happened to observe 5 tails in a row. That event has probability (1/32). But compared to the probability of observing 5 tails in a row from the unfair coin (which is 1), the data strongly favors the unfair coin. Bayesian methods do not say it is impossible for the fair coin to produce 5 tails in a row; they simply give you a posterior probability that quantifies how much more likely one hypothesis is relative to the other. With 5 tails, the posterior heavily favors “unfair,” but it is not 100% until you see a huge number of tails in a row (or confirm in some other way).
How does a manufacturing defect or real-world imperfection change this analysis?
Real coins may deviate slightly from 50-50. Suppose a real “fair” coin might be 49.9% to 50.1% for heads vs. tails. Or a “double-tailed” coin might still have a tiny chance of flipping incorrectly (like if physically damaged). In real-world scenarios, you could model these small deviations by placing a prior distribution over the coin’s bias (p). The essence of the Bayesian update remains the same: the hypothesis that best explains the data (based on the likelihood) will dominate after multiple observations, as long as you keep your model assumptions consistent with physical reality.
Could we incorporate a different prior if we had prior knowledge?
Yes. If you believed, for example, that it is more likely that you are handed a normal coin than a trick coin, you might set (P(F)) to 0.9 and (P(U)) to 0.1. Then the posterior probability with 5 tails in a row would be:
You can generalize the formula accordingly. The main idea is that if your prior strongly favors one hypothesis, you need more data to overcome that prior. Conversely, if your prior strongly favors the other hypothesis, you might quickly conclude it is correct upon seeing only a little evidence.
Example of how you might code a quick Bayesian inference for multiple flips and flexible priors
def posterior_unfair(n_tails_observed, total_flips, p_unfair_prior, p_fair_prior):
"""
Returns the posterior probability that the coin is the unfair (double-tailed) coin.
:param n_tails_observed: number of tails observed
:param total_flips: total number of flips
:param p_unfair_prior: prior probability of picking the unfair coin
:param p_fair_prior: prior probability of picking the fair coin
"""
# Probability that fair coin yields the observed outcome (all tails, if n_tails_observed == total_flips)
if n_tails_observed == total_flips:
# Probability of all tails with a fair coin
likelihood_fair = (0.5 ** total_flips)
else:
# If not all tails, the double-tailed coin cannot produce such data
# For partial tails we only do this if we define some model for partial bias,
# but strictly for "double-tailed or fair", the unfair coin has 0 chance if any head appears.
likelihood_fair = (0.5 ** n_tails_observed) * (0.5 ** (total_flips - n_tails_observed))
# Probability that the unfair coin yields the observed outcome
if n_tails_observed == total_flips:
likelihood_unfair = 1.0
else:
likelihood_unfair = 0.0
# Apply Bayes rule
numerator = likelihood_unfair * p_unfair_prior
denominator = numerator + (likelihood_fair * p_fair_prior)
return numerator / denominator if denominator != 0 else 0.0
# Example usage:
print(posterior_unfair(5, 5, 0.5, 0.5)) # 5 tails out of 5 flips, prior 0.5 vs 0.5
This snippet extends naturally if you wanted to handle different priors. You could also modify the likelihood computation if you wanted a continuous range of biases instead of a single fair coin vs. a single unfair coin.
Summary of key insights
• The posterior probability that you have the unfair coin, after observing 5 tails in a row with equal priors, is (32/33), which is approximately 96.97%. • Bayesian thinking clarifies how to incorporate priors and update those beliefs as soon as new data (flips) become available. • Even with small sample sizes, the difference in likelihood between a fair coin and a double-tailed coin is drastic if you see multiple consecutive tails. • In real-life scenarios, you might incorporate a small chance that the coin is biased in other ways or not truly double-tailed, but the overall Bayesian approach remains.
Additional follow-up questions to probe deeper understanding
What if you see one head after several tails? That instantly reduces the likelihood of the double-tailed coin to zero under the strict model that the unfair coin has no heads. Therefore, you would conclude with probability 1 that you have the fair coin if you strictly maintain the “double-tailed vs. fair coin” assumption.
Why is Bayes’ theorem important in machine learning contexts? Machine learning often involves updating beliefs about models or parameters based on evidence. Bayesian methods offer a principled approach to do that, handle uncertainty, and combine prior knowledge with observed data. This problem is a simplified example of that reasoning pattern.
How might an interviewer test if you really understand the calculation? They might ask for intermediate steps of Bayes’ rule, or how the formula changes with 4 tails vs. 5 tails, or what if there’s a known bias of 0.75 for tails in the “fair” coin, or what if you have a prior of 1% for the trick coin. Thorough understanding of each piece (prior, likelihood, posterior) is key.
Below are additional follow-up questions
What if the experiment is performed over multiple sessions, possibly switching the coin in between?
Imagine you conduct the flipping in two or more distinct sessions. Between these sessions, there is a possibility that the coin you were flipping might have been switched with another randomly selected coin from the same original pool (one fair coin, one double-tailed coin). This complicates the analysis because, after the first session, you do not necessarily continue with the same coin into the second session.
To address this, you must keep track of the probability that you had the unfair coin at the end of each session, and then account for the probability that you switch coins. The approach would be:
You complete the first series of flips and compute your posterior that you have the unfair coin using the Bayesian update. Then, if there is a chance the coin is swapped, you consider the transition probabilities that you either keep your current coin (with the posterior probability that it’s unfair or fair) or exchange it for the other coin. This creates what amounts to a Markov chain, where the state is “currently holding the unfair coin” or “currently holding the fair coin,” and you incorporate the data you gather in the next session to update those probabilities all over again.
A potential pitfall is failing to recognize that the coin might change between sessions and automatically applying the posterior from the first session to the second session’s flips. The correct approach is to combine the posterior after session one with the switching probability, which leads to a new prior for session two, and then you update again based on session two data. Real-world issues might arise when the switching probability is unknown, requiring assumptions or additional data about how often coins get swapped.
How would the result change if the coin flips are not i.i.d.?
The original problem implicitly assumes each coin flip is an independent and identically distributed event. In some physical situations, flips may not be perfectly independent—for example, if you spin the coin in a highly consistent way or if the coin has a known mechanical bias that changes with repeated use. If flips are not independent, the probability of observing consecutive tails under the “fair coin” hypothesis could differ from the simple ((\tfrac12)^5) model.
To handle this, you would need a model for the correlation structure among flips. For instance, you might have a Markov model where each flip depends on the previous outcome. This alters the likelihood of observing a particular sequence of flips. You then plug that modified likelihood into the Bayesian update. A major pitfall here is using the simple ((\tfrac12)^5) when flips are correlated; that can lead to incorrect posterior inferences. Real-world examples might include certain spinning machines or coin-tossing robots that nearly replicate each toss in a systematic way, deviating from the ideal 50-50 assumption. Always confirm the i.i.d. assumption if possible.
How does this logic extend to a scenario with three coins: one fair, one double-tailed, and one double-headed?
You can expand the same Bayesian approach to handle multiple hypotheses. Suppose you have three coins:
One fair coin with probability 1/2 for tails, One double-tailed coin with probability 1 for tails, One double-headed coin with probability 0 for tails.
If you pick one randomly at the start, each coin has a prior probability 1/3. Observing 5 consecutive tails rules out the double-headed coin (which would not produce any tails) entirely. Thus, the posterior probability for the double-headed coin after observing 5 tails is zero under this strict interpretation. Meanwhile, you compare the likelihood of the fair coin producing 5 tails, which is ((1/2)^5), against the likelihood of the double-tailed coin producing 5 tails (which is 1). The Bayesian update for these two remaining coins becomes the same as in the original problem, but now with different priors. Specifically, after ruling out the double-headed coin, the sum of the posterior probabilities for the fair and double-tailed must be 1, but you start from each having 1/3 prior, then normalize to account for the eliminated coin. A subtle point here is that you must assign zero posterior to the coin that cannot possibly produce the observed data and re-normalize among the remaining ones.
Can we approach this question from a frequentist hypothesis testing perspective instead?
Yes, you can attempt to frame the problem as a hypothesis test where the null hypothesis might be “the coin is fair” and the alternative hypothesis is “the coin is double-tailed.” If you assume a test at a certain significance level, you might consider the event of seeing 5 tails in a row to be extremely unlikely under the fair-coin hypothesis with probability ((\tfrac12)^5 = \tfrac{1}{32}). You could then compute a p-value (which, in this scenario, is exactly 1/32 for seeing at least 5 tails in 5 flips if your test is that extreme). If that p-value is below your significance threshold, you reject the hypothesis that the coin is fair. However, the frequentist approach does not immediately give you the probability that the coin is double-tailed. It only tells you whether the fair-coin assumption is inconsistent with the data under a chosen threshold. The Bayesian method directly gives you the posterior probability that it is double-tailed. The pitfall here is that you cannot interpret the p-value itself as the probability that you have the fair coin. They are conceptually different: a frequentist test does not attach probabilities to hypotheses in the same way Bayesian inference does.
What if we incorporate a cost function where being wrong about the type of coin has serious consequences?
In certain real-world problems, you might care about the cost of a wrong decision. For instance, if incorrectly labeling the coin as unfair is harmless, but incorrectly labeling it as fair has a huge risk, your optimal decision might differ from a simple posterior-threshold rule. You could adopt a Bayesian decision-theoretic approach, assigning a cost to each type of error: picking the fair coin when it’s actually unfair, or picking the unfair coin when it’s actually fair. After computing the posterior probabilities, you choose the action (deciding the coin’s identity) that minimizes expected cost.
A subtlety is that even if the posterior probability that the coin is unfair is, say, 80%, you might still label it “unfair” if the cost of missing the unfair coin is extremely high compared to the cost of a false alarm. Another subtlety arises if there is a third decision option (e.g., “collect more data” by flipping more times) with an associated cost. Then you are doing a full Bayesian decision analysis, factoring in the benefit of gaining more information versus the cost or time of additional flips.
What happens if you see a coin land on its edge?
Sometimes, a real coin might land and stay balanced on its edge. This introduces an outcome outside the standard heads-or-tails scenario. In the most purist sense, the original problem does not consider this possibility. If we integrate that new outcome into the model, we need an additional parameter: the probability of landing on edge for each coin. Under a double-tailed coin, you might argue that the chance of landing heads is zero but the chance of landing edge is possibly the same or different as for a fair coin. As soon as you expand the outcome space, you must recalculate the likelihood functions to reflect the new third outcome. This can significantly affect the posterior if the probability of landing on edge is not negligible. A major pitfall is ignoring these rare events and inadvertently skewing your probability calculations. In most standard interview contexts, we assume that the probability of landing on edge is so negligible that the two-outcome model remains valid, but a real-world gambler or an advanced interviewer might explore this corner case.
How would you adjust the posterior if the coin was observed to spin in the air and then not complete the final landing?
Sometimes you might observe partial flips or a scenario where the coin is caught mid-air. This can complicate the data you collect. If a flip was incomplete, you might discount that flip entirely or treat it as missing data in a Bayesian framework. With missing data, you either ignore that flip in the likelihood calculation or you model the probability that you might see partial results. If the partial flip itself reveals some bias (for instance, you glimpse the face of the coin in mid-air), you might incorporate partial information. The key is to define a proper likelihood function that matches the evidence you have. A subtle pitfall arises if you just ignore partial flips without adjusting your model, which can bias your results if certain partial flips are more likely to reveal tails or heads. In a rigorous Bayesian approach, you would incorporate a probability distribution over what partial observation you made and how that might update your belief about the coin.
What if there's a physical chance that the double-tailed coin is actually chipped or can produce a head in rare cases?
In reality, a “double-tailed coin” might not produce a head exactly 0% of the time. Perhaps there is a tiny manufacturing defect or an external factor that can somehow cause a flipside appearance. If you wanted to be extremely precise, you might introduce a small parameter (\epsilon) for the double-tailed coin, representing the slim probability of seeing a head in an extreme edge case. The likelihood for observing a certain number of heads or tails from that coin would then be ((1 - \epsilon)^\text{(tails)} \times \epsilon^\text{(heads)}). You would no longer be able to rule out the double-tailed coin the moment you see a single head. Instead, it would become less likely but not impossible. This is especially relevant in real production lines or trick coins that are not ideal. The pitfall is labeling it as definitely not the double-tailed coin as soon as one head is observed. If you do that prematurely but, in reality, (\epsilon\neq 0), you will underestimate your uncertainty. Properly modeling (\epsilon) and updating the posterior with a near-zero but non-zero chance of heads yields a more realistic but more complex analysis.
What if we suspect the experimenter might have a bias when flipping the coin?
Suppose the person tossing the coin is not flipping it randomly but performing a biased technique that increases the chance of tails. This scenario means that even the “fair coin” might show more tails than expected by an ideal 50-50 model. You would then have to model the effect of the flipper’s bias. For example, if the flipper’s technique yields tails with probability (p\neq 0.5) for the fair coin. In that case, you would replace ((\tfrac12)^5) with (p^5) for the chance of seeing 5 tails. The unfair coin might remain close to probability 1 of tails per flip, but if it is also impacted by the flipper’s method, maybe it’s still close to 1, or exactly 1, or some other number. As soon as you define these revised likelihoods, you can apply the same Bayesian formula. A subtlety is that we rarely know the precise flipping bias, so you might place a prior distribution on the flipper’s bias and try to integrate over that. The pitfall here is ignoring the human factor and incorrectly concluding the coin is extremely likely to be the double-tailed one when in fact it was just a strongly biased flipping technique on a fair coin.
How would we handle sequential decision-making, for example stopping early if the evidence is strong enough?
In many practical experiments, you do not decide in advance to flip exactly 5 times. You might adopt a sequential testing procedure. You flip the coin once, see the result, then decide whether to flip again or stop. In Bayesian terms, after each flip, you update your posterior probability that the coin is unfair, and you have a strategy that decides whether more data is needed. This leads you into Bayesian sequential decision-making or sequential hypothesis testing. You might fix a threshold such that if (P(\text{unfair} \mid \text{data so far})) exceeds some value, you conclude “unfair coin” and stop flipping, or vice versa. One subtlety is that repeated significance testing can inflate false positives if you approach it incorrectly from a frequentist standpoint. A Bayesian solution is more coherent because you can keep updating the posterior in real time. The pitfall is to keep flipping until you see a suspicious run of tails, then call it unfair, ignoring that your procedure was adaptively choosing to continue flipping. Proper sequential analysis accounts for the changing probability distribution and the fact that you might have tried multiple times.
Can we interpret the posterior odds form of the calculation to gain extra insight?
You could recast the Bayesian update in terms of odds. The posterior odds of unfair vs. fair equals the prior odds times the Bayes factor. The prior odds here start at 1:1 because each coin has probability 1/2. The Bayes factor is the ratio of the probabilities of the observed data under the two hypotheses. In the case of 5 tails in a row, that ratio is (1 ,/, (\tfrac12)^5 = 32). Thus, the posterior odds are (1 \times 32 = 32). This means the “unfair” hypothesis is 32 times as likely as the “fair” hypothesis, so the posterior probability is (32/(32+1)=32/33). A key benefit of odds form is that it can be easier to update repeatedly, especially if you keep seeing more tails. You simply multiply the current odds by the Bayes factor for the new data point. The pitfall is forgetting to convert from odds to probability correctly or ignoring the possibility that new data might have a different Bayes factor if you see a head.
How might real-world coin trickery go beyond simply having both sides the same?
A cunning trick coin might not just be double-tailed. It might be weighted or milled in a way that manipulates its flipping physics. Such a coin can produce near 100% tails but not strictly 100%. Or it might appear fair but have some concealed mechanism. In a professional or magic setting, the difference can matter: is it truly impossible to flip heads, or is it just extremely unlikely? If you wanted to be robust to various forms of trickery, you might model the trick coin with an unknown distribution for heads vs. tails, placing a prior heavily biased near 1 for tails. As you gather data, you update that distribution. The pitfall is assuming that the trick coin can never produce heads and concluding you are certain it is fair upon seeing a single head, when a real trick coin might have an extremely low but not zero chance of heads. Only a thoroughly tested model for the coin’s behavior avoids such misclassification.
How does this analysis change if we cannot trust the reported outcomes?
An unusual but important real-world twist is if someone else is reporting the coin flips, and we suspect potential dishonesty or observational error. Then the event “5 reported tails” might not perfectly match “5 actual tails.” You need to account for the possibility that the observer is lying or that errors creep into the reported data. That means you define a separate likelihood function for the probability of reported outcomes given the true outcomes. For instance, the likelihood of seeing a “fake head” in the observer’s notes might be some small probability if the observer randomly misrecords results. A major pitfall is uncritically trusting the reported results. If you do not incorporate the possibility of false reporting, you might drastically over- or underestimate your posterior probabilities. This scenario extends beyond coin flips to many data-collection processes in machine learning, where label noise can distort conclusions if not modeled properly.
What if the fair coin is also slightly bent or has a small chance of landing heads on one side and tails on the other side?
Imagine the fair coin is not a perfect 50-50 coin but something like 49% heads, 51% tails. The so-called “unfair coin” might still be double-tailed, or it might also have a slight chance for heads if physically defective. For a more generalized setting, you label the coins with different probabilities of tails, say the fair coin has probability (p_f\approx0.5) for tails, and the trick coin has probability (p_u\approx1). You then compute the likelihood of 5 tails as (p_f^5) vs. (p_u^5). If (p_u) is truly 1, the likelihood ratio is (p_u^5 / p_f^5 = 1 / p_f^5). If (p_u) is close to 1 but not exactly 1, then it is something like ((0.999)^5 / (0.51)^5). This shows that even a tiny difference from 1 can reduce the likelihood ratio compared to the ideal double-tailed scenario. The analysis is straightforward: you do the Bayesian update with these new likelihoods. The main pitfall is assuming exact values for these probabilities without measuring them, or ignoring that physical coins seldom match neat theoretical probabilities.
What if we only observe partial outcomes or subsets of flips due to data corruption?
In data-driven fields, it is possible that one or more of the 5 flips is not recorded properly, giving us incomplete data. We might know that 3 flips were tails, but for 2 flips, the record is missing. If you define the probability that missing data flips were tails or heads, you can incorporate that into your likelihood. You sum or integrate over all possible ways those missing outcomes might have occurred. If you have no clue, you assign a prior of 50-50 for each missing flip under the fair coin and 100% tails under the double-tailed coin. This means the likelihood of the partial outcome from the fair coin is ((\tfrac12)^3 \times ( \tfrac12 )^{(\text{missing flips})}) integrated in a certain way, while from the double-tailed coin it remains 1 for any tails that were observed. The pitfall is ignoring missing data or incorrectly treating it as heads or tails with certainty, which can severely skew your posterior estimates.
How does this problem illustrate the use of likelihood versus probability of a hypothesis?
Often, learners confuse the probability of observing the data given a hypothesis (the likelihood) with the probability of a hypothesis given the observed data (the posterior). This classic coin-flip problem helps clarify that the probability of 5 tails given the unfair-coin hypothesis is 1, whereas the probability of 5 tails given the fair-coin hypothesis is ((\tfrac12)^5). To find the posterior probability of the coin being unfair, we need to multiply those likelihoods by the prior probabilities and normalize. A subtle pitfall is forgetting the normalization step (summing over all hypotheses). Another pitfall is interpreting the likelihood as the posterior probability. Carefully distinguishing the two is central to Bayesian statistics, and the coin-flip scenario is an excellent demonstration of how they fit together.
How would the answer differ if our prior belief strongly favored the fair coin?
If you start with an extreme prior, say 0.99 probability for the fair coin and only 0.01 for the double-tailed coin, then after seeing 5 tails, the posterior probability of having the unfair coin changes significantly, but it may not reach as high as in the case of 0.5 prior. The posterior is computed by:
This value might still be quite large if ((1/2)^5) is small enough, but not as large as 32/33. This reveals that strong priors can dominate unless the observed data are overwhelmingly unlikely under the favored hypothesis. The subtlety is that if your prior belief is anchored to the notion that double-tailed coins are extremely rare, it may take more flips to overcome that prior. This underscores how Bayesian inference merges both prior belief and evidence. A real-world pitfall is ignoring the possibility that your prior might be incorrect. Overly confident priors can slow learning from data or lead to erroneous conclusions if those priors are off-base.
How does this example connect to real-world A/B testing in large tech companies?
At a large technology company, A/B tests often compare a “standard” experience (fair coin) to a “treatment” experience that might yield very different user metrics (like a double-tailed coin). Observing extreme outcomes in your test group might push your Bayesian or frequentist analysis to conclude that the new feature is drastically different from the baseline. Much like flipping tails repeatedly, you see a large or small metric that is unlikely under the status quo. Then you update your beliefs about whether your new feature is indeed better or fundamentally different. However, in real experiments, “double-tailed” might equate to an extremely large effect size. One subtlety is that user behaviors can vary over time, so you need robust confidence intervals or posterior distributions. A pitfall is ignoring the possibility that the test environment might bias the results in the short term, much like a biased coin flipper.
How does the law of large numbers and the idea of repeated sampling apply here?
If you keep flipping the coin many times, the empirical frequency of tails will converge to the true underlying probability of tails in the long run, provided flips are i.i.d. If it truly is a double-tailed coin, eventually you will almost surely see tails on every flip, and your posterior that it is unfair will approach 1. If it is fair, about half the flips should be tails in the long run. In practice, for only 5 flips, you do not have a large sample, but the difference between seeing all tails versus expecting about half heads is stark enough that the posterior heavily leans toward the unfair coin. The pitfall is concluding something too quickly if the difference in outcomes is not so extreme or if you do not track enough flips. But because the difference between 50% tails and 100% tails is so large, even a short run of consecutive tails can cause a strong belief that the coin is double-tailed.
How can we generalize this problem to a setting where the coin might have various biases in a continuous range?
You could imagine a family of hypotheses labeled by a parameter (p) for the probability of tails. One extreme is (p=0.5) (fair coin), another extreme is (p=1) (double-tailed). In a full Bayesian approach, you place a prior distribution over (p), such as a Beta distribution. Observing 5 tails updates that distribution to shift its mass toward larger (p) values. If you specifically allow for the possibility that (p=1) with some discrete probability mass, then your posterior might place some probability on that exact point while also distributing some probability across values near 1. The mathematics then reflect a mixture of a Beta posterior with a point mass at 1. The subtlety is how you partition your prior between the continuous range of (p \in [0,1]) and the point mass at (p=1). This approach is more flexible if you suspect the coin might be nearly double-tailed but not precisely 100%. A major pitfall is inadvertently zeroing out the possibility of (p=1) if your prior does not allow it or forgetting to handle it as a special case.
How might you confirm your Bayesian calculation in a simulation?
A straightforward verification is to run a Monte Carlo simulation. You simulate many trials of picking a coin at random, flipping it 5 times, and counting how often you see 5 tails in a row. You then observe among those 5-in-a-row outcomes, how often they came from the double-tailed coin. That frequency across many trials should match the posterior probability given by the analytical Bayes solution, around 32/33. A subtlety is ensuring your simulation is coded correctly: you must randomly pick a coin, flip it 5 times according to that coin’s bias, and then record only those runs that yielded 5 tails, measuring the fraction that were from the unfair coin. The pitfall is to measure the fraction incorrectly, for example by measuring the fraction of all coin picks from the unfair coin that yield 5 tails, which is not the same as the fraction among all 5-tail outcomes. This is a classic case of carefully conditioning on the observed event.
How might the result differ if you keep flipping until you see 5 tails in a row?
A nuanced question arises if the experiment is “we flip the coin until we get 5 tails in a row,” and then ask the probability that the coin is unfair. This is different from flipping exactly 5 times. The distribution of how many flips it takes to first see 5 consecutive tails is quite different under a fair coin than under a double-tailed coin. The likelihood function is the probability of first achieving 5 consecutive tails on a certain flip count. Under a fair coin, that probability is determined by analyzing patterns of heads and tails. Under a double-tailed coin, you will always get 5 tails in a row starting from the first 5 flips. Because you keep flipping until that event occurs, you must set up the Bayesian update accordingly, using the distribution for the “first time 5 consecutive tails occurs.” The pitfall is using the simple ((\tfrac12)^5) for this scenario, which does not account for the waiting time aspect. Correctly modeling the experiment design is essential to get the right posterior.
How would partial or ambiguous flips be handled if, for example, the coin hits an obstacle mid-air and one flip is not clearly heads or tails?
In some physical settings, one of the flips might be invalid if the coin hits an obstacle or is snatched out of the air before fully landing. If you see 4 valid tails and 1 ambiguous or incomplete result, do you count that as 5 tails, 4 tails, or do you discard the entire sequence and start over? Depending on your approach, you could treat the ambiguous flip as missing data (and attempt a partial-likelihood approach) or define the rule that an incomplete flip is discarded from the sequence count. This matters because it changes your data and thus your posterior. A major pitfall is to treat ambiguous flips as tails by default, artificially inflating the count of tails. Another pitfall is to ignore ambiguous flips altogether even though the partial outcome might contain information. A rigorous approach is to define a likelihood for each possible outcome of an ambiguous flip if you had partial knowledge, though that often complicates the analysis considerably.
How can we extend this reasoning to classification problems in machine learning?
In classification tasks, you often have two competing models (akin to two coins) that you suspect might generate your data. Observing a set of labeled examples is like seeing a series of heads or tails. You compute the likelihood of that dataset under each model and use Bayes’ rule to update your belief. Much like concluding the coin is unfair after enough tails, you might conclude one model is more plausible if the observed data have a much higher likelihood under that model. For instance, in a spam detection scenario, model A might assume certain word distributions, while model B might assume others. Observing a suspicious concentration of certain words might drastically favor model B (unfair coin). The pitfall is ignoring prior information, such as the prevalence of spam vs. not-spam, leading to suboptimal classification decisions. The Bayesian approach can handle that elegantly by adjusting the posterior based on priors and the likelihood ratio of the observed data.
How might you re-check your arithmetic in the heat of an interview?
In a stressful interview setting, a common pitfall is to mix up the roles of prior, likelihood, and posterior. A recommended check is to rewrite Bayes’ rule: posterior = (likelihood × prior) / evidence. Identify each quantity carefully:
The prior for each coin is 1/2. The likelihood of 5 tails is 1 for the double-tailed coin, ((1/2)^5) for the fair coin. The evidence is the sum of each hypothesis’s prior multiplied by its likelihood.
You should confirm the final fraction. If you do it all carefully, you arrive at 32/33. A red flag is if you get a fraction that’s obviously bigger than 1 or smaller than 0. Another quick check is the posterior odds form: posterior odds = prior odds × Bayes factor. Prior odds here are 1:1, Bayes factor is 1 / ((1/2)^5 = 32). Thus, posterior odds are 32:1 in favor of the double-tailed coin, so the posterior probability is (32/(32+1)=32/33). Double-checking that logic helps avoid silly mistakes under pressure.