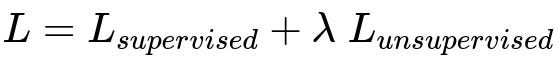ML Interview Q Series: In a semi-supervised learning scenario, how do you balance unsupervised and supervised cost terms during training to ensure both signal sources are utilized effectively?
📚 Browse the full ML Interview series here.
Hint: Typically done with a tunable weight or a curriculum strategy
Comprehensive Explanation
Balancing unsupervised and supervised signals is crucial in semi-supervised learning because one must leverage the limited labeled data while also extracting meaningful information from unlabeled data. The key idea is to form a joint objective function that combines a supervised loss term and an unsupervised loss term in a controlled manner. The major challenge is to find the right trade-off so the model does not overly rely on potentially noisy or uninformative unsupervised signals, while still reaping their benefits for representation and decision boundary refinement.
A common way to achieve this trade-off is to construct a loss function that integrates both terms. One typical approach is to introduce a tunable hyperparameter that scales the relative strength of the unsupervised term with respect to the supervised term. This can be expressed by a combined loss function:
In this expression, L_supervised is a loss computed using the labeled examples (for instance, cross-entropy if it is a classification problem), and L_unsupervised is derived from unlabeled data (for example, a consistency regularization loss, reconstruction loss, or other unsupervised objective). The scalar lambda is a hyperparameter that adjusts how heavily we emphasize unlabeled data’s contribution.
The parameters in the formula can be explained in plain text:
L_supervised is typically computed by comparing the model’s predictions to the ground-truth labels for the labeled subset. This ensures that the model maintains correctness on known categories or continuous target values.
L_unsupervised is derived from the unlabeled examples. For instance, one can use techniques like consistency regularization, where the model’s predictions on unlabeled data are enforced to be consistent under small perturbations, or use an autoencoder-like reconstruction objective.
lambda is the balancing coefficient that controls the influence of L_unsupervised relative to L_supervised. A high lambda value makes the learning process rely more on unlabeled data and can potentially overpower the supervised term. A low lambda value makes the unsupervised component negligible, causing the system to revert to a purely supervised learning approach.
There are several strategies to choose lambda. One direct approach is to treat it as a fixed hyperparameter and tune it using a validation set. Another approach is curriculum learning or dynamic weighting, where one starts with a lower weight on L_unsupervised and gradually increases it as training progresses. The intuition is that early in training, the model parameters can be highly inaccurate, so strongly using unsupervised loss might mislead the model. Once the model’s supervised learning is more stable, it can handle and learn more effectively from unlabeled samples.
When done properly, this semi-supervised framework can significantly enhance model performance, especially in cases where labeling is expensive or difficult, but unlabeled data is abundant.
Practical Implementation Details
In practice, one might combine supervised and unsupervised signals in code. Below is a conceptual example in Python using PyTorch syntax to illustrate how to implement a combined loss approach:
import torch
import torch.nn as nn
import torch.optim as optim
# Assume we have a model that outputs predictions for classification
model = MyModel()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
# Suppose we have a labeled batch (X_labeled, y_labeled) and
# an unlabeled batch X_unlabeled
criterion_supervised = nn.CrossEntropyLoss()
def unsupervised_loss_function(predictions_unlabeled):
# Example: a consistency regularization approach could
# penalize the difference in model outputs under small perturbations
# For illustration, assume an existing function:
return some_consistency_regularization_loss(predictions_unlabeled)
lambda_value = 0.5 # Could be tuned or updated via a schedule
# Forward pass on labeled batch
logits_labeled = model(X_labeled)
loss_supervised = criterion_supervised(logits_labeled, y_labeled)
# Forward pass on unlabeled batch
logits_unlabeled = model(X_unlabeled)
loss_unsupervised = unsupervised_loss_function(logits_unlabeled)
# Combine losses
loss_combined = loss_supervised + lambda_value * loss_unsupervised
# Backpropagation
optimizer.zero_grad()
loss_combined.backward()
optimizer.step()
The above snippet demonstrates how a single scalar lambda_value can adjust the relative influence of the unlabeled data component. In practice, one would typically iterate over a range of lambda values or apply a dynamic scheduling technique to find the best setting.
Follow-up Questions
How do we choose the value of lambda in practice?
One can experiment with different lambda values through a standard hyperparameter search strategy such as grid search or Bayesian optimization. The best value is usually the one that maximizes performance on a validation set that contains some labeled data. Alternatively, some methods rely on heuristic-based scheduling, where lambda is set to a low value initially and gradually increased as the model becomes more confident in its predictions.
Why might we want to use curriculum learning in semi-supervised settings?
Curriculum learning helps the model to first rely more on the reliable supervised signals, preventing it from being confused by possible noise in the unsupervised component early on. Over time, as the model’s supervised accuracy stabilizes, the unsupervised term can be gradually increased to ensure the model pays more attention to unlabeled data, thus refining its internal representation and decision boundaries.
Are there situations where supervised loss might overshadow unsupervised loss?
Yes, if lambda is set too low, the model might almost ignore the unlabeled portion and end up as a purely supervised model. Additionally, if the supervised data is extremely rich or large compared to the unlabeled set, the unsupervised component might have relatively little impact. Practical tuning is necessary to ensure that L_unsupervised is sufficiently weighted to provide a tangible benefit.
Are there more advanced techniques than a simple fixed weighting?
Yes, there are dynamic or adaptive weighting strategies, sometimes based on the model’s confidence on unlabeled samples or the distribution of predicted classes. Another approach is to employ confidence thresholds and only include unlabeled samples in the unsupervised loss if the model is sufficiently confident. Methods like pseudo-labeling also attempt to automatically generate labels for high-confidence unlabeled data and include them in the supervised loss term.
What are some typical pitfalls or edge cases?
One pitfall is when unlabeled data are drawn from a different distribution than the labeled data (domain mismatch). In that case, forcing the model to learn from unlabeled data that are off-distribution can hurt performance. Another edge case arises if the unlabeled data contains a large portion of noisy or random samples. The model might learn incorrect representations if the unsupervised objective is heavily emphasized. Proper data validation and outlier detection can mitigate these issues.
Can this approach fail if the unsupervised task is not closely aligned with the desired supervised objective?
It can. For example, if one chooses a reconstruction objective for the unsupervised loss, but the classification task relies on higher-level abstract features, the unsupervised objective might not help and could even lead to contradictory learning directions. Ensuring that the unsupervised objective is somewhat aligned with the downstream task is important. Consistency regularization or pseudo-labeling methods are typically more aligned with classification or regression tasks than a purely generative reconstruction approach.
How can one handle different scales of L_supervised and L_unsupervised if they differ by orders of magnitude?
In some problems, the magnitudes of the supervised and unsupervised losses might be very different. Normalizing each component by an estimate of its variance or by using techniques like gradient norm clipping can help. Another strategy is to rescale each loss term separately before combining them. For instance, one can standardize each loss term to a comparable range before summing them up.
Could you summarize an effective approach to balancing these terms in real-world scenarios?
A pragmatic method is to pick a range of lambda values (like 0.1, 0.5, 1.0, 2.0) and see which yields the highest validation performance. If the best lambda is on the boundary of the tested range, expand your search. If you have enough resources, add a dynamic strategy: start from a small value of lambda and ramp it up slowly until you see diminishing returns on a validation set. Ensure that the unlabeled data is from the same or a very similar distribution to the labeled data. Use modern consistency regularization or self-training frameworks to ensure that the unsupervised objective is relevant to the target task.
Below are additional follow-up questions
How do we handle catastrophic forgetting when balancing supervised and unsupervised learning?
Catastrophic forgetting can occur when a model trained on a particular distribution or combination of tasks forgets previously learned information once new tasks or distributions are introduced. In semi-supervised learning, this might happen if there is a shift in focus between the supervised and unsupervised components over time.
One strategy is to use elastic weight consolidation or similar regularization methods to preserve important weights for the supervised objective while still updating the model to learn from unlabeled data. Another approach is to maintain a replay buffer of labeled examples and occasionally re-train on these examples to reinforce the supervised signal. When employing a curriculum or dynamic weighting strategy, one should be cautious that increasing the unsupervised weight too rapidly does not diminish the importance of the labeled samples. Monitoring validation metrics and checking performance against a small hold-out set throughout training can provide a safeguard against forgetting.
A subtle, real-world issue is that if the unlabeled data distribution shifts over time (for example, new data coming from slightly different conditions), the model might adapt to the new unlabeled distribution and degrade performance on the original labeled data. Continual learning frameworks or incremental learning techniques can help mitigate this by periodically revisiting previously learned tasks or distributions.
If the labeled dataset is extremely small, how do we prevent the supervised portion from being overshadowed by the unsupervised portion?
When the labeled dataset is very small, there is a risk that the strong signal from a large unlabeled dataset overwhelms the limited supervised signal. One primary solution is to keep the unsupervised weight relatively low at the initial stages of training. That ensures the network’s parameters do not diverge in directions that contradict the small but critical labeled data. Over the course of training, if the model starts to generalize well on the labeled set, one can gradually ramp up the unsupervised term.
Selecting more reliable unsupervised objectives, such as consistency regularization that enforces stable predictions under small perturbations, can help. If the unlabeled dataset is extremely large, building a high-quality filtering or pseudo-labeling process is crucial. For instance, only incorporate unlabeled samples with high-confidence pseudo-labels into the supervised component. This prevents potentially misleading or noisy unlabeled examples from dominating parameter updates. Another subtlety is to ensure that your labeled data is representative of the same distribution as the unlabeled data; if not, the small labeled set might not effectively constrain the model’s learning on the unlabeled portion.
Are there differences in approach between classification and regression for balancing the two loss terms?
Yes. In classification, the unsupervised component often uses consistency regularization—pushing the model to output the same class for unlabeled data under various augmentations. Pseudo-labeling is another popular technique: the model assigns a class label to unlabeled samples if it has high confidence, then treats those samples as if they were labeled. This works well if the underlying problem is discrete and the model’s confidence calibration is reasonable.
In regression tasks, the continuous nature of predictions makes it more challenging to apply consistency regularization or pseudo-labeling. The model can produce a range of continuous outputs for the same input, and a naive threshold-based pseudo-labeling may not be as straightforward as in classification. Instead, techniques such as learning embedding consistency or using autoencoder-style reconstruction could be employed. Additionally, one might rely more on regularization methods that penalize the model for large changes in predicted values under small input perturbations.
A subtlety is that error metrics (like mean squared error for regression) could be more sensitive to outliers. If unlabeled data contains unusual values, a high unsupervised weighting might bias the model. Thus, for regression tasks, robust data filtering or explicit outlier handling might be essential before integrating unsupervised signals.
How does the choice of unsupervised objective affect generalization performance?
The unsupervised objective determines the features the model learns from unlabeled data. For instance, a reconstruction-based loss tends to encourage capturing information necessary to rebuild the original input, leading to strong low-level features that might not directly help the final supervised task. Meanwhile, consistency regularization focuses more on producing stable predictions under perturbations, often aligning better with classification tasks where decision boundaries must be robust.
Another element is that some unsupervised objectives (e.g., contrastive learning) emphasize learning discriminative representations. Such representations can generalize well if the unlabeled distribution matches the labeled distribution. If the unlabeled data distribution differs, certain spurious correlations might be encoded, hurting performance on the main task. One must ensure that the chosen unsupervised objective is aligned with the supervised goal to avoid forcing the model to learn irrelevant features.
Could the model learn spurious correlations from unlabeled data if it is not carefully balanced with supervised data?
Yes. If unlabeled data is biased or includes confounding factors, the unsupervised objective could push the model to latch onto patterns that do not generalize to the real supervised distribution. For instance, if the unlabeled data comes from different demographics or different lighting conditions in image tasks, the model might overfit to these domain-specific features and degrade performance on the labeled domain.
One way to mitigate this is through domain adaptation techniques, which attempt to align the distributions of the labeled and unlabeled data. Another strategy is to combine domain-specific knowledge or feature engineering that can filter out known confounders in unlabeled samples. Monitoring performance on a small validation set that matches the distribution of the labeled data is critical to detecting whether the model is relying on spurious signals.
If we suspect a distribution shift in the unlabeled data, how do we address it?
When the unlabeled data distribution differs from the labeled data distribution, directly combining L_supervised and L_unsupervised can be detrimental. One approach is to apply domain adaptation methods that transform unlabeled data closer to the labeled data domain. For instance, if you have images from different camera sensors, you might apply a style-transfer approach to unify them. Alternatively, re-weighting samples from the unlabeled dataset to match the distribution of the labeled dataset can help.
Adaptive weighting of unlabeled data can also mitigate distribution shifts: the model can down-weight samples that appear too far from the labeled distribution. If the shift is extremely severe, more advanced strategies such as adversarial domain adaptation or multi-task learning might be required, where the model learns features that are both discriminative and domain-invariant. A subtlety is that distribution shift can be partial—only some unlabeled samples are problematic. Identifying which subsets of the unlabeled data are in-distribution is often a practical step to reduce detrimental effects.
How do these semi-supervised approaches compare with purely supervised or purely unsupervised methods in terms of training stability?
Semi-supervised methods often have more potential sources of instability: they must reconcile potentially conflicting objectives from labeled data and unlabeled data. Purely supervised models do not face this conflict and are usually stable as long as the labeled set is sufficient. Purely unsupervised models do not have the ground truth labels to constrain them, so they can wander in feature space without guaranteeing performance on a downstream supervised task.
When implemented with the correct hyperparameters and a balanced weighting strategy, semi-supervised methods can achieve better performance than purely supervised methods, especially when labeled data is scarce. However, the risk is that inappropriate weights, poor unlabeled data quality, or domain mismatch can introduce instability and degrade performance. Techniques like consistency regularization or pseudo-labeling can help stabilize training by providing a clear, self-consistent goal for unlabeled data.
Training logs and validation metrics should be monitored carefully during semi-supervised training. If the model begins oscillating or if the validation performance drastically drops after adding more unlabeled signal, it might indicate an imbalance in the loss terms or a problem in the unsupervised approach.