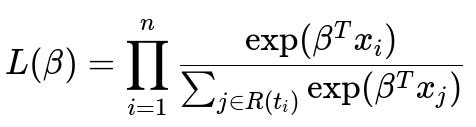ML Interview Q Series: In a survival analysis model, how would you adapt or design a cost function to handle censored data while still providing meaningful risk predictions?
📚 Browse the full ML Interview series here.
Hint: Methods like the Cox partial likelihood or extensions of rank-based losses.
Comprehensive Explanation
Censored data in survival analysis indicates that for some subjects in a study, we only know they survived up to a certain time without observing the actual event (e.g., death, equipment failure) after that time. Traditional loss functions designed for regression or classification do not straightforwardly handle such data because those typically assume the target variable is fully observed. To build a meaningful survival model, we need to adapt or design a cost function that accommodates these censored instances in a principled way.
Cox Partial Likelihood Approach
One prominent method is the Cox Proportional Hazards (PH) model, which bypasses the need to specify the baseline hazard function explicitly. Instead, it focuses on modeling the relative risk or hazard. The Cox partial likelihood captures how likely an event i, which occurred at time t_i, has a higher hazard than other individuals still “at risk” (i.e., those who have not yet experienced the event or been censored) at t_i.
Below is the core partial likelihood formulation for the Cox model. This partial likelihood is commonly used as the objective function (or, in practice, we minimize its negative log form) to handle censored data in a statistically sound way.
Where i runs over each subject that actually experienced the event (non-censored) in the dataset, n is the total number of such events, x_i is the covariate (feature) vector for the i-th event, and R(t_i) is the “risk set” at the event time t_i (i.e., the set of all subjects who are still under observation and have not yet experienced the event by t_i). The vector beta represents the parameters of the model we aim to learn.
A crucial advantage of this partial likelihood is that the censored subjects still contribute to the risk set until the time they are censored. The events that happen later than a censored time are not strictly contradictory to that censored observation because we do not know the actual event time for the censored subject; the censored subject is simply removed from the risk set once they are no longer observed.
Extensions and Rank-Based Losses
For neural networks or non-linear survival models, alternative loss functions that rely on ranking or pairwise comparisons can be employed. Examples include the Cox partial log-likelihood extended to neural networks and rank-based losses like the pairwise log-rank loss. These approaches share the same guiding principle: preserving the relative ordering of risks (or hazard) rather than pinning down exact survival times.
Rank-based methods typically handle censorship by only comparing ordered pairs where at least one subject has an observed event, effectively ignoring pairs that are completely censored in a way that no ordering information can be extracted. This preserves as much information as possible without violating what is unknown due to censorship.
Practical Implementation Strategies
In practice, implementing survival models with these specialized objectives often involves frameworks or libraries that already incorporate partial-likelihood or rank-based survival losses. For example, using lifelines in Python for traditional Cox models or adopting PyTorch or TensorFlow for neural network variants of survival analysis. One can implement a custom training loop where the negative log partial-likelihood is computed for each batch. Alternatively, for rank-based losses, you might use a pairwise margin ranking loss that only considers valid pairs where the event time ordering is known.
Below is a simplified illustration of how you might implement a partial-likelihood-like objective in PyTorch (though not exactly the canonical Cox partial-likelihood, it shows the general structure for a batchwise approach):
import torch
import torch.nn as nn
class CoxPHLoss(nn.Module):
def forward(self, risk_scores, events, durations):
# risk_scores: model output, shape [batch_size]
# events: 1 if event occurred, 0 if censored
# durations: time of event or censoring
# Sort by descending risk_score (or ascending if you prefer)
# so that partial likelihood can be approximated or computed in some fashion
sorted_idx = torch.argsort(risk_scores, descending=True)
sorted_scores = risk_scores[sorted_idx]
sorted_events = events[sorted_idx]
sorted_durations = durations[sorted_idx]
# Here, we would create a form of partial likelihood
# We won't detail the entire computation, but typically it involves:
# 1) Summation of log(risk score_i)
# 2) Subtraction of log of sum of risk scores in the risk set for each event i
# This is a placeholder to show the structure
log_partial_likelihood = torch.zeros_like(sorted_scores)
# Some computations for partial likelihood...
# ...
loss = -torch.sum(log_partial_likelihood) # negative log-likelihood
return loss
In real implementations, especially for large datasets, efficient algorithms are needed to handle the summations for the risk sets. Libraries that implement these methods typically maintain clever data structures or use sorting-based algorithms to avoid naive summation over all pairs repeatedly.
Follow-Up Question: How do we handle ties in event times?
When multiple events occur at the exact same time point, the risk set computations become less straightforward. Ties in event times mean the ordering among those subjects is not well-defined. Methods like the Breslow approximation or the Efron approximation are commonly used to handle these ties. The Efron method partitions the partial-likelihood calculation in a way that partially accounts for the fact multiple subjects had the same event time. It does so by averaging out the contribution of tied events in the denominator. The Breslow method is a simpler approximation that lumps tied events together in one step, though the Efron method is often considered more accurate.
Follow-Up Question: Are there any pitfalls or assumptions behind the Cox partial likelihood?
Yes, the Cox model makes the proportional hazards assumption. This assumption states that the ratio of hazard functions between two individuals is constant over time. Violations of this assumption (e.g., time-varying effects) can degrade the performance of the model. One might check for time-varying effects by testing interactions with time or applying more flexible modeling approaches (like time-varying covariates or piecewise models) to mitigate these violations.
Follow-Up Question: Could we incorporate deep learning with partial-likelihood?
Neural network extensions of CoxPH exist and are often referred to as DeepSurv or similar. The core idea is the same: pass input features through a neural network to get a risk score, and then plug that into the partial-likelihood. During training, we optimize the network parameters to maximize the Cox partial-likelihood (or minimize its negative log). This approach can capture complex non-linear relationships in the data while retaining the handling of censored observations via partial-likelihood.
Follow-Up Question: What about ranking-based losses like C-index?
The Concordance index (C-index) is used to evaluate the ordering quality of predicted risks relative to actual survival times. It can also function as a training objective (though it’s more common as a performance metric). The model tries to maximize the probability that for any two individuals with different event times, the one with the shorter time is predicted to have a higher risk score. This approach inherently deals with censorship by only considering pairs where the ordering can be ascertained (i.e., at least one event time is known and actually observed).
However, optimizing the C-index directly can be more computationally complex and less stable than using partial-likelihood-based approaches. Hybrid strategies exist: for instance, you might train with the Cox partial-likelihood and tune hyperparameters or model structures to optimize the C-index on a validation set.
Follow-Up Question: Could we adopt fully parametric approaches?
Yes, parametric survival models (e.g., Exponential, Weibull) specify a functional form for the baseline hazard and then incorporate censorship in the log-likelihood by treating censored data as those that only contribute a survival function term up to the censoring time. While this can work well, it imposes stronger distributional assumptions on the underlying survival times. The Cox model avoids specifying a functional form for the baseline hazard, making it semi-parametric and more flexible in that sense.
Follow-Up Question: How do you validate or evaluate a survival analysis model?
Common ways to evaluate include:
Concordance index (C-index) to measure the predictive ranking quality of risk scores versus observed times.
Integrated Brier Score to assess the overall calibration of predicted survival probabilities over time.
Visualization with calibration plots or predicted survival curves at various time intervals, checking how they match actual events.
Handling censorship in these metrics often involves only including pairs or intervals that provide definite time-to-event information.
These measures ensure the model not only fits well to the observed data but also generalizes effectively to new censored observations, providing meaningful risk predictions in real-world scenarios.
Below are additional follow-up questions
In a real-world scenario with time-varying features (covariates), how do we incorporate them into a survival model that uses partial-likelihood or other advanced cost functions to handle censored data?
Time-varying covariates are often critical in survival analysis. For instance, a patient's blood pressure or biomarker levels can change over time, and the risk is more accurately predicted by using these dynamic measurements rather than a single baseline measurement.
In a traditional Cox Proportional Hazards model, one approach is to treat each time-varying segment as a separate observation. Whenever a feature changes, you “split” the subject’s record at that time point. Each record indicates the interval during which the covariate values are (approximately) constant. This leads to multiple rows per subject, each with a start time and end time for that interval, along with the corresponding covariates. The partial-likelihood is then calculated in a piecewise manner, treating each interval as if it were a separate (but correlated) observation. A subject who gets censored at time t c contributes partially to all intervals that end prior to t c and partially to the interval that is ongoing at t c.
One must ensure that creating too many splits does not unnecessarily inflate data size and cause computational overhead. If features are recorded at very high frequency, you may need strategies for smoothing or aggregating those values (e.g., average or last-known values over certain time windows) so that your partial-likelihood or rank-based approach remains tractable.
A crucial subtlety is that the partial-likelihood implicitly assumes a Markov-like property in how covariates change. If the changes are abrupt and happen at random intervals, there is a risk of model misspecification. Another pitfall is that the proportional hazards assumption (that the ratio of hazards is constant over time) can become even more strained in the presence of certain types of time-varying data. Checking or relaxing that assumption (e.g., by adding time-by-covariate interactions) can be key in these settings.
How do you handle data with competing risks, in which the subject might have multiple possible events, not just a single event type?
In competing risks situations, a subject can experience one of several different event types, and experiencing one event type can preclude experiencing another. For instance, a patient could die from disease A or disease B, and once they die from A, the risk of dying from B is essentially moot. Classic Cox models do not immediately address this scenario because they assume a single type of event.
To tackle competing risks, one approach is the cause-specific hazards model. You fit a separate model for each event type, treating all other events as censoring. Another approach is the Fine-Gray subdistribution hazards model, which targets a subdistribution hazard function, allowing direct estimation of cumulative incidence for each event type. Each model can still handle censored data, but the definition of “censoring” gets nuanced. For example, in cause-specific modeling, an event of type B censors the subject for event type A.
Edge cases arise when one event type is extremely rare: the model for that event may have few actual observations and produce high-variance estimates. Another pitfall is failing to realize that cause-specific hazards and subdistribution hazards answer different scientific questions. Cause-specific hazards measure the instantaneous rate of each type of event among those still event-free, while subdistribution hazards measure how the proportion of one specific event changes among the entire original population over time. Depending on the research or product use case, choosing the right model for the question is crucial.
In practice, how can we handle a large portion of censored data in a dataset (e.g., 80% censored) and only 20% have observed events?
A high censoring rate can complicate survival analysis because the effective signal about actual event times diminishes. Traditional partial-likelihood approaches (like Cox) still remain valid because censored instances contribute to the risk set, but the statistical power is lower. That means the model might fit well to the minority of observed events yet carry substantial uncertainty in predictions.
A common pitfall is interpreting the model as if its confidence in the risk predictions is high when, in fact, large-scale censoring typically inflates confidence intervals for parameter estimates. Additionally, if censoring is informative (i.e., subjects are censored for systematic reasons), it biases hazard estimates. For instance, if highly at-risk subjects drop out of a study early, the model might underestimate the overall risk.
To handle this, strategies include:
Implementing sensitivity analyses by artificially adjusting the censoring times or simulating events to see how robust the model is under different assumptions.
Incorporating parametric or Bayesian approaches that allow incorporating prior information or partial knowledge about the time-to-event distribution.
Using specialized techniques such as inverse-probability-of-censoring weights if censoring is believed to be non-random and you can estimate the censoring mechanism.
These methods can strengthen the model’s robustness when faced with high censoring. However, one should be aware that no method can fully recover from extremely high censoring if insufficient event information is available.
If there’s a high class imbalance in terms of the fraction of events versus censored data, how do we adapt cost functions or training strategies?
In many survival datasets, only a small fraction of subjects might experience the event (e.g., system failures in a high-reliability product). This creates a different but related imbalance problem: the partial-likelihood or rank-based objective may overfit to the small portion of event records.
Potential strategies include:
Augmenting or reweighting the partial-likelihood. One might place a higher weight on event records during training so that the model pays more attention to the small number of observed events. This can be done by adjusting each term in the partial log-likelihood to reflect imbalance.
Using oversampling or synthetic event generation methods (conceptually similar to SMOTE in classification, but more tricky for time-to-event data). These might artificially inflate the number of events, though one must do so cautiously to avoid unrealistic survival profiles.
Considering parametric survival methods or Bayesian hierarchical models if prior knowledge about the distribution of event times can be leveraged. This can be beneficial when observed events are sparse.
A hidden pitfall here is that naive oversampling of event records can distort the risk set structure since each event is “tied” to a specific set of at-risk subjects at its event time. Over-counting certain events changes the partial-likelihood’s ratio terms incorrectly unless the risk sets are carefully re-weighted to remain consistent.
Could we adopt or design a parametric approach with a neural network, similar to distribution-based methods like Weibull or log-normal, while still accounting for censorship?
Yes. One can set up a neural network to predict parameters of a chosen distribution (e.g., the scale and shape for a Weibull distribution). Afterward, the likelihood function for time-to-event data (with appropriate modifications for censored observations) can be used as the training objective. Specifically, a subject with an observed event has a likelihood component corresponding to the probability density at that event time. A censored subject contributes the survival function evaluated at the censoring time. The combined likelihood across all subjects becomes the training objective.
For example, if T is Weibull-distributed with scale lambda(x) and shape k(x), the density is T^(k(x)-1) multiplied by an exponential factor (depending on x). You can then compute the cumulative distribution function for censoring. The neural network outputs lambda(x) and k(x) for each subject, and you optimize the log-likelihood or negative log-likelihood accordingly. This is sometimes called a deep parametric survival model.
Pitfalls include:
Choosing an inappropriate distribution can lead to systematic bias if the real-world time-to-event does not align with that parametric form.
Overfitting can occur if the model architecture is large relative to the size of the dataset, especially if events are scarce.
Implementation complexity increases because you have to carefully handle the derivative of the survival function for censored subjects.
What if there is delayed entry in survival analysis (subjects enter the risk set after time 0)? How do we incorporate that into partial-likelihood or rank-based cost functions?
Delayed entry occurs when a subject effectively joins the study in progress. For example, if a patient enrolls in a trial 2 years after the trial has started, the subject was not observed (nor at risk) for the first 2 years. By the time they join, they either have survived up to that time or have not had the event.
To handle delayed entry in a Cox partial-likelihood framework, you restrict the risk set to only those subjects who were actually under observation at that time. For a subject i whose “entry time” is e_i, they do not contribute to risk sets before e_i. This means each event that happened before e_i should exclude subject i from its risk set. In some implementations, you must carefully account for this by having an entry indicator that is used when constructing risk sets.
A key subtlety is that if the reason a subject enters late is related to their underlying risk, you can introduce bias by ignoring that mechanism. This is known as left-truncation, and the partial-likelihood must be adapted to account for the fact that all subjects under observation at a given time have necessarily “survived” up to that time. If unaccounted for, parameter estimates might be distorted.
If we want to predict hazard rates or survival probabilities at multiple time points (as in a discrete-time survival analysis or a multi-time-step approach), how do we adapt cost functions or training strategies?
In discrete-time survival analysis, you divide time into intervals and model the hazard (or survival probability) for each interval separately. For a neural network approach, you can output a probability for each interval that the subject transitions from the “alive” state to the “event” state. Observed events in interval j produce a likelihood term for that interval, while intervals prior to j indicate survival (and thus contribute a survival factor). Censored records contribute partial information up to the last observed interval.
Training can use a likelihood function summing across intervals:
A subject who experiences the event in interval j contributes a term for surviving intervals 1 to j-1 multiplied by the probability of event in j.
A subject censored in interval c contributes a term for surviving intervals 1 to c.
Potential pitfalls:
Binning the time domain can introduce boundary effects if intervals are chosen too coarse or too fine. Inappropriate interval width can degrade predictive accuracy or computational efficiency.
For heavily skewed data, certain intervals might have almost no events, leading to numerical instability in the model estimates.
Over-parameterization is possible if the network predicts a separate hazard parameter for each time interval. This might require regularization or smoothing constraints on how hazard rates evolve across intervals to avoid erratic predictions.
Are there any special considerations for cross-validation or bootstrapping to properly handle censored data?
When performing cross-validation or bootstrapping with censored data, you must ensure the structure of time-to-event information is preserved. In standard cross-validation, you might randomly shuffle the data and split it into folds. However, in survival contexts, a patient who is in the test fold should not appear in the training fold in partially truncated form, as it can leak future survival information.
One strategy is “temporal cross-validation,” where you split data by time intervals so that the test data always corresponds to later times than the training data. Another approach is subject-wise separation, ensuring no subject’s partial record leaks into the training set. If you do block bootstrapping, you resample entire subject trajectories rather than single time points.
A subtlety is that you need to maintain correct risk sets. If a subject is entirely withheld for the test fold, the partial-likelihood in the training fold might shift due to the removal of that subject from the risk set at times they otherwise would be considered at risk. This effect can be small if the dataset is large, but it can matter for smaller cohorts or high censoring. Also, metrics like the C-index can be sensitive to how pairs are formed across folds. Careful design of the evaluation strategy is crucial to avoid artificially inflated or deflated performance estimates.
For large-scale survival data, partial-likelihood computation can be expensive. Are there approximate or more scalable approaches to compute or approximate the partial-likelihood or rank-based cost function?
Cox partial-likelihood requires, for each event time, summing (or exponentiating and summing) over all subjects at risk. If you have thousands or millions of subjects, this risk set computation becomes a bottleneck. Several approximation strategies exist:
Sorting-based approaches combine sorted subject data to update the risk set cumulative sums more efficiently, rather than recomputing them from scratch each time.
Mini-batch approximations sample subsets of subjects to approximate the full partial-likelihood. A typical approach is to sample event subjects along with a subset of non-event subjects at risk and use that to estimate the ratio in the partial-likelihood. This introduces some noise but greatly speeds up training for large-scale data.
Alternative ranking-based objectives, such as pairwise ranking losses, might be easier to scale with modern GPU-based frameworks, though one must ensure that event-time pair formation remains meaningful.
A potential pitfall is that approximations can introduce bias in the parameter estimates and degrade performance if the sampling is done poorly. For instance, if a mini-batch rarely includes older subjects who have survived a long time, the model might systematically underestimate hazard rates for late events. Proper stratified sampling or weighting can mitigate this problem.
How do we detect and handle outliers in survival data, especially if some subjects have extremely long or extremely short survival times?
Outliers in survival analysis might be subjects who experience the event almost immediately or remain event-free far beyond the typical observation window. If these outliers are valid data points, they can heavily influence the partial-likelihood or parametric models. They might also indicate data entry errors or unusual edge cases in real-world systems.
Typical strategies:
Log-transforming or some other monotonic transformation on time can reduce skewness. This helps parametric methods fit better if the raw time scale has heavy tails.
Using robust survival models that down-weight extreme residuals. For instance, robust partial-likelihood versions or Bayesian priors that assume heavier-tailed distributions for baseline hazards or random effects.
Conducting an outlier analysis to see if those points truly represent the population of interest. If not, you might treat them as separate sub-populations or remove them if they’re data errors.
A potential pitfall is overcorrecting, where you dismiss real but rare events as “outliers.” This can bias the model to ignore important but infrequent phenomena. Balancing real-world distribution complexity with effective modeling is often challenging, especially when engineering teams demand interpretability and stability in final predictions.