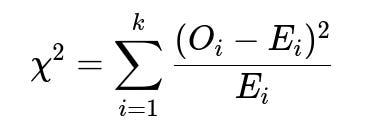ML Interview Q Series: In an A/B testing setup, what steps can be taken to confirm that participants are truly assigned randomly to each bucket?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Randomness in bucket assignment ensures that each participant has the same probability of ending up in any given group, thus minimizing systematic differences across test and control conditions. Below are key elements and methods to verify true randomness:
Checking Distribution of Key Features
One common way to validate random assignment is to compare distributions of important features (for example, demographics, historical behaviors, or other relevant covariates) across buckets. If the assignment is genuinely random:
Each group should look statistically similar in terms of average values of covariates.
Standard deviations or variance for numerical features should not differ significantly in any systematic way.
Any pronounced imbalance in covariates could signal a non-random assignment process.
Formal Statistical Tests
To rigorously verify that groups do not differ, you can use statistical significance tests. For categorical variables (for instance, gender or geographic location), a Chi-square test is frequently employed. For continuous numeric features (e.g., purchase amounts, time spent online), one might employ a t-test or ANOVA. If multiple features are tested, multiple comparison corrections might be needed.
Below is one of the most straightforward and critical formulae you might employ—the Chi-square test statistic for categorical data, often used to see if observed frequencies match what would be expected under a random (i.e., uniform or proportionate) distribution:
Where O_i is the observed count in bucket i, and E_i is the expected count in bucket i under the assumption of random assignment. The sum is taken over k buckets or categories. If the resulting Chi-square statistic is too large relative to the Chi-square distribution with the appropriate degrees of freedom, you may conclude that the differences in frequency are unlikely to be due to chance alone.
Practical Implementation Examples
A simplified Python snippet demonstrating a Chi-square test for verification of random distribution might look like this:
import numpy as np
import pandas as pd
from scipy.stats import chi2_contingency
# Suppose we have a DataFrame with a column 'bucket'
# that indicates which group a user belongs to (A, B, or C)
# and a column 'feature_group' (like 'region' or 'gender').
contingency_table = pd.crosstab(df['bucket'], df['feature_group'])
chi2, p_value, dof, expected = chi2_contingency(contingency_table)
print("Chi-square statistic:", chi2)
print("p-value:", p_value)
print("Degrees of freedom:", dof)
# The expected array gives the theoretically expected frequencies if distribution were random
print("Expected frequencies:\n", expected)
if p_value < 0.05:
print("Reject the null hypothesis: distribution may not be random.")
else:
print("Fail to reject the null hypothesis: distribution seems random.")
In practice, you would want to check multiple features (especially those known to influence outcomes) to ensure no systematic bias exists in bucket assignments.
Potential Confounders and Practical Pitfalls
Data Leakage: If the assignment logic uses a user or session identifier in a way that correlates with a demographic trait, your random distribution can be inadvertently skewed.
Multiple Testing: If you compare many features across groups, you increase the risk of false positives. Apply corrections (e.g., Bonferroni, FDR) if you are performing multiple hypothesis tests.
Sample Size: Small sample sizes can yield misleading results. Ensure you have enough participants in each bucket to provide valid test statistics.
Implementation Bugs: Even if the theoretical approach is correct, implementation or code bugs (for instance, reassignments or misapplied hashing) can result in non-random group membership.
How to Dig Deeper
Once you verify no serious imbalances in major user attributes, it is often wise to conduct further checks like ensuring no time-based patterns exist (e.g., everyone in the morning ends up in bucket A). You might also simulate random assignment in a test environment to confirm that the code used does indeed yield uniform distribution over many runs.
Possible Follow-Up Questions
What if my data is heavily imbalanced with respect to certain user attributes?
Heavily skewed data distributions (e.g., 95% of your users are from one region) can still appear random if there is no systematic bias in how that feature is assigned to buckets. In that scenario, you can focus on whether each bucket has about the same proportion of that majority demographic. The Chi-square test is still valid as long as your cell counts are not too small. Some guidelines suggest that all expected counts in your contingency table should be at least 5 for standard Chi-square approximations.
How do I confirm randomness in time-based or rolling deployment scenarios?
When implementing an A/B test that starts at a specific time and ends at a later time, you may worry about changes in traffic pattern or user traits. You could segment your data by time windows (e.g., daily or weekly bins) and verify that the bucket proportions stay consistent across those intervals. Additionally, a test on time-based segments can help detect anomalies where a certain day might have assigned more users to one bucket due to implementation errors.
Is a Chi-square test always the best way to validate randomness?
Not necessarily. For numeric or continuous variables, t-tests or nonparametric alternatives (Mann-Whitney U if distributions are skewed) might be more appropriate. The Chi-square test works best with categorical data to compare observed vs. expected frequencies. For verifying random assignment of a numerical variable, an ANOVA or Kruskal-Wallis test might be employed for multiple buckets.
What do I do if I fail the randomness check?
If you fail the randomness check (for example, the p-value is extremely small for multiple key features), you may have:
Bugs in the random assignment logic
Systematic user self-selection bias if participants can somehow choose their bucket
Issues with how you collected or segmented your data
You would need to investigate how users are being assigned, verify the code or system generating random IDs, and ensure no external factor is determining which bucket they land in.
In real-world systems, it is crucial to fix the assignment method, rerun the test in a controlled environment, and repeat the checks on a fresh sample.
Below are additional follow-up questions
How can hashing user identifiers sometimes create unexpected bias in bucket assignment?
When a system uses a hash function to determine which bucket a user should join, the assumption is that the hash outputs are uniformly distributed across the hashing range. In practice, certain hash implementations or certain user identifier structures can cause collisions or non-uniform distributions. For example, if a user ID pattern is highly correlated (like a timestamp-based ID or sequentially generated ID), the resulting hash might produce more collisions in specific ranges. If those specific ranges map to certain buckets, you will see a higher concentration of users in a particular bucket. These collisions can mimic or introduce a subtle bias that is hard to detect unless you do a thorough distribution check across buckets. To mitigate this, it is often good practice to:
Use cryptographic-grade hash functions (e.g., SHA-256) or well-tested uniform hashing algorithms.
Double-check the distribution of hashed values on a random sample of user IDs to confirm uniformity.
Validate that the code applying the hash is consistent across environments and that no locale or character-encoding issues lead to systematic skew.
Potential Pitfall: If you ever change the hashing algorithm during the experiment, you risk reassigning users to new buckets in the middle of the test, invalidating results.
What if certain groups of users can opt out or drop out from the test at different rates?
Even if the initial assignment is random, differences in group engagement might lead one bucket to have disproportionately high or low retention. For instance, if Bucket A has a user interface that is less appealing, more users might drop out or opt out early. This phenomenon does not necessarily mean initial assignment was non-random, but it can alter the effective sample composition over time, resulting in skew in the final dataset of “active participants.”
This can create a challenge when you analyze the data, because you might observe that Bucket A has fewer users by the end, or that it has systematically different types of users (e.g., highly tolerant or more tech-savvy). To handle such issues:
Monitor and compare dropout rates across buckets as part of your test hygiene.
Consider an “intent-to-treat” approach in which all assigned users remain in their buckets for analysis, regardless of whether they actively engaged to the end.
Explore if significant differences in dropout rates suggest a problem with the tested variant or confounding factors that might bias the results.
Edge Case: Sometimes, certain users may have system constraints (like older devices or particular browsers) that are more prone to errors or timeouts in one test variant, leading to hidden forms of dropout bias.
How do you validate randomization in multi-armed or adaptive tests (e.g., bandit algorithms)?
In a multi-armed bandit setup, the proportion of traffic assigned to each variant (or “arm”) is not fixed. The algorithm dynamically updates the assignment rates based on performance metrics, typically shifting traffic toward better-performing arms over time. Strictly speaking, such a process is not purely random assignment—there’s a feedback loop that skews sampling. If someone wants to confirm that the initial assignment is unbiased, you could check:
The earliest phase of the bandit algorithm (often called an “exploration phase”) when arms receive near-equal assignment.
The method used by the bandit to update probabilities (e.g., Thompson Sampling or Upper Confidence Bound). Confirm that the random draws or calculations used to allocate traffic are consistently applied and not impacted by external user features or sequences of user IDs.
However, once the bandit has enough data, assignments become intentionally biased toward higher-performing arms. If the question is specifically about verifying randomness within the exploration phase, you can still use standard checks like Chi-square or comparing distribution means across arms. For the adaptively allocated phase, the “randomness” is conditional on performance signals rather than purely random assignment, so classic randomization checks are less applicable.
Subtle Issue: If your bandit’s code inadvertently references user attributes to tune traffic allocation, you might systematically favor (or disfavor) certain user segments across arms without realizing it.
Could correlated user segments within the same bucket invalidate random assignment checks?
In real-world applications, users might come in clusters (e.g., corporate networks, family plans, or shared devices). If one large corporate network has thousands of employees, and its IP range all happen to land in a particular bucket, you lose the independence assumption. Although the assignment might still be random on an individual basis, the presence of a large correlated cluster in a single group can skew analyses and give the illusion that randomization is incorrect.
To address this:
Identify potential clustering factors like corporate IP addresses, device families, or related marketing campaigns.
Run random checks not just at the individual level but also at the cluster level, ensuring that major organizations or families of users are adequately distributed across buckets.
Consider hierarchical or cluster-aware assignment strategies if your domain frequently experiences such grouping.
Pitfall Example: If you simply do a hash on IP addresses rather than user IDs, you might end up with entire corporate networks in the same bucket. That would appear random on paper if your test is only counting unique IP addresses, but effectively you’ve broken the spirit of user-level randomization.
How do you spot partial randomization caused by layered or hierarchical assignment logic?
Often, large-scale systems use multiple layers of assignment logic. For instance, high-level logic might route 50% of overall traffic into the A/B test, and within that subset, there is a secondary randomization to multiple buckets. If the top-level funnel into the experiment is itself not random (say, it is assigned only to certain geographies or certain user types for cost or compliance reasons), then the final distribution among buckets is not truly random for the broader user population.
To diagnose such partial randomization:
Carefully map out the entire funnel of user assignment from the first filter to final bucket assignment.
Examine whether the “in test” user population is systematically different from the “not in test” population. If so, you have randomization only among a pre-selected sub-sample.
Use the same checks (Chi-square, t-tests) within each layer to ensure that every routing decision is, in fact, random with respect to relevant user attributes.
Real-World Scenario: A system might first filter by site region (e.g., US vs. non-US). Then only US users are split into A, B, or C. If your overall user base is 70% non-US, your final test groups do not represent 70% of those global users. So the buckets are random only within the “US user” slice.
How do I ensure that my randomization code works consistently across multiple languages or platforms?
In large organizations, different parts of the tech stack may be built in various languages (Python microservices, Java backend, JavaScript frontend). If your random assignment function is not consistently implemented—or if it uses distinct pseudorandom number generators with different seeds across environments—some users might inadvertently get different bucket assignments depending on which layer of code is triggered.
To reduce these risks:
Centralize the bucket assignment logic to a single service if possible.
If multiple systems need to replicate the logic, adopt a standardized approach to random number generation (for example, consistently using a 64-bit hashing routine on a canonical user ID).
Run cross-platform tests: pass the same user IDs through each system or language layer to confirm the final bucket assignment is identical.
Subtle Issue: Even if you have a “global seed,” programming languages can have different default behavior regarding integer overflow or floating-point rounding. Make sure your test suite captures these potential differences.
How should I handle randomization checks when a small fraction of traffic is allocated to the A/B experiment?
Sometimes you only expose, say, 1% of your total traffic to the experiment in a staged rollout or canary testing approach. Even if the assignment method is random, that small fraction might not have enough data to produce stable distribution checks. Standard significance tests can fail to detect small but meaningful differences in sub-groups when the sample size is limited.
Suggestions to mitigate this:
Accumulate enough data over a sufficient period. The smaller the sample fraction, the longer you might need to run the experiment to gather reliable evidence of random assignment.
If feasible, conduct an initial random check on a larger sample for a shorter time window, then scale back to your 1% canary approach.
Focus on high-level user attributes that are critical to your product metrics to ensure those subgroups are not drastically skewed.
Edge Case: If your site traffic is extremely heterogeneous (e.g., seasonal fluctuations, major marketing campaigns), even the day-to-day baseline might shift, making it even harder to confirm random distribution with a tiny fraction of traffic.
Does randomizing each visit or session (instead of each unique user) affect verification of random assignment?
When randomization occurs at the session level—meaning each session or visit might be assigned to a different variant—this can inflate your sample size artificially and complicate analysis. You might see that the same user on multiple sessions is assigned to multiple buckets over time, which can undercut the idea of a stable “treatment experience” for that user.
If you intend to measure user-level metrics (like long-term user retention), session-based randomization is not always appropriate because the same user experiences different conditions across visits.
For verifying session-level randomization, you can check that each session is equally likely to fall into each group. This might still appear random, but the aggregated user-level data could be confounded by repeated measures from the same user.
Always align your randomization unit with how you plan to measure success. If your success metrics are user-level, do user-level randomization. If your success metrics are session-level, session-based randomization is more appropriate.
Potential Pitfall: If your analytics pipeline merges all sessions from a given user into a single row for analysis, you may lose track of which sessions belonged to which bucket, causing mixing of test conditions and misleading results.
How can you account for cross-device or cross-channel scenarios in randomization?
Users nowadays access products from multiple devices (mobile, desktop, tablet). If your randomization only tags a single device or browser and not the user’s account, a user might end up in different buckets when switching from phone to laptop. This dilutes the “treatment effect,” as the user doesn’t consistently experience one variant. Conversely, if you unify by user account, then you risk losing data from logged-out sessions or multiple household members sharing the same account.
In these multi-device or multi-channel contexts, be mindful that:
Unifying the randomization at the user account level typically gives the cleanest test of user-level outcomes (like conversion or churn).
If you are measuring device-specific metrics (like a mobile app feature test), it can be acceptable to randomize at the device level, but you must note that a user might see different experiences on different devices.
Validate that the hashing or randomization logic is consistent across device platforms and that you are not inadvertently double-counting or skipping certain device types.
Edge Case Example: A user who shops on a mobile browser while logged in, then on a desktop browser while not logged in, can appear as two distinct “users” to your system. Make sure you have a stable strategy for deduplicating or merging these situations if your test demands user-level random assignment.
In what ways can user geography or local regulations interfere with random assignment?
Certain countries or regions may have data usage or privacy regulations that limit your ability to track or store user identifiers. If you cannot reliably store or process an identifier for a group of users, you might be forced to default them all into one bucket (e.g., a “control” group) for compliance reasons. This approach can undermine the uniform assignment principle. Additionally, certain local laws might restrict the types of A/B tests you can run or require special disclaimers, leading to a non-random subset in certain geographies.
To handle this:
Work with legal teams to understand data governance policies in each region, ensuring that your randomization plan does not violate any local rules.
If forced to exclude or treat a geographic region differently, separately track that region so as not to pollute your main experiment results.
Acknowledge that your test might only be truly random for the regions where you have full user ID coverage. This can limit generalizability of your final results to other geographies.
Pitfall: Unknowingly ignoring region-specific assignment constraints can lead to a spurious impression of random assignment overall, while in reality, your test is only random for a smaller subset of global users.