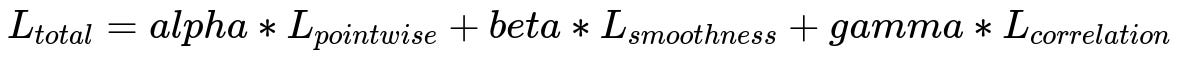ML Interview Q Series: In the context of time-series forecasting, what unique considerations go into choosing or designing a cost function (beyond standard regression losses)?

📚 Browse the full ML Interview series here.

Hint: Think about multi-step predictions, alignment in time, and correlation structures.

Comprehensive Explanation

Cost functions for time-series forecasting must account for the temporal structure of the data, potential correlations between predictions at different time steps, the need for multi-step forecasting, and alignment of forecasted outputs with true values over time. Standard cost functions like Mean Squared Error (MSE) or Mean Absolute Error (MAE) are often a starting point, but in time-series tasks, there are additional factors worth considering.

One critical aspect is handling multi-step predictions. In time-series scenarios, forecasts for future steps often depend on the predictions of previous steps, especially when rolling or iterative prediction is used. This dependency can amplify small errors over time and lead to large overall deviations. Therefore, a cost function might need to weigh different time horizons differently, penalize error accumulation across the forecast horizon, or incorporate correlations across multiple forecasted steps.

Alignment in time is also vital in many practical applications. If the forecast is shifted by a small amount in time but is otherwise correct in shape and magnitude, a simple pointwise MSE might harshly penalize such phase shifts. Some specialized metrics aim to measure similarity in shape rather than exact pointwise matching.

Additionally, time-series often exhibit serial correlations, seasonal patterns, or cross-correlations with other series. Designing a cost function might require incorporating these dependencies explicitly—for instance, by introducing terms that penalize deviation from known seasonal cycles or that consider correlation across multiple time-series channels.

Below are some considerations in detail:

Modeling Correlation Over Time Time-series observations are rarely independent. When the model’s predictions for one time step affect subsequent steps, a specialized cost function could explicitly include correlations. For example, it might use a penalty term that measures correlation mismatch between forecasted series and observed series.

Emphasizing Specific Time Horizons In certain applications, short-term forecasts are more critical than long-term ones (or vice versa). A weighted cost function can allocate higher weight to errors that occur in specific parts of the forecast horizon.

Shape- and Phase-Sensitive Errors Some tasks require that the predicted shape (trend, ups and downs) matches the true time-series more closely than strict pointwise matching. Techniques like dynamic time warping (DTW) are sometimes used to measure and penalize misalignment in the time axis.

Handling Multi-Output Forecasts When forecasting multiple time steps at once, a multivariate cost function might penalize both the marginal errors at each time step and the covariance structure across time steps.

Distributional Forecasting Often, especially in real-world scenarios, a point estimate is less informative than a predictive distribution over future values. Cost functions can be based on proper scoring rules (like the Continuous Ranked Probability Score) that measure the quality of the entire predicted distribution instead of just a point forecast.

Potential Follow-up Questions

What are the main drawbacks of using standard MSE or MAE for time-series forecasting?

One key drawback is their inability to account for temporal dependence in a time-series. MSE or MAE treats each time step as an independent entity, ignoring that errors made at earlier time steps may propagate to later predictions. This means an early forecast error can lead to larger errors downstream, yet MSE or MAE provides no additional penalty for compounding such errors. Additionally, these standard losses do not address alignment issues—where a small phase shift can cause disproportionately high errors if the predicted series is slightly out of sync with the observed series.

How can we incorporate multi-step predictions into a cost function?

One approach is to compute a cumulative error across multiple future time steps. For example, one might sum or average the errors at each forecast horizon, possibly applying different weights for different horizons. If y(t+k) is the ground truth k steps ahead and y_hat(t+k) is the corresponding forecast, one could define a weighted sum across K horizons in plain text as:

where alpha_k are non-negative weights (that sum to 1 or any desired factor), and L is a base loss like squared error. By carefully selecting alpha_k, one can place different emphasis on short-term vs. long-term errors.

Parameters: alpha_k represents the relative weight assigned to the forecasting error at horizon k. A higher alpha_k penalizes forecast errors for that horizon more heavily. L(y(t+k), y_hat(t+k)) is some basic loss measure (e.g., squared or absolute deviation) between the observed target y(t+k) and predicted y_hat(t+k) at step t+k.

Could we handle time shift or phase shift in a specialized cost function?

Yes. A common way to handle time or phase shifts is via a shape-based distance measure. Dynamic Time Warping (DTW) is a classic example, where you measure how well two temporal patterns match, even if they are out of phase for a few steps. One could use DTW distance (or a similar measure) as a cost function. However, DTW-based losses can be computationally expensive and may not be differentiable in a straightforward way, which can complicate gradient-based training. Some practitioners use approximate differentiable versions of DTW or combine DTW with standard losses to balance alignment with computational feasibility.

How do we incorporate seasonality or other domain-specific patterns into a cost function?

One practical approach is to include regularization terms or additional penalty functions that capture known patterns. For example, if there is a weekly seasonality pattern, one can add a term penalizing deviations from known cyclical behaviors. Another approach is to incorporate seasonality as extra inputs or features (e.g., day-of-week, month-of-year) into the model, though that would be part of the model architecture rather than the cost function itself. Some advanced methods might explicitly penalize incorrect seasonality amplitude or phase.

Why might correlation structure matter in time-series cost functions?

Time-series often exhibit autocorrelation (a correlation of the series with itself lagged by certain intervals) and cross-correlation (multiple related series moving together). A specialized cost function could penalize a mismatch in these correlation structures if the application requires the model to reproduce certain covariance or correlation patterns accurately. For instance, in financial forecasting of multiple assets, predicting correct correlations is as important as predicting individual asset movements.

How can we implement a custom cost function for time-series forecasting in Python?

Below is a simple code snippet demonstrating how you might implement a multi-step weighted MSE in PyTorch. This snippet assumes you already have predicted sequences and actual sequences in the shape [batch_size, forecast_horizon]. You can then compute a weighted MSE across the forecast horizon.

import torch
import torch.nn as nn

class MultiStepWeightedMSE(nn.Module):
    def __init__(self, weights):
        super(MultiStepWeightedMSE, self).__init__()
        self.weights = weights  # e.g., a tensor of shape [forecast_horizon]

    def forward(self, preds, targets):
        # preds and targets shape: [batch_size, forecast_horizon]
        # We calculate MSE at each horizon and then weight it
        # Expand weights to match [batch_size, forecast_horizon]
        mse_per_timestep = (preds - targets) ** 2
        weighted_mse_per_timestep = mse_per_timestep * self.weights
        loss = torch.mean(torch.sum(weighted_mse_per_timestep, dim=1))
        return loss

# Example usage:
forecast_horizon = 3
weights_tensor = torch.tensor([0.6, 0.3, 0.1])  # Heavier penalty on first step
criterion = MultiStepWeightedMSE(weights_tensor)

# Suppose preds and targets are shape [batch_size, 3]
preds = torch.tensor([[2.0, 2.5, 3.0],
                      [1.0, 1.5, 2.0]], dtype=torch.float32)
targets = torch.tensor([[3.0, 2.0, 4.0],
                        [2.0, 1.0, 3.0]], dtype=torch.float32)

loss_value = criterion(preds, targets)
print(loss_value.item())

In this example, the cost function sums the weighted MSE across the forecast horizon for each sample in the batch and then takes the average across the batch. This allows differential weighting of early and later time steps.

How do we handle probabilistic forecasts or predictive distributions?

Instead of returning a single point forecast, your model might output parameters of a distribution (for example, mean and variance if you assume a Gaussian). You could adopt a scoring rule such as the Continuous Ranked Probability Score (CRPS) that measures how well the predicted cumulative distribution function aligns with the observed value. Another popular approach is the Negative Log-Likelihood (NLL) of the target under the predicted distribution. By training the model to minimize NLL, you encourage it to output distributions that are likely to generate the observed time-series values.

In what scenario would a cost function that heavily penalizes extreme outliers be useful?

Certain time-series applications, such as load forecasting for power grids or anomaly detection in manufacturing processes, need to be extra cautious about large deviations. In these situations, we might turn to cost functions or weighting schemes that place disproportionately large penalties on significant forecast errors. This helps ensure that the forecasting model pays more attention to potentially high-risk events (like demand spikes or abnormal sensor readings) and can adjust predictions accordingly.

Could we devise a cost function that encourages smoothness in the forecasts?

Yes. If an application requires the forecast to be smooth (for instance, modeling physical processes where sudden jumps are unlikely), you can add a penalty term on the second derivative (or differences across consecutive time steps) of the predictions. For example, you could penalize the squared difference between adjacent time steps in the predicted sequence to reduce abrupt changes. However, such a term imposes assumptions about the underlying signal and might not be suitable for highly volatile data.

Is it possible to combine different penalty terms for various objectives?

Yes. In many real-world scenarios, it is common to combine different metrics or penalties in a single composite loss. You might mix a pointwise error term with a smoothness term, a penalty for incorrect correlations, or a term that accounts for time alignment. The final loss might look like:

Parameters: alpha, beta, gamma are hyperparameters balancing the different objectives. L_{pointwise} is typically MSE or MAE. L_{smoothness} can be the penalty that enforces smoothness in the predicted sequence. L_{correlation} can penalize differences in correlation structures between predicted and observed series.

Designing such composite loss functions requires domain knowledge to choose meaningful components and tune the relative weights so that the model optimizes the correct priorities.

Below are additional follow-up questions

How do we handle partial or incomplete time-series data and incorporate that in our cost function?

Incomplete time-series data often arise from missing observations, sensor failures, or sporadic logging. When designing or choosing a cost function, one pitfall is inadvertently ignoring the temporal structure by simply discarding rows with missing values. Dropping data can cause biased estimations or reduce training data volume significantly, particularly in long forecasting horizons.

One approach is to impute the missing data before computing the cost, for example via interpolation or more sophisticated methods such as a model-based imputer. A risk is that inaccurate imputation can propagate errors into the cost calculation. Another solution is to design a cost function that gracefully handles missing values by ignoring them or by applying a weighting mechanism that reduces the influence of uncertain or imputed data. For instance, if a time step is partially observed or has poor data quality, the cost function could assign a lower weight to the error from that point.

A subtle issue is that in certain domains (e.g., medical time-series), it might be informative that a measurement is missing—this can be correlated with the underlying state (such as hospital discharge or sensor malfunction). In such scenarios, the cost function might need to penalize a model’s lack of awareness that “no measurement” is itself a signal. If the model incorrectly treats missingness as random, the forecast could degrade. Thus, the solution requires a combination of domain knowledge, robust imputation (or explicit modeling of missingness), and a cost function that appropriately discounts or penalizes uncertain data.

In practice, how do we choose the best cost function for a given time-series forecasting problem?

The best cost function depends on the forecasting goal, domain requirements, and data characteristics. If minimizing large deviations is most critical (e.g., in risk management), a cost function that heavily penalizes outliers may be preferred. If alignment and general shape matching are key (e.g., matching cyclical patterns in manufacturing), a shape-based metric like dynamic time warping (DTW) or a composite loss that includes time-alignment terms might be more appropriate.

A common pitfall is defaulting to MSE or MAE out of habit, without fully considering the consequences for the downstream application. For instance, if under-forecasting is much worse than over-forecasting (say, for inventory planning), a quantile loss at a high quantile might be more suitable to ensure the model overestimates rather than underestimates demand. Conversely, for applications where distributional forecasts matter (e.g., energy load forecasting with high stakes), a probabilistic scoring rule like the Continuous Ranked Probability Score (CRPS) or Negative Log-Likelihood is more relevant.

An additional challenge is that certain cost functions are harder to optimize, especially in deep learning contexts. Non-differentiable or computationally heavy metrics (like DTW) may require specialized techniques or approximations. Therefore, one must balance practical constraints (e.g., training speed, gradient-based optimization) with the desire to reflect the domain-specific measure of forecast quality.

What are potential issues with overfitting to a specialized cost function in time-series forecasting?

When you design a highly specific cost function—perhaps giving strong penalties to a particular subset of errors—it can lead the model to overfit to those peculiarities. For instance, if we heavily penalize late detections of peaks, the model might systematically over-predict peaks to avoid that penalty, introducing bias into other aspects of the forecast.

Another subtlety is that a specialized cost function might not generalize to slightly different operational conditions. For example, if the environment changes (say, a new seasonality pattern appears), the model could behave poorly because it was over-optimized on the original distribution. Additionally, if we do not incorporate proper regularization or cross-validation, we risk optimizing heavily on the training set in a way that does not reflect real-world performance.

To mitigate this, careful validation on multiple data splits, as well as a sanity check against simpler baseline metrics, is important. It can be beneficial to use a composite approach that includes a standard baseline cost (like MAE) alongside specialized penalties so that the model does not completely disregard overall accuracy while it chases a narrower objective.

When do we prefer more robust losses, such as Huber or quantile-based losses, in time-series forecasting, and how do we interpret them?

Robust losses like the Huber loss are particularly helpful when the time-series data exhibit outliers or heavy-tailed distributions. In many real-world signals, spikes or extreme variations can occur unpredictably (e.g., unusual sales surges). Standard MSE is very sensitive to outliers, because squaring large residuals magnifies their impact. MAE handles outliers slightly better but can have less stable gradients when errors are near zero.

The Huber loss combines the benefits of both MSE (smooth for small errors) and MAE (less extreme penalty for large errors), making optimization more stable. Quantile-based losses (e.g., pinball loss) allow the model to learn a conditional quantile of the target distribution, which is useful if we want to forecast a high percentile (say, the 95th percentile) to ensure capacity planning for worst-case demand. Interpreting quantile forecasts means understanding that the model is trying to say “there’s a 95% chance the actual future value is below this forecast.” This can be very valuable in risk-averse domains or cost-sensitive scenarios where under-prediction is highly penalized.

A potential pitfall is that Huber or quantile losses may require additional tuning parameters (like the transition point in Huber) or knowledge of which quantiles are most relevant for your application. Without domain insight or proper validation, you may choose a quantile that does not align with your true operational needs.

How does the presence of external covariates (exogenous variables) affect the choice of cost function?

When time-series forecasting models incorporate external covariates—like weather, economic indicators, or promotional calendars—these additional inputs can change how we evaluate forecasts. If the external variables strongly explain some fluctuations in the target series, we might place more emphasis on periods where the model sees major shifts in covariates. For instance, if we know a severe weather event is imminent, we care that the forecast captures the resulting spike or dip correctly.

A potential edge case is that if the covariates themselves are uncertain forecasts (e.g., predicted weather rather than actual weather), errors in these covariates can propagate to the time-series predictions. The cost function might need to factor in the accuracy of the covariate forecasts, especially if they are imperfect. In such cases, a composite cost could penalize mismatch in the target time-series while also weighting the error that arises from inaccurate covariate predictions. Alternatively, one might adopt an end-to-end approach that includes the covariate prediction errors within the same framework, but that can complicate training and model interpretation.

Could we incorporate frequency domain considerations into a cost function? If so, how?

Yes. If a time-series has characteristic frequencies (e.g., cyclical components, periodicities), it may be useful to represent both the forecast and ground-truth series in the frequency domain and penalize discrepancies there. One approach is to apply a Fourier transform to both the predicted and actual signals over a given window, then compare the magnitudes or phases of the principal frequency components. A mismatch in dominant frequencies could be penalized more than smaller high-frequency noise components.

A potential pitfall is increased computational complexity, since frequency-based transformations require additional steps to compute. Another subtlety is that stationarity assumptions in the frequency domain might not hold if the time-series is non-stationary (for instance, if seasonalities change over time or new frequencies appear). One must also handle the edges of the forecast window carefully, as naive spectral analysis can produce artifacts at the boundaries. Lastly, optimizing a non-time-domain cost may not always be straightforward in typical gradient-based frameworks, and it might require custom backpropagation solutions.

How do we handle non-stationary time-series in designing or choosing cost functions?

Non-stationary time-series exhibit changing statistics (mean, variance, or seasonality) over time. A cost function designed for a stationary process might incorrectly assume that past errors or patterns carry the same weight throughout the series. For instance, if the scale of the time-series grows significantly over time, a standard MSE computed over the entire dataset may overweight the more recent, larger-valued errors compared to earlier errors.

One common approach is to use scale-invariant cost functions, such as Mean Absolute Percentage Error (MAPE), so that large values later in the series do not dominate the cost. However, MAPE can become unstable if the actual values are close to zero, so you might consider a modified version (like SMAPE, Symmetric Mean Absolute Percentage Error) or a piecewise approach.

Another strategy is to segment the time-series into more stationary chunks and compute the cost within each segment separately, then combine these partial losses. This approach requires domain knowledge to identify regime changes. If the non-stationarity is abrupt (like structural breaks), you may consider an adaptive or rolling cost function that focuses on the more recent data to capture the current regime. The main pitfall here is losing some long-term context if you rely only on local segments for your optimization.

How do we approach the problem if time-series data has irregular time steps when computing the cost?

In real-world applications, data might not be sampled at uniform intervals, leading to irregular or asynchronous time-series. Directly applying a typical cost function (like standard MSE) that compares index-aligned points can be misleading because it assumes a uniform time step.

One solution is to resample the time-series at regular intervals using interpolation or a suitable aggregator (e.g., the mean value in each time window). This resampled data can then be used in a standard cost function. However, if large gaps occur, interpolation may distort the signal, especially if the underlying dynamics are fast-changing.

Another method is to integrate the model’s predictions over continuous time (if it outputs a continuous function) and compare it to actual integrated observations. This approach can be more complicated to implement and optimize. Pitfalls include potentially large errors during large unobserved gaps that are never punished if the cost function only compares the integrated areas. Finally, if data are extremely sparse, it might be more meaningful to incorporate specialized methods that can handle time intervals explicitly, such as point process models or neural ODE-based solutions. The cost function in such scenarios must reflect the actual time difference between observed data points, ensuring the forecast aligns with the irregular sampling schedule.

What are potential numerical stability issues that might arise in time-series cost function implementations, and how can we mitigate them?

Numerical stability problems can manifest in different ways. One common example is overflow or underflow when computing error terms if the series contains very large or very small values. Another issue can occur when using percentage-based errors (like MAPE) and the time-series includes values near zero, causing division-by-zero or massive spikes in the loss.

To handle overflow or underflow, it is often useful to scale or normalize the series beforehand, so values lie within a reasonable range (e.g., between 0 and 1 or mean 0 and standard deviation 1). For MAPE, adding a small constant to the denominator helps avoid division-by-zero. If the model outputs distribution parameters for a probabilistic loss (like the variance term in a Gaussian), ensuring the predicted variance is bounded away from zero or negative values is crucial (e.g., by predicting the log-variance and exponentiating it).

Another subtlety is the accumulation of floating-point errors in some iterative forecasting methods, where each predicted step is used as an input for the next step. A small numerical inaccuracy can be magnified over multiple time steps. Using double precision or carefully clipping predictions at each step can help avoid compounding errors, although these approaches can increase computational costs.

Could we adapt reinforcement learning style cost functions in a time-series forecasting environment that is part of a control or decision-making system?

Yes, if the forecasts are directly linked to actions or decisions that are made in real-time (e.g., inventory orders, energy load balancing, supply chain decisions), we can adopt a reinforcement learning perspective. Instead of a purely supervised cost, we might define a reward function based on the net outcome of decisions informed by forecasts. For instance, the reward might account for the cost of being overstocked vs. understocked. The RL agent then learns to forecast in a way that maximizes cumulative reward, which could deviate from minimizing standard forecasting errors.

A pitfall is that in a pure RL approach, the system might find a policy that’s optimal for the given reward structure but suboptimal in terms of raw predictive accuracy. This can be acceptable if the ultimate goal is improved operational metrics (like profit, resource utilization), but it may also produce forecasts that look poor by conventional error standards. Another challenge is sample efficiency—RL techniques often require a vast amount of experience. If the time-series is slow-moving (like monthly sales data), the environment changes from month to month, so collecting enough episodes for reliable RL training can be challenging. Hybrid approaches that combine a forecasting model with a separate RL decision layer are often used in practice, balancing the benefits of each.