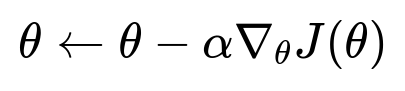ML Interview Q Series: Is it feasible to employ gradient-based optimization methods for cost functions that are not strictly convex?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Gradient descent is a fundamental optimization algorithm used to minimize a given objective or loss function J(theta). Even though it is often presented in the context of convex optimization, it is broadly applied to non-convex problems. Non-convex objective landscapes arise frequently in neural networks and complex machine learning models. Despite the presence of multiple local minima, saddle points, and flat regions, gradient descent and its variants are still practical and effective in many real-world tasks.

To understand why, consider the basic update rule of gradient descent. This rule reflects how we iteratively adjust the parameter vector theta based on the negative direction of the gradient of our loss function with respect to theta. Here is the core mathematical expression for the update:

Where theta is the parameter vector, alpha is the learning rate (a positive scalar hyperparameter controlling step size), and gradient J(theta) denotes the vector of partial derivatives of J with respect to the parameters. In a convex setting, following these gradients can guarantee a global optimum (under certain assumptions). In the non-convex case, global optimality is no longer guaranteed, but gradient descent can still converge to local minima or saddle points.

Below is a more elaborate exploration of the non-convex scenario:

When the cost function is non-convex, its surface can contain many local minima and saddle points. Consequently, gradient descent might settle in any of these local minima or in a broad flat region. In deep learning, extensive empirical studies show that many local minima in high-dimensional spaces can yield near-optimal performance on real-world datasets. Thus, although there's no theoretical guarantee for discovering the global optimum, gradient descent (and variants) is still a cornerstone of training large-scale models such as neural networks.

Hyperparameters like learning rate and advanced optimization techniques (such as Momentum, Adam, RMSProp, etc.) can help navigate complex non-convex landscapes by accelerating through narrow valleys and avoiding sharp local minima. Random initialization, along with multiple independent runs, can also help to find better local minima.

Another key concept is the presence of saddle points in high-dimensional settings. Some saddle points can be more “sticky” than local minima, and choosing a suitable learning rate schedule or using a small amount of noise (for instance, through stochastic gradient descent) often helps escape such points.

In practice, practitioners rely heavily on gradient descent and its variants for non-convex problems, especially in deep learning, because they work well in real-world scenarios, despite the theoretical obstacles like local minima or saddle points.

Code Example in Python

Below is a brief snippet illustrating a simple gradient descent applied to a non-convex function. This example uses a function with multiple local minima. While it is not guaranteed to reach the global optimum, it shows how we can implement the algorithm in a straightforward manner.

import numpy as np
import matplotlib.pyplot as plt

def non_convex_function(x):
    return np.sin(x) + 0.2 * x

def gradient_non_convex_function(x):
    # derivative of sin(x) + 0.2*x = cos(x) + 0.2
    return np.cos(x) + 0.2

# Hyperparameters
alpha = 0.01  # learning rate
iterations = 200
x_init = 5.0  # initial guess

x_vals = [x_init]
x = x_init

for i in range(iterations):
    grad = gradient_non_convex_function(x)
    x = x - alpha * grad
    x_vals.append(x)

# Plot results
x_plot = np.linspace(-10, 10, 400)
y_plot = [non_convex_function(xx) for xx in x_plot]

plt.plot(x_plot, y_plot, label='Non-Convex Function')
plt.plot(x_vals, [non_convex_function(xx) for xx in x_vals], 'ro-', label='Gradient Descent Path')
plt.legend()
plt.title("Gradient Descent on a Non-Convex Function")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.show()

Why Gradient Descent Still Works in Practice

Deep networks often have high-dimensional parameter spaces. Empirical evidence suggests that many local minima exhibit comparable performance, and certain regions in parameter space are wide “valleys” that generalize well. Tools like batch normalization, skip connections, and adaptive optimization methods further mitigate some of the issues caused by highly non-convex surfaces.

Multiple random restarts can also help discover different local minima, and ensemble methods can take advantage of the variety to improve predictions.

Potential Challenges and Pitfalls

Initializations can heavily influence where gradient descent converges in a non-convex landscape. A poor initialization can lead to suboptimal local minima. The learning rate must be chosen carefully; too large a rate can cause divergence, whereas too small a rate can prolong convergence or trap the algorithm in a poor local region. Vanishing and exploding gradients in deep neural networks also present significant optimization hurdles.

How to Mitigate Non-Convex Issues

Techniques like momentum-based gradient descent push updates in a direction aggregated from the current gradient and past gradients, helping to overcome narrow minima or saddle regions. Stochastic gradient descent adds noise that can occasionally help jump out of local traps. Advanced optimizers such as Adam or RMSProp adapt the learning rates for each parameter dimension separately, sometimes improving convergence for specific non-convex landscapes.

Regularization methods such as weight decay or dropout (in neural nets) can smooth the landscape or help the model avoid overfitting to spurious local minima. Curriculum learning or shaping the training process with simpler tasks first can aid optimization when faced with tricky landscapes.

Follow-Up Questions

How do multiple random restarts help in non-convex optimization?

Multiple random restarts can enable exploration of different regions in parameter space. Since each random initialization may converge to a distinct local minimum, evaluating performance across these minima might increase the likelihood of finding a more favorable optimum, even though it's not guaranteed to be global.

Are local minima in non-convex neural networks always problematic?

Not necessarily. In high-dimensional neural network landscapes, many local minima can be flat basins that yield similar performance. From a generalization perspective, wide and flat minima sometimes result in better performance on unseen data. This is because flat minima may be less sensitive to small perturbations in parameters, which can help the model generalize.

What about saddle points—why can they be worse than local minima?

Saddle points can slow or halt progress when the gradient in some directions is zero while being positive or negative in others. Algorithms like momentum-based optimizers and small injected noise from stochastic methods can help escape these saddle regions. In very high-dimensional spaces, saddle points are statistically more common than “bad” local minima.

Is second-order optimization useful for non-convex problems?

Second-order methods (like Newton’s method) involve the Hessian matrix of second derivatives. They can give more accurate search directions but become computationally expensive for large dimensional problems. Approximations of the Hessian (Quasi-Newton methods like L-BFGS) can be used in moderate-sized problems, but for very large-scale deep learning, these methods are often impractical. However, they can sometimes converge faster or escape problematic regions more reliably when they are feasible.

Would we ever know if we've reached the global minimum in a non-convex function?

In general, for highly non-convex problems, it is not trivial to guarantee the global minimum. We usually rely on empirical performance indicators such as validation loss and test accuracy to evaluate whether the solution is satisfactory, rather than proving global optimality.

Are there any theoretical results guaranteeing convergence for non-convex problems with gradient descent?

Some specialized classes of non-convex functions (e.g., functions satisfying certain smoothness and curvature conditions, or functions that are quasi-convex in certain regions) come with limited theoretical guarantees. For general neural network losses, there is no broad theoretical result that ensures global convergence. Research is ongoing to understand why, in practice, gradient-based optimization can still reliably find good solutions in high-dimensional spaces.

Below are additional follow-up questions

How does the geometry of high-dimensional non-convex loss surfaces influence the behavior of gradient descent?

Non-convex functions in high-dimensional parameter spaces (typical in deep neural networks) can exhibit complex geometric features, such as elongated valleys, steep cliffs, saddle plateaus, and numerous local minima. In very high dimensions, many local minima are often separated by narrow regions, making the overall loss landscape appear deceptively interconnected. This geometry means that while gradient descent can still converge to a local basin, the path taken can vary substantially depending on initialization, learning rate, or even data ordering in stochastic gradient methods.

A key pitfall is underestimating how “flatness” or “sharpness” in these regions impacts generalization. Wide, flat valleys often yield more robust models that are less sensitive to parameter perturbations, whereas sharp minima can overfit. Practitioners sometimes rely on small-batch training or added noise to help the algorithm wander into these flatter basins. However, this strategy can go awry if the noise is excessive, leading to difficulty converging or missing good minima altogether.

How do batch size choices in gradient descent affect convergence when dealing with non-convex loss landscapes?

The choice of batch size has a direct bearing on the stochasticity of the updates. A large batch size reduces the variance in the gradient estimates, which can help in more stable convergence but may also risk getting stuck in sharp local minima. A very small batch size adds more noise to gradient estimates, potentially helping to escape saddle points or poor local minima but at the cost of more erratic updates and longer training times.

Practical pitfalls arise if the batch size is too large for the available hardware memory, leading to out-of-memory errors. Conversely, if it is too small, training time may stretch significantly, and gradient estimates may become noisy enough to oscillate. Balancing these factors often requires empirical tuning and domain knowledge of the problem at hand.

Does the choice of activation function in deep networks affect the shape of the non-convex loss surface, and how do we mitigate potential pitfalls?

Activation functions like ReLU, sigmoid, or tanh lead to different geometric landscapes for the overall loss. For instance, sigmoid functions can cause regions of near-zero gradient (the saturated regime), creating long plateaus. ReLU functions can cause sharp transitions and “dead” neurons if the neuron output remains at zero for many inputs.

A potential pitfall is that certain activation functions, combined with poor weight initialization, may render the gradient nearly zero for a significant fraction of neurons. Techniques such as careful initialization, batch normalization, or skip connections can mitigate these issues by smoothing out the loss surface or ensuring gradients propagate more easily. Choosing the right activation function is often an empirical decision guided by prior experience and systematic experiments.

Can gradient descent get stuck in plateau regions or extremely flat minima, and how do we detect and handle such scenarios?

Plateaus in the loss surface occur when gradients are close to zero across large parameter regions. This can stall training for many iterations, giving the impression that the algorithm is stuck. Detecting plateaus can be done by monitoring the average gradient magnitude or loss improvement over intervals of updates. If these metrics remain nearly constant (or improve very slowly) for a large number of steps, the model may be in a plateau.

A practical remedy is to adjust the learning rate schedule. Sometimes reducing the learning rate too quickly can prolong staying in flat regions. Other times, slightly increasing the learning rate or adding more stochasticity (e.g., smaller batch sizes, higher momentum) can inject enough variability to escape these plateaus. Another approach is to adopt adaptive gradient methods (Adam or RMSProp) that dynamically rescale gradients, sometimes allowing them to “kick” the parameters out of flat zones.

What is the role of learning rate scheduling in non-convex optimization, and what pitfalls arise if the schedule is chosen improperly?

Learning rate schedules adjust the step size during training in order to speed up convergence when the surface is simpler to navigate and slow down updates when nearing a minimum. In non-convex landscapes, such schedules can help the model skirt around large curvature changes. Early in training, a larger rate can facilitate broad exploration and help escape undesirable regions. Later, a smaller rate refines the solution and avoids overshooting.

Pitfalls occur if the learning rate is decayed too aggressively, leaving the model stuck in a plateau or saddle region due to insufficient exploration. Alternatively, if the learning rate remains high, it can cause oscillations around minima or cause divergence. Implementing common schedules such as exponential decay, cosine annealing, or warm restarts must be accompanied by careful tuning and monitoring of validation performance.

How do skip (residual) connections in deep networks help with gradient descent on non-convex objectives?

Residual connections re-route information across layers, making it easier for gradients to flow backward through the network. This reshapes the effective loss surface, often making it smoother and reducing the likelihood of vanishing gradients. It also simplifies optimization by giving direct paths for parameter updates, effectively allowing a deeper network to behave more like a shallower one if the additional layers are not yet optimized.

A notable edge case arises if the residual path becomes a shortcut that the network overuses, effectively ignoring deeper layers. Monitoring layer outputs and ensuring that deeper layers actually learn non-trivial transformations is essential. Techniques like forcing certain transformations in deeper blocks or analyzing feature maps can confirm the residual connections are not simply bypassing learning.

What are the trade-offs in using a large versus small momentum term for non-convex optimization?

Momentum accelerates gradient descent by accumulating a velocity vector that represents past gradients. A larger momentum can help the optimization “plow through” small local basins or traverse flat plateaus more quickly. However, excessive momentum risks overshooting minima and causing unstable oscillations, especially in regions of sharp curvature.

Conversely, a smaller momentum provides more cautious updates, reducing oscillation but making it harder to move out of suboptimal minima or saddle points. The appropriate momentum balance often depends on the dataset, loss surface, and other hyperparameters. Tuning momentum, along with a suitable learning rate, is critical to avoid instabilities or slow convergence.

How does noise in data or labels impact gradient descent in a non-convex environment?

Real-world datasets often contain noisy inputs or mislabeled examples, which can distort the gradient signal. On the one hand, mild noise may aid exploration of the parameter space by injecting variability in gradients, helping the model escape bad local minima or saddle points. On the other hand, if the noise is too large or systematically biased, it can lead to convergence in poor regions of the loss surface or cause the model to overfit spurious patterns.

Detecting high noise may involve examining validation performance to see whether the training and validation losses diverge. Techniques like data cleaning, robust loss functions, or outlier filtering can reduce the impact of extreme label noise. In some cases, explicitly modeling the noise distribution (for example, using probabilistic approaches) can further stabilize learning.

In what scenarios might gradient descent fail for non-convex problems, and what are some mitigation strategies?

Failure can happen if the model encounters extreme curvature, pathological saddle regions, or vanishing/exploding gradients. In such cases, gradient descent might stall or produce numerically unstable updates. This is particularly problematic in deep or recurrent neural networks where gradients can vanish exponentially as they propagate backward.

Mitigation strategies include careful initialization (e.g., Xavier or Kaiming schemes), gradient clipping to limit exploding gradients, and architectural choices like gated recurrent units or residual connections that keep gradients flowing. Regular checks on gradients and losses can help detect potential failures. Additionally, employing a well-tuned adaptive optimizer (like Adam) can handle situations where different parameters require very different learning rates.

How can domain knowledge or constraints be incorporated into gradient descent for non-convex problems?

Incorporating domain knowledge can guide the optimizer toward physically meaningful or feasible regions. One approach is to constrain the parameter space, either explicitly (e.g., projecting parameters onto a valid set after each update) or implicitly (e.g., using penalty terms in the loss that impose domain-specific constraints). Another strategy is customizing the architecture to reflect known structure, which can reduce the effective dimensionality of the problem, making gradient descent more tractable.

Pitfalls include over-constraining the problem and removing useful flexibility in the model, resulting in underfitting. Conversely, domain constraints must be chosen carefully to avoid complicated, highly non-convex penalty terms that could worsen optimization. Striking the right balance between domain-specific constraints and model capacity often requires iterative experimentation and validation with real-world data.