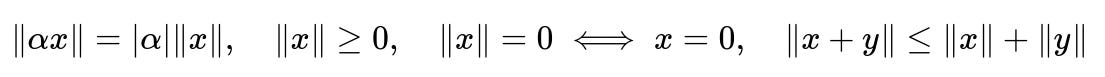ML Interview Q Series: Is it valid to treat the count of a vector’s nonzero entries as a norm? If not, provide the reasoning.
📚 Browse the full ML Interview series here.
Comprehensive Explanation
A function ‖x‖ that qualifies as a norm on a vector space must satisfy:
where x and y are vectors, and α is a scalar. The key property here is positive homogeneity (also called absolute scalability): when you multiply a vector x by a scalar α, the norm must multiply by the absolute value of α.
When we count the number of nonzero components in a vector (often referred to in the literature as the L0 “norm,” although it is not actually a true norm), it fails to meet this homogeneity requirement. Specifically, if we take a vector x with some nonzero entries and scale it by a nonzero scalar α, it does not change which entries are nonzero. Hence, the count remains exactly the same, rather than scaling proportionally to |α|. As an example, for any nonzero α, the number of nonzero elements of αx is identical to that of x, which violates the condition that ‖αx‖ = |α|‖x‖. Also, this count-based measure is not continuous and can fail the triangle inequality.
Despite these shortcomings as a norm, the count of nonzero components is sometimes used as a measure of sparsity in practical Machine Learning tasks. However, strictly from a mathematical standpoint, it does not fulfill the required axioms to be considered a norm.
Why This Fails the Norm Definition
Because the fundamental definition of a norm demands that scaling a vector must scale its norm by the same factor, any function that remains invariant under nonzero scaling (such as just counting how many components are nonzero) breaks that requirement. Therefore, while it is a useful notion for sparseness or complexity, it is not a valid norm.
Follow-Up Questions
What Are Some Practical Situations Where We Still Use the Count of Nonzero Elements?
In many feature selection or model complexity contexts, the number of nonzero parameters is used to measure how “sparse” a model is. Even though it is not a norm, many optimization procedures still try to minimize this quantity to achieve sparse representations or to perform feature elimination. For example, in compressed sensing and certain sparsity-driven learning algorithms, efforts are made to reduce the number of nonzero parameters.
Are There Approximate Ways to Handle This L0 Measure for Optimization?
Yes. Because the direct optimization of the count of nonzero elements is combinatorial and often infeasible for large-scale problems, continuous relaxations are commonly employed. A famous relaxation is the L1 norm, which promotes sparsity but is differentiable almost everywhere. Another approach involves iterative hard-thresholding or other approximate methods that attempt to zero out smaller components.
Does This Mean the L0 Pseudo-Norm Is Useless If It Is Not a True Norm?
Not at all. Although it is not a legitimate norm, it remains a powerful concept for tasks such as feature selection, sparse coding, and compression. It is a critical objective in many model selection criteria (e.g., controlling model complexity by limiting the count of parameters). The fact that it is not a norm only means it does not adhere to all the norm properties from pure mathematics, but it can still be integral to practical algorithms.
Why Does Continuity Matter in the Definition of a Norm?
Continuity ensures small changes in the vector produce correspondingly small changes in the norm. This property is crucial for stability and for the validity of the triangle inequality. The discrete jump from zero to nonzero in the count-based measure makes it discontinuous, which leads to complications in both analysis and optimization. Being continuous and obeying the triangle inequality also allows for many powerful theoretical results that facilitate analysis of convergence, error bounds, and geometry.
How Does the L1 Norm Compare to the Count of Nonzero Elements?
While the L1 norm is also known for encouraging sparsity, it does so in a softer manner by summing the absolute values of the components rather than counting nonzero entries. The L1 norm is a valid norm, as it satisfies the homogeneity, triangle inequality, and other norm properties. Minimizing the L1 norm can lead to many components being pushed toward zero, though not as sharply as with the direct count of nonzero entries.
Can One Construct a Modified Version of the L0 Measure That Satisfies the Norm Properties?
No variant of simply counting nonzero elements will satisfy the norm axioms, particularly the positive homogeneity property. While different generalized definitions and penalty functions exist, none of these that replicate the notion of “count of nonzero entries” can strictly satisfy the requirement ‖αx‖ = |α|‖x‖ for all α.
Practical Example of L0 Usage in a Learning Context
In certain regression tasks where the goal is to select a small subset of features, we may want to minimize the number of coefficients that are nonzero. The optimization objective might look like:
Sum of squared residuals + λ * (number of nonzero coefficients). While this is not a convex objective and not a norm-minimization problem, in practice, approximate or heuristic methods may be employed to search for a solution that has a small set of active features.
How to Justify Using the L0 “Norm” If It Is Not a True Norm?
The “L0 norm” label is historically a misnomer. In practice, it is easier to say “L0 measure” or “L0 pseudo-norm” to indicate it is not genuinely a norm but rather a count-based measure. People still use the term “L0 norm” for convenience, but one should keep in mind that it fails to meet the strict mathematical definition of a norm, and therefore the typical norm-based theorems do not directly apply.