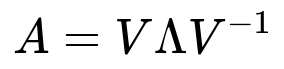ML Interview Q Series: Is the eigendecomposition of a real matrix always guaranteed to be unique? If not, how can we represent it?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
When we talk about the eigendecomposition of a matrix (especially a real matrix), we often ask whether there is a unique way to express that matrix in terms of its eigenvalues and eigenvectors. In general, uniqueness is not guaranteed. Multiple reasons contribute to this non-uniqueness:
If a matrix has repeated eigenvalues, the corresponding eigenspaces can be multi-dimensional, and hence there is freedom in choosing a basis for those eigenspaces.
Even if an eigenvalue is simple (not repeated), any scalar multiple of an eigenvector is still an eigenvector, so there is an inherent scaling ambiguity.
Real matrices that have complex conjugate eigenvalues do not admit a real diagonalization. Instead, they are sometimes represented using complex eigenvalues/eigenvectors or a real canonical form (such as a real Jordan or real Schur form).
One central way to denote the eigendecomposition (for a diagonalizable matrix) is often expressed as:
where:
A is the n x n matrix we want to decompose.
V is the matrix whose columns are the eigenvectors of A.
Λ (Lambda) is a diagonal matrix containing the eigenvalues of A on its diagonal.
V^{-1} is the inverse of V.
However, this decomposition is typically only directly valid if we allow complex numbers for any real matrix that is not guaranteed to be diagonalizable over the reals (for instance, if it has non-real eigenvalues). For real matrices with repeated or complex eigenvalues, we either switch to a complex representation or a canonical real form (such as a real Jordan normal form or a real Schur decomposition).
Why the Decomposition Is Not Unique
Scaling of Eigenvectors For any eigenvalue lambda with a non-zero eigenvector v, any constant c (not equal to zero) multiplied by v is still a valid eigenvector corresponding to the same lambda. This means if we take V and multiply one of its columns by a non-zero scalar, the product V * Λ remains valid (after an appropriate adjustment in V^{-1}), implying a non-uniqueness in the factorization.
Permutation of Eigenvalues and Eigenvectors We can rearrange the order of eigenvalues on the diagonal of Λ and correspondingly permute the columns of V. This does not alter the overall decomposition but yields a different arrangement.
Repeated Eigenvalues If the matrix has repeated eigenvalues, the eigenspace corresponding to that eigenvalue can have a dimension larger than 1. Any orthonormal (or linearly independent) basis spanning that eigenspace is valid, leading to infinitely many choices for the eigenvector basis in that subspace.
Complex Conjugate Pairs Real matrices often have complex eigenvalues that come in conjugate pairs if they are not symmetric (or not guaranteed to have real eigenvalues). Over the real field, you cannot diagonalize such a matrix, but you can still find a real Jordan normal form or a real Schur form. Over the complex field, you can diagonalize if the matrix is diagonalizable, but again, the decomposition is unique only up to the scaling and ordering considerations already mentioned.
How We Represent It When Uniqueness Fails
Jordan Normal Form (Complex Field) You can represent any diagonalizable matrix as VJV^{-1}, where J is a block diagonal matrix of Jordan blocks. This is done in the complex domain. If the matrix is not diagonalizable, some Jordan blocks will be larger than 1 x 1. Hence, even in the complex field, if we have repeated eigenvalues or Jordan blocks, there is more than one way to choose the generalized eigenvector basis.
Real Jordan or Real Schur Form If we prefer to keep representations within the real numbers, we often use the Schur decomposition: A = Q T Q^T (for real matrices, Q is orthonormal and T is block upper triangular). Each 2 x 2 block on the diagonal corresponds to a complex conjugate pair of eigenvalues. This representation is unique up to the order and choice of orthonormal basis in those 2 x 2 blocks.
Choosing Conventions for Uniqueness In practical applications, we often fix certain conventions (for example, requiring that each eigenvector has a norm of 1 and that the real part of the first component is positive) to remove some arbitrariness. Software libraries sometimes enforce these or similar rules when computing eigenvectors numerically. However, mathematically speaking, the core decomposition still remains non-unique.
Possible Follow-up Questions
How does a repeated eigenvalue affect the eigenvectors' space and decomposition?
Repeated eigenvalues indicate that the associated eigenspace can have dimension greater than 1. Suppose we have a repeated eigenvalue lambda repeated k times. The dimension of the corresponding eigenspace can vary from 1 to k. If it is exactly k, we say the eigenvalue has k linearly independent eigenvectors associated with it, which makes the matrix diagonalizable (at least with respect to that eigenvalue). Within that eigenspace, we can choose any orthonormal basis, leading to many equally valid decompositions.
Does having complex eigenvalues mean we cannot perform any real-valued decomposition?
Not exactly. If a real matrix has complex eigenvalues, you cannot diagonalize it with purely real eigenvectors because the eigenvectors will be complex. However, there are real-valued decompositions such as the real Schur form that arrange the matrix into block upper triangular form where each 2 x 2 block corresponds to a pair of complex conjugate eigenvalues. Another approach is the real Jordan form that uses blocks to accommodate those complex pairs. Both approaches stay in the real domain but do not yield a fully diagonal matrix.
What if the matrix is symmetric? Is the eigendecomposition unique then?
A real symmetric matrix (or Hermitian matrix, in the complex case) can be orthogonally (or unitarily) diagonalized. The eigenvectors can be chosen to be orthonormal, and all eigenvalues are real. Nevertheless, the decomposition is still not strictly unique because we can flip the sign of any eigenvector or permute eigenvectors for repeated eigenvalues. However, it is “unique” in the sense that the subspace spanned by the eigenvectors for each distinct eigenvalue is uniquely determined, and each eigenvalue is fixed. For repeated eigenvalues, there is still freedom in choosing a specific basis within that eigenspace.
Can numerical algorithms enforce a particular convention to achieve consistent results?
Yes, many linear algebra libraries implement specific normalization conventions. For instance:
They might choose the first non-zero element of an eigenvector to be positive.
They might order eigenvalues in ascending or descending order and keep eigenvectors in the corresponding order.
They might normalize eigenvectors to a unit norm.
Even with these conventions, strictly speaking, the decomposition has inherent flexibility. But these rules help produce reproducible outputs.
How is eigenvalue computation typically done in practice using Python libraries?
In Python, one commonly uses NumPy or libraries built on top of it (like SciPy). For example:
import numpy as np
A = np.array([[2, 1],
[1, 2]], dtype=float)
eigenvalues, eigenvectors = np.linalg.eig(A)
print("Eigenvalues:", eigenvalues)
print("Eigenvectors:\n", eigenvectors)
This yields an array of eigenvalues and eigenvectors. Internally, NumPy’s routines rely on well-known algorithms (e.g., the LAPACK library) for eigen decomposition, which might internally use the QR algorithm or the divide-and-conquer approach. Depending on floating-point round-off errors, slightly different representations can appear across machines or even runs, yet they represent the same fundamental eigendecomposition up to scaling and ordering of eigenvectors.
In summary, the eigendecomposition for a real matrix is not guaranteed to be unique due to factors like repeated eigenvalues, complex conjugate eigenvalues, and scaling/permutation freedom. We typically handle these ambiguities by adopting standard conventions or using real-valued canonical decompositions such as the real Jordan or real Schur forms.