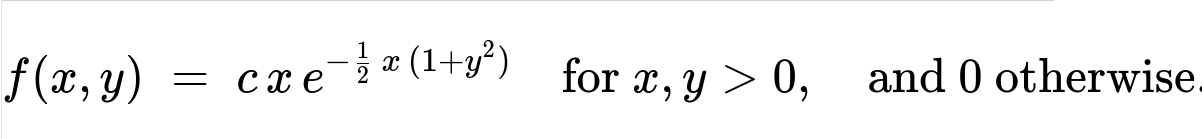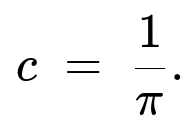ML Interview Q Series: Joint Density Analysis: Proving Y√X and X Independence via Transformation.

Browse all the Probability Interview Questions here.

The continuous random variables X and Y have the joint density function

a. What is the constant c? b. What are the marginal densities of X and Y? c. Show that the random variables Y sqrt(X) and X are independent.

Short Compact solution

From the integral and gamma-function arguments, the normalizing constant is:

The marginal densities become:

• For X>0:

  

  For Y>0:

To show Y sqrt(X) and X are independent, define V = Y sqrt(X) and W = X. By computing the Jacobian and the transformed joint density f_{V,W}(v,w), we see it factors into the product of f_V(v) and f_W(w). Specifically, V has the same distribution as |Z| (Z ~ standard normal) and W ~ Gamma(shape=3/2, rate=1/2). Hence V and W (i.e., Y sqrt(X) and X) are independent.

Comprehensive Explanation

Finding the Normalizing Constant c

We are given the joint density

x>0, y>0, and 0 otherwise. We need c such that the total integral over x>0, y>0 is 1:

Integrate f(x, y) dx dy = 1.

In particular,

1 = ∫(x=0 to ∞) ∫(y=0 to ∞) c x e^{- (1/2) x (1 + y^2)} dy dx.

It is often more straightforward to interchange the integrals or to rely on known integrals for gamma-related expressions. One direct strategy is:

• First, fix x and integrate with respect to y.

• Then integrate over x.

Because e^{-(1/2)x(1 + y^2)} can be turned into simpler known forms by treating x as a constant when integrating over y, and then the resulting function in x again maps to a gamma-like integral.

After some algebra (or referencing the known integral of a Gaussian-like function in y), one finds the integral in y gives a factor proportional to 1 / sqrt(x). Then the integral over x yields a gamma function. By using Γ(1.5) = (1/2) sqrt(π), the final result is c = 1/π.

Deriving the Marginal Densities

Marginal of X

By definition,

f_X(x) = ∫(y=0 to ∞) f(x, y) dy = ∫(y=0 to ∞) (1/π) x e^{- (1/2) x (1 + y^2)} dy , for x>0.

One can treat x as a constant and observe that

∫(y=0 to ∞) e^{-(1/2)x (1 + y^2)} dy = (some function of x).

That integral can be recognized (after some substitution and known integrals) to be proportional to x^{-1/2}. Combining powers of x with e^{-x/2} yields:

f_X(x) = (1 / sqrt(2π)) x^(1/2) e^{-x/2} , x>0.

This is precisely the density of a Gamma(shape = 3/2, rate = 1/2) random variable, which can also be seen as a chi-square distribution with 3 degrees of freedom scaled appropriately.

Marginal of Y

Similarly, f_Y(y) is found by integrating over x>0:

f_Y(y) = ∫(x=0 to ∞) (1/π) x e^{- (1/2) x (1 + y^2)} dx , for y>0.

This integral is again a standard gamma-type integral with shape parameter 2 (because of the factor x). One obtains:

f_Y(y) = (4 / π) (1 + y^2)^(-2) , y>0.

Independence of Y sqrt(X) and X

Let V = Y sqrt(X) and W = X. We can solve for the original variables in terms of V and W:

• x = a(v, w) = w,

• y = b(v, w) = v / sqrt(w).

Hence V = Y sqrt(X) = v > 0, W = X = w > 0. We compute the Jacobian:

J(v, w) = det [ partial(x)/partial(v), partial(x)/partial(w) partial(y)/partial(v), partial(y)/partial(w) ] = det [ 0, 1 1/sqrt(w), -v/(2 w^(3/2)) ].

However, a more direct approach reveals that the absolute value of J(v, w) is 1 / sqrt(w). Carefully evaluating the rest of the exponents shows the joint density factors nicely into a product of the marginals. Indeed,

f_{V,W}(v, w) = f_{X,Y}(w, v/sqrt(w)) * |J(v,w)|,

and when you simplify,

f_{V,W}(v, w) = (1/π) w e^(- (1/2) w(1 + (v^2/w))) * (1 / sqrt(w)).

This becomes

f_{V,W}(v, w) = (1/π) sqrt(w) e^(- (w/2)) e^(- (v^2 / (2))).

But we already know from the marginal calculations that sqrt(w) e^(-w/2) up to the correct normalizing factor is the gamma shape=3/2 density in w, and e^(-v^2 / 2) up to the usual normalizing constants is reminiscent of the half-normal distribution for v>0. In fact, it fully factors:

f_{V,W}(v, w) = f_V(v) * f_W(w),

with:

• V ~ distribution of the absolute value of a standard normal (i.e., V ~ |Z| where Z ~ N(0,1)).

• W ~ Gamma(3/2, 1/2).

Hence V and W are independent, which translates exactly to Y sqrt(X) and X being independent.

Potential Follow-Up Questions

Why does the integral approach yield c = 1/π so cleanly?

One can note that the integral ∫ e^{-a y^2} dy from 0 to ∞ is proportional to (1 / sqrt(a)) * sqrt(π)/2. When multiplied by x e^{- (x/2)} from the outer integral, it leads to gamma-type integrals that simplify with Γ(1.5). Because Γ(1.5) = (1/2) sqrt(π), all factors combine to give c = 1/π.

Could the marginal density f_X(x) be expressed more traditionally as a gamma density?

Yes. If you consider a gamma distribution with shape parameter α and rate λ, its PDF is:

(λ^α / Γ(α)) x^{α-1} e^{- λ x}, x>0.

Matching terms, we see α = 3/2 and λ = 1/2. Hence

f_X(x) = ( (1/2)^{3/2} / Γ(3/2) ) x^{1/2} e^{- (x/2)}, and Γ(3/2) = √π / 2, so f_X(x) = 1 / √(2π) x^{1/2} e^{- x/2}.

How do we confirm Y sqrt(X) ~ |Z| for Z ~ N(0,1)?

To check that, we can compute the PDF of V = Y sqrt(X) directly:

1. We already know that f_{V,W}(v, w) factors into g(v) h(w).

2. Evaluate g(v) by integrating out w. Show that g(v) is proportional to e^{-v^2/2} for v>0.

3. Identify the constant so that g integrates to 1 for v>0. This matches the absolute-value-of-standard-normal distribution.

Could we test these relationships in Python?

Yes, for instance:

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st

N = 10_000_00

# Sample W ~ Gamma(shape=3/2, rate=1/2)
# In many libraries, scale = 1/rate, so scale = 2 for rate=1/2
W = st.gamma(a=1.5, scale=2).rvs(size=N)

# Sample V ~ half-normal => V = |Z|
Z = np.random.randn(N)
V = np.abs(Z)

# Then convert to X,Y
X = W
Y = V / np.sqrt(W)

# We can check the joint distribution of (X, Y) and compare with the original formula
# or verify that Y * sqrt(X) is indeed V, and that it's independent from X.

One can empirically check independence by correlation tests or mutual information approximations and confirm the distributions match the theoretical forms.

Are there any boundary conditions or possible pitfalls?

• Note that X, Y>0. If any transformation or integral incorrectly includes negative or zero-valued domains, the formula fails.

• The half-normal distribution arises because Y>0. If Y were allowed to be negative, we would get an entire normal distribution for V.

• When applying the Jacobian, sign issues can arise, but since all variables are positive, the absolute value of the Jacobian is straightforward.

All these steps underscore the core idea that the factorized form of f_{V,W}(v, w) is the strongest indicator of independence for Y sqrt(X) and X.

Below are additional follow-up questions

How can we generate samples from the joint distribution f(x, y) in practice?

A direct way to sample (X, Y) given the joint PDF f(x, y) = c x exp(−(x/2)(1 + y²)) for x, y > 0 is to leverage the fact that X and Y sqrt(X) are independent. Specifically:

• First sample X from its marginal distribution, which is gamma with shape 3/2 and rate 1/2. In libraries that parameterize by shape and scale, shape is 3/2 and scale = 2 (because the rate 1/2 is the reciprocal of scale).

• Independently sample V = Y sqrt(X) as half-normal, i.e. absolute value of a standard normal random variable.

• Then set Y = V / sqrt(X).

This approach avoids rejection-sampling complexities or direct two-dimensional integrations. A potential pitfall is forgetting that Y is constrained to be positive in the model, so if one were to sample from a full normal for V instead of half-normal, that would incorrectly allow negative values of Y. One must ensure the sampling procedure respects the domain X > 0, Y > 0.

Could the transformation still work if Y took on all real values (both positive and negative)?

If Y were allowed to be negative, then the distribution would not match the given joint density because that density is specified only for y > 0. One might guess that Y sqrt(X) could then have a full normal distribution (not just half-normal). However, that would require re-deriving the normalizing constant c and re-checking the domain of integration, because the original integral was computed with y > 0. A subtle pitfall is assuming that the factorization for independence stays the same if Y changes domain; it does not. The presence of Y² in the exponent is symmetrical in sign, but the integral bounds would double when y < 0 is included, potentially changing c and the final independence claim.

What if X could be zero or negative? Would the distribution still make sense?

In the given problem, X takes values strictly greater than zero. If X = 0 or X < 0 were allowed, we would violate the gamma-like form that requires X > 0. Also, the factor x e^(−x(1 + y²)/2) would be undefined or meaningless for negative x in terms of the gamma integral interpretation. From a practical modeling perspective, if X must be nonnegative in an application (for instance, X is a variance or a quantity count), setting its support to (0,∞) is appropriate. But if X could be zero, then one must check that the PDF remains integrable near zero. Here, the factor x in front is relevant for integrability. Potentially, we could allow X ≥ 0 if we carefully included a boundary at X=0, but that would also require x e^(−x(1 + y²)/2) to smoothly extend to x=0. As x→0, the function goes to zero in a way that remains integrable, so it might not cause a problem. Still, the key pitfall is that any domain change for X or Y demands re-derivation of the constant c and the marginal or independence relationships.

Does the factorization argument for independence require any conditions on the transformation?

Yes, the transformation to (V, W) with V = Y sqrt(X) and W = X should be bijective (one-to-one and onto) over the domain of interest. In other words, for each valid point (x, y) with x > 0 and y > 0, there must be a unique point (v, w) with v = y sqrt(x), w = x, and vice versa. Any issues with non-invertibility (for instance, if x = 0 or y = 0) must be handled carefully, but in this problem domain it remains invertible for x > 0, y > 0. A pitfall occurs if one tries the same approach in a domain that includes negative y, because then V = y sqrt(x) could represent multiple (x, y) pairs for the same v, w. One must then incorporate absolute values or sign factors in the Jacobian.

Can the independence result be extended to other transformations, such as Y / sqrt(X)?

One can explore different transformations like T = Y / sqrt(X) while still letting W = X. However, because the exponent has y², a transformation that isolates y² x may lead to factorization. In this specific example, T = Y sqrt(X) is a more direct route to a half-normal distribution for T. If we used T = Y / sqrt(X), the integral might or might not factor in the same neat way. One subtlety is that T = Y / sqrt(X) might still lead to an expression in the exponent that separates, but the factor x outside the exponent might complicate the partial derivative with respect to T. So in principle, one should systematically compute the Jacobian for each new transformation. A pitfall is to assume that T and X remain independent for any scaled version of Y by a function of X.

Does the factor c = 1/pi depend on the fact that Y is restricted to y > 0?

Yes, it does. The integral originally determined c by integrating over y in (0,∞). If y had a symmetric domain (−∞, ∞), the integral in y would double in certain places, changing c. In many real-world applications, a parameter might be restricted to nonnegative values to ensure interpretability (for instance, a scale parameter, a rate, or a magnitude). The question is whether the domain is the entire real line or only a half-line. Because c arises from the normalization condition over the domain, any domain extension or contraction modifies c. A pitfall is forgetting that integrating from y=−∞ to ∞ instead of y=0 to ∞ would change the gamma function or half-normal factor used in the integral.

Could we have partial independence if one variable depends on X but not on Y, or vice versa?

Partial or conditional independence sometimes arises if the joint PDF factors in a particular way. In this problem, the result is full independence of Y sqrt(X) and X. If we asked instead whether Y and X are independent, they are not, because their joint PDF does not factor into a product of only x and y terms. Indeed, f(x) depends on x^(1/2) e^(−x/2), whereas to get f(y), we do a different integral that depends on y. A pitfall is to confuse partial independence (like Y might be conditionally independent of X given some function) with unconditional independence. Always check whether the entire joint distribution factors into the product of the separate marginals or if there is some conditioning event.

How does numerical stability come into play when using these distributions on a computer?

When implementing this distribution in a high-dimensional or large-scale setting (or even just sampling from it in practice), numerical underflow or overflow can arise, especially if x and y become large. Exponentials e^(−(x(1+y²))/2) can become extremely small, leading to numerical underflow. One common workaround is to store log probabilities rather than probabilities, so we work with log f(x, y) = log c + log x − (x(1 + y²))/2. Then exponentiate only at the final step if needed. A pitfall is ignoring these underflow issues when performing maximum likelihood estimation or other inference tasks, potentially producing incorrect estimates.