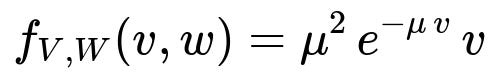ML Interview Q Series: Joint Density and Independence for Sum/Ratio of Exponentials via Variable Transformation

Browse all the Probability Interview Questions here.

11E-22. The random variables X and Y are independent and exponentially distributed with parameter μ. Let V = X + Y and

W = X / (X + Y). What is the joint density of V and W? Prove that V and W are independent.

Short Compact solution

Use the transformation (V, W) where V = X + Y and W = X / (X + Y). The inverse functions are X = v w and Y = v(1 − w). The absolute value of the Jacobian determinant is v. Because X and Y are i.i.d. Exp(μ), their joint density is μ e^(−μx) · μ e^(−μy) for x > 0, y > 0. Substituting x = v w and y = v(1 − w), we get

f_{V,W}(v, w) = μ² e^(−μv) · v for v > 0 and 0 < w < 1 and 0 otherwise.

Integrating out w from 0 to 1 gives f_V(v) = μ² v e^(−μv) for v > 0. Integrating out v from 0 to ∞ gives f_W(w) = 1 for 0 < w < 1. Therefore f_{V,W}(v, w) = f_V(v) f_W(w) for all v, w in the support, proving V and W are independent. In fact, V ∼ Erlang(2, μ) and W ∼ Uniform(0,1).

Comprehensive Explanation

Transformation Setup

We start with two random variables X and Y that are independent and each follows an exponential distribution with rate μ. This means X ≥ 0 and Y ≥ 0, and their joint density is:

f_{X,Y}(x, y) = μ e^(−μx) · μ e^(−μy) for x > 0, y > 0

We define two new variables:

• V = X + Y

• W = X / (X + Y)

We want the joint distribution of (V, W). To do so, we perform a change of variables from (X, Y) to (V, W).

Inverse Transformation

From V = X + Y and W = X / (X + Y), we solve for X and Y in terms of V and W:

X = v w Y = v (1 − w)

where v > 0 and w in (0,1). The domain of V is (0, ∞) and the domain of W is (0,1), because X and Y must remain nonnegative and W is the fraction X / (X + Y).

Jacobian Computation

We need the Jacobian determinant of the transformation (x, y) → (v, w). Specifically,

x = v w, y = v (1 − w)

so

∂(x, y)/∂(v, w) = | ∂x/∂v ∂x/∂w | | ∂y/∂v ∂y/∂w |

Substitute:

∂x/∂v = w, ∂x/∂w = v ∂y/∂v = 1 − w, ∂y/∂w = −v

So the determinant is:

(w)(−v) − (v)(1 − w) = −v w − v (1 − w) = −v [w + (1 − w)] = −v

The absolute value of this determinant is v.

Joint PDF of (V, W)

Using the standard change-of-variables formula for joint densities:

f_{V,W}(v, w) = f_{X,Y}(x, y) × |Jacobian|

We plug in x = v w and y = v (1 − w), and multiply by the Jacobian’s absolute value v:

• The original joint density f_{X,Y}(x, y) = μ e^(−μx) · μ e^(−μy) = μ² e^(−μ(v w)) e^(−μ(v(1 − w))) = μ² e^(−μv).

• The absolute value of the Jacobian is v.

Hence,

for v > 0 and 0 < w < 1, and 0 otherwise.

Marginal Densities and Independence

Marginal of V

To find f_V(v), we integrate out w from 0 to 1:

f_V(v) = ∫[w=0..1] f_{V,W}(v, w) dw = ∫[0..1] μ² v e^(−μv) dw

Since μ² v e^(−μv) does not depend on w over 0 < w < 1,

f_V(v) = μ² v e^(−μv) (1 − 0) = μ² v e^(−μv), v > 0

This is precisely the Erlang(2, μ) (or Gamma shape=2, rate=μ) distribution.

Marginal of W

To find f_W(w), we integrate out v from 0 to ∞:

f_W(w) = ∫[v=0..∞] μ² v e^(−μv) dv, for 0 < w < 1

The integral ∫[0..∞] μ² v e^(−μv) dv = 1 (which is a known result for the Erlang(2, μ) density). Hence,

f_W(w) = 1, 0 < w < 1

Thus W is Uniform(0,1).

Proof of Independence

If two random variables V and W have the property that their joint density factors into the product of their marginals, then V and W are independent. From above:

f_{V,W}(v, w) = μ² v e^(−μv) × 1 = f_V(v) f_W(w)

for all v > 0 and 0 < w < 1. Therefore, V and W are independent. Concretely, V follows an Erlang(2, μ) distribution, and W is Uniform(0,1).

Potential Follow-Up Questions

Why does X/(X + Y) end up Uniform(0,1)?

An important conceptual point is that if X and Y are i.i.d. exponential(μ) and we look at the ratio X / (X+Y), it can be shown—either by direct integration or by symmetry arguments—that this ratio is uniformly distributed on the interval (0,1). The direct change of variables approach we performed is the rigorous proof.

How can we interpret the Erlang(2, μ) distribution for V = X + Y?

Because X and Y are exponential(μ) and independent, the sum of two independent Exp(μ) random variables follows an Erlang distribution with shape 2 and rate μ. The PDF of Erlang(2, μ) is μ² v e^(−μv) for v > 0.

Could we have done this transformation if X and Y were not both exponential?

If X and Y have more general distributions, the distribution of X/(X+Y) need not be uniform, nor would the sum necessarily follow an Erlang distribution. This result critically depends on X and Y being i.i.d. exponential.

What happens if we consider a more general ratio, say (X / Y) or (Y / X)?

For exponential(μ) variables, the ratio X / Y follows a Pareto-like distribution (technically, an F(2,2) distribution), and is not uniform. The uniform distribution is a special property of X / (X+Y).

Implementation Detail in Python

Although this is more of a probabilistic concept, if you wanted to empirically verify that W is uniform and V is Erlang(2, μ), you could do a quick simulation:

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

mu = 2.0
n_samples = 10_000_00

X = np.random.exponential(scale=1/mu, size=n_samples)
Y = np.random.exponential(scale=1/mu, size=n_samples)

V = X + Y
W = X / (X + Y)

# Plot histograms to check empirically
sns.histplot(V, stat='density', bins=100, color='blue', label='V')
plt.title("Histogram of V = X + Y")
plt.show()

sns.histplot(W, stat='density', bins=50, color='red', label='W')
plt.title("Histogram of W = X/(X + Y)")
plt.show()

You would see that W appears uniform on (0,1), and V approximately matches the Erlang(2, μ) PDF.

Edge Cases and Practical Considerations

1. If either X = 0 or Y = 0 exactly (which has probability 0 in continuous distributions), the ratio W will be 0 or 1. But effectively, the distribution is supported on (0,1).

2. Numerical stability issues in practice: Directly computing X/(X+Y) for extremely large or extremely small values might require care if using floating-point arithmetic. Typically not an issue unless X+Y is near zero.

3. In more general contexts, the sum of exponentials with different rates can lead to a Hypoexponential distribution rather than Erlang.

This completes the proof and addresses typical follow-ups about the distribution of the sum and the ratio when dealing with i.i.d. Exponential(μ) random variables.

Below are additional follow-up questions

If X and Y had different rate parameters, would the ratio W still be uniform?

When X and Y are i.i.d. exponential(μ), W = X/(X+Y) is uniform(0,1) as a direct consequence of both the identical rate and the memoryless property. If X and Y have different rate parameters, say X ~ Exp(μ₁) and Y ~ Exp(μ₂) with μ₁ ≠ μ₂, then the fraction X/(X+Y) is no longer uniform(0,1). To see why, consider the underlying derivation: uniformity of W arises from the symmetry of the i.i.d. Exponential distribution. Once the rates differ, that symmetry breaks, and the ratio typically follows a Beta-like distribution that depends on the two rates.

A potential pitfall is forgetting that W’s distribution depends on the identical rates. When data exhibit significantly different scales for X and Y, it is incorrect to assume the ratio will be uniform.

What if the observed data for X or Y includes zeros or negative values?

Strictly speaking, an exponential distribution has support on (0,∞). If a real-world measurement process yields zeros or occasionally negative values (perhaps due to numerical issues, measurement errors, or some pre-processing artifact), the theoretical assumptions underlying the Exponential(μ) distribution are violated. In that case:

1. The transformation V = X + Y remains valid only for strictly positive X and Y.

2. The fraction W = X/(X+Y) becomes problematic if X+Y is 0 or if X is negative.

The subtlety arises if data “cluster” near zero in practice. Even though the probability of X+Y = 0 is theoretically zero, it might happen from sensor rounding or measurement cutoffs. This can cause high variance in W or produce undefined ratios. A robust data-cleaning step is needed to handle or discard those pathological cases.

How can we verify in practice that V and W are independent using sample data?

One practical approach is:

1. Generate or collect a sample of (X, Y).

2. Transform them to (V, W).

3. Estimate empirical marginal densities f_V and f_W, as well as the empirical joint density f_{V,W}.

4. Compare the product of the estimated marginals f_V(v) f_W(w) with the estimated joint f_{V,W}(v, w).

If V and W truly are independent, then f_{V,W} should approximately match f_V f_W at all points in the support. One can also use statistical tests such as a Chi-square test or a Kolmogorov-Smirnov-based test for two-dimensional distributions to assess independence.

A potential pitfall is using insufficient sample sizes. Independence might not be evident if the dataset is small or heavily discretized, leading to spurious correlations. Additionally, smoothing or binning choices in constructing empirical densities can artificially introduce or mask correlation.

What if we misapplied the Jacobian or ignored boundary constraints in the transformation?

A common error in change-of-variables problems is forgetting the absolute value of the Jacobian determinant, or worse, omitting the determinant entirely. Another error involves ignoring the domain restrictions: V must be positive, and W must lie in (0,1). If these constraints are not enforced, the derived PDF may incorrectly integrate to something other than 1 or assign positive density outside the actual feasible region.

Real-world significance: If people directly code a transformation in software and skip verifying the domain constraints, they might mistakenly produce nonsensical results (e.g., negative probabilities or densities that do not integrate properly).

Could a different function of X and Y also be independent from V?

In general, for i.i.d. exponential(μ) variables, V = X + Y has an Erlang(2,μ) distribution, and the specific fraction W = X/(X+Y) is uniform. If we consider a different function such as U = X² + Y or Z = min(X, Y), these new random variables might not remain independent from V.

For instance, consider U = X² + Y. Even though V = X + Y and X² + Y may each be well-defined, the pair (V, U) typically exhibits correlation because a larger X influences both X + Y and X² + Y. Hence, the independence we saw for (V, W) heavily relies on the ratio structure X/(X+Y), which symmetrically “normalizes” the sum.

How does the memoryless property of exponentials influence the result?

A key property of exponential(μ) is that P(X > t + s | X > s) = P(X > t). This memorylessness underpins many neat results involving sums, minima, or ratios of i.i.d. exponentials. In particular, the distribution of the first “arrival time” plus the second “arrival time” in a Poisson process leads to the Erlang distribution. The fraction X/(X+Y) being uniform can also be seen as a manifestation of how exponential waiting times “share” the total waiting period equally on average.

A subtlety is that if the random variables are not memoryless (e.g., gamma distributions with shape > 1, or lognormal distributions), the fraction X/(X+Y) does not simplify to a uniform distribution. In interviews, it’s easy to forget that memorylessness is a rare and special property in continuous distributions, belonging only to exponentials (and geometric for discrete).

Would the conclusion differ if X and Y were exponential but correlated?

One fundamental assumption in the derivation is that X and Y are independent exponentials. If there is correlation, the joint density would not factor into the product of marginals μ e^(−μx) · μ e^(−μy). Consequently, after the transformation to (V, W), the resulting joint density would not factor neatly as f_V(v) f_W(w). W would not, in general, remain uniform.

Real-world processes can have correlated waiting times: for instance, if some external factor simultaneously affects both X and Y. A pitfall is to incorrectly assume that “exponential-like data” always yields a uniform ratio. Without independence, many of these clean results break down, potentially misleading an analysis.

Does partial knowledge of (V, W) let us reconstruct X and Y exactly?

No. Knowing only V = X + Y and W = X/(X+Y) allows you to solve for X = V·W and Y = V·(1−W) in an idealized mathematical sense. That is a one-to-one transformation. However, in practice, partial knowledge might mean that we only observe V but do not observe W, or vice versa. If we only observe V, we cannot distinguish how much of V is due to X vs. Y. If we only observe W, we cannot infer the scale of X or Y, just the fraction. So to reconstruct the original pair (X, Y), we need both V and W (ideally, we need the entire set {V, W}).

A subtlety is measurement noise in each variable. If V is measured but W is approximated or noisy, back-calculating X and Y can compound errors. This is particularly troublesome in real data applications, for instance, if sensor precision is limited.