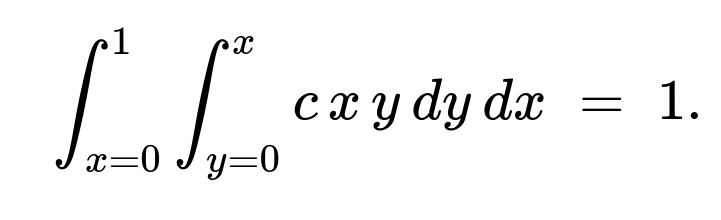ML Interview Q Series: Joint PDF Analysis: Normalization and Marginal Density Calculation via Integration.
Browse all the Probability Interview Questions here.
The joint density function of the continuous random variables X and Y is given by
and (f(x, y)=0) otherwise. What is the constant (c)? What are the marginal densities (f_X(x)) and (f_Y(y))?
Short Compact solution
From the normalization condition over the region (0<y<x<1), we get:
[ \huge \int_{x=0}^{1}!\int_{y=0}^{x} c,x,y ,dy,dx ;=; 1. ] Evaluating yields (c=8).
The marginal density of (X) is [ \huge f_X(x)=\int_{0}^{x} 8,x,y ,dy = 4x^{3} \quad \text{for }0<x<1,\quad 0\text{ otherwise}. ]
The marginal density of (Y) is [ \huge f_Y(y)=\int_{x=y}^{1} 8,x,y ,dx = 4,y,(1-y^{2}) \quad \text{for }0<y<1,\quad 0\text{ otherwise}. ]
Comprehensive Explanation
Finding the constant (c)
We are given a joint PDF (f(x,y) = c,x,y) defined on the triangular region (0 < y < x < 1). For a valid probability density function, we need
Let us break this down step by step:
The region of integration is (0 < y < x < 1). This means (y) goes from (0) up to (x), and (x) goes from (0) to (1).
First, integrate with respect to (y):
[
\huge \int_{y=0}^{x} c,x,y ,dy ;=; c,x \int_{0}^{x} y ,dy ;=; c,x ,\left[\tfrac{1}{2}y^{2}\right]_{0}^{x} ;=; c,x \cdot \tfrac{x^{2}}{2} ;=; \tfrac{c,x^{3}}{2}. ]
Next, integrate this result with respect to (x) from (0) to (1):
[
\huge \int_{0}^{1} \tfrac{c,x^{3}}{2}, dx ;=; \tfrac{c}{2} \int_{0}^{1} x^{3}, dx ;=; \tfrac{c}{2} \cdot \left[\tfrac{x^{4}}{4}\right]_{0}^{1} ;=; \tfrac{c}{2} \cdot \tfrac{1}{4} ;=; \tfrac{c}{8}. ]
We impose the condition that this must equal 1:
[
\huge \tfrac{c}{8} ;=; 1 \quad\Longrightarrow\quad c ;=; 8. ]
Hence, the constant (c=8).
Marginal density (f_X(x))
The marginal density (f_X(x)) is obtained by integrating the joint PDF (f(x,y)) over all possible (y) for a fixed (x). Since (0<y<x<1), for each (x) in ((0,1)) the possible values of (y) range from (0) to (x). Thus:
$$f_X(x) ;=; \int_{0}^{x} f(x,y),dy
;=; \int_{0}^{x} 8 ,x,y ,dy ;=; 8,x \int_{0}^{x} y ,dy.$$
Compute the inner integral:
[ \huge \int_{0}^{x} y,dy ;=; \tfrac{1}{2} x^{2}. ]
Multiplying by (8,x):
[
\huge 8,x \cdot \tfrac{1}{2} x^{2} ;=; 4,x^{3}. ]
Therefore,
[
\huge f_X(x) ;=; 4x^{3}\quad \text{for }0<x<1,\quad \text{and }f_X(x)=0\text{ otherwise.} ]
Marginal density (f_Y(y))
The marginal density (f_Y(y)) is obtained by integrating the joint PDF over all valid (x) for a fixed (y). Given (0<y<x<1), for each (y) in ((0,1)) the variable (x) goes from (y) to (1). Thus:
$$f_Y(y) ;=; \int_{x=y}^{1} f(x,y),dx
;=; \int_{y}^{1} 8,x,y ,dx ;=; 8,y \int_{y}^{1} x ,dx.$$
Compute the inner integral:
[ \huge \int_{y}^{1} x ,dx ;=; \tfrac{1}{2}\Bigl[1^{2} - y^{2}\Bigr] ;=; \tfrac{1 - y^{2}}{2}. ]
Thus:
[
\huge 8,y \cdot \tfrac{1-y^{2}}{2} ;=; 4,y,(1-y^{2}). ]
So,
[
\huge f_Y(y) ;=; 4,y,(1-y^{2}) \quad \text{for }0<y<1, \quad \text{and }f_Y(y)=0\text{ otherwise}. ]
Verifying the marginals integrate to 1
Check (f_X(x)):
[
\huge \int_{0}^{1} 4,x^{3}, dx ;=; 4 \left[\tfrac{x^{4}}{4}\right]_{0}^{1} ;=; 4 \cdot \tfrac{1}{4} ;=; 1. ]
Check (f_Y(y)):
[
\huge \int_{0}^{1} 4,y,(1-y^{2}) ,dy ;=; 4 \int_{0}^{1} \bigl(y - y^{3}\bigr), dy ;=; 4\left[\tfrac{1}{2}y^{2} - \tfrac{1}{4}y^{4}\right]_{0}^{1} ;=; 4\left(\tfrac{1}{2} - \tfrac{1}{4}\right) ;=; 4 \cdot \tfrac{1}{4} ;=; 1. ]
Both marginal densities integrate to 1, which is consistent with a valid probability density function.
Possible Follow-Up Questions
1) Why is the region of integration (0<y<x<1) and not (0<x<y<1)?
This region arises because the problem statement explicitly gives (f(x,y) = c,x,y) for (0 < y < x < 1). In other words, (x) must be strictly greater than (y) but both within ((0,1)). If the inequality were reversed ((x < y)), the joint PDF would be 0 in that region by definition.
2) Could (c) be negative?
No. For a probability density function to remain nonnegative everywhere in its support, the constant (c) must be positive (given that (x) and (y) are positive in that region). A negative (c) would make the density negative for positive (x) and (y), which is not permissible.
3) How can we visually interpret this integral?
You can think of the domain (0<y<x<1) as a triangular region in the unit square ((0,1)\times(0,1)). Graphically, you would be integrating the function (c,x,y) across that triangle where (y) is on the vertical axis and (x) is on the horizontal axis.
4) What if the roles of (x) and (y) were reversed?
If we swapped (x) and (y), we would be describing the region (0<x<y<1). The given PDF is zero there, so it would not affect the integral for the original question. However, if the problem had (f(x,y) = c,x,y) for (0<x<y<1), we would integrate accordingly over that different triangular region ((0<x<y<1)).
5) Could you provide a small Python snippet to numerically verify these integrals?
Below is an example using simple Monte Carlo approximation. This is just for verification, not for formal proof:
import numpy as np
def joint_pdf(x, y):
# c=8 for 0<y<x<1, else 0
return 8*x*y if (0<y<x<1) else 0
N = 10_000_000
samples = np.random.rand(N, 2)
# sort each sample pair so that x > y with 50% chance
# but let's explicitly keep only those where x>y
xs = samples[:,0]
ys = samples[:,1]
idx = xs>ys
xs = xs[idx]
ys = ys[idx]
# Estimate integral of joint_pdf over that region
vals = [joint_pdf(x, y) for x, y in zip(xs, ys)]
# Probability volume approximation
region_frac = len(vals)/N # fraction of points in 0<y<x<1 region
est = np.mean(vals)*region_frac
print("Estimated integral:", est)
If you run this code, the estimated integral will get close to 1, verifying that (c=8) is correct and that the joint PDF is normalized properly.
Below are additional follow-up questions
1) Are X and Y independent?
Answer
They are not independent. For two variables X and Y to be independent, we would require f(x, y) = f_X(x) * f_Y(y) for all x, y in their joint support. But from the computed marginals, we see:
f_X(x) = 4 x^3 for 0<x<1
f_Y(y) = 4 y (1 - y^2) for 0<y<1
If X and Y were independent, then f(x,y) would be (4 x^3)(4 y (1 - y^2)) = 16 x^3 y (1 - y^2). However, our actual joint density is 8 x y in the region 0<y<x<1, which is not equal to 16 x^3 y (1 - y^2). Thus, X and Y clearly do not satisfy the independence condition. Another intuitive explanation is that the domain restriction 0<y<x<1 couples X and Y, so knowing one constrains the possible values of the other.
2) What is the conditional PDF f(y | x) and how is it derived?
Answer
The conditional density f(y | x) is defined as f(x, y) / f_X(x) for valid x and y:
We have f(x, y) = 8 x y when 0<y<x<1 (and 0 otherwise).
We have f_X(x) = 4 x^3 when 0<x<1 (and 0 otherwise).
Hence, for a given x in (0,1), y ranges from 0 to x, so
f(y | x) = [8 x y] / [4 x^3] = 2 y / x^2, for 0<y<x<1.
Notice how the factor x>0 is critical because we divide by x^3 in the marginal. We also see that for a fixed x, f(y | x) is 0 outside the interval (0, x). To verify that this is a valid conditional PDF, integrate over y from 0 to x:
∫(y=0 to y=x) (2y / x^2) dy = (2 / x^2) * [y^2 / 2]_0^x = x^2 / x^2 = 1,
which confirms it is properly normalized for each x.
3) How do we compute E[X] and E[Y]?
Answer
To compute E[X], use the marginal density f_X(x) = 4 x^3 for 0<x<1:
E[X] = ∫(x=0 to x=1) x * 4 x^3 dx = 4 ∫(0 to 1) x^4 dx = 4 * (1/5) = 4/5.
To compute E[Y], use the marginal density f_Y(y) = 4 y (1 - y^2) for 0<y<1:
E[Y] = ∫(y=0 to y=1) y * 4 y (1 - y^2) dy = 4 ∫(0 to 1) y^2 (1 - y^2) dy = 4 ∫(0 to 1) (y^2 - y^4) dy = 4 [ (1/3) - (1/5) ] = 4 * (2/15) = 8/15.
Thus, E[X] = 0.8 and E[Y] ≈ 0.5333.
4) How would we compute Var(X) and Var(Y)?
Answer
Var(X) = E[X^2] - (E[X])^2. We already have E[X] = 4/5. We need E[X^2]:
E[X^2] = ∫(x=0 to x=1) x^2 * 4 x^3 dx = 4 ∫(0 to 1) x^5 dx = 4 * (1/6) = 2/3.
Hence,
Var(X) = 2/3 - (4/5)^2 = 2/3 - 16/25 = (50/75) - (48/75) = 2/75.
Similarly, for Y:
Var(Y) = E[Y^2] - (E[Y])^2. We have E[Y] = 8/15. Now compute E[Y^2]:
E[Y^2] = ∫(y=0 to y=1) (y^2 * 4 y (1 - y^2)) dy = 4 ∫(0 to 1) (y^3 - y^5) dy = 4 [ (1/4) - (1/6) ] = 4 * (1/12) = 1/3.
Then,
Var(Y) = 1/3 - (8/15)^2 = 1/3 - 64/225 = (75/225) - (64/225) = 11/225.
Hence Var(X) = 2/75 and Var(Y) = 11/225.
5) What is the covariance Cov(X, Y) and the correlation ρ(X, Y)?
Answer
Cov(X, Y) = E[XY] - E[X]E[Y].
First compute E[XY] using the joint PDF:
E[XY] = ∫(0 to 1) ∫(0 to x) (x y) * 8 x y dy dx = 8 ∫(x=0 to 1) ∫(y=0 to y=x) x^2 y^2 dy dx.
Inside integral over y:
∫(0 to x) y^2 dy = x^3 / 3.
So E[XY] = 8 ∫(0 to 1) x^2 ( x^3 / 3 ) dx = (8/3) ∫(0 to 1) x^5 dx = (8/3) * (1/6) = 8/18 = 4/9.
We already have E[X] = 4/5 and E[Y] = 8/15, so:
E[X] E[Y] = (4/5)*(8/15) = 32/75.
Thus,
Cov(X, Y) = 4/9 - 32/75 = 100/225 - 96/225 = 4/225.
Finally, the correlation coefficient ρ(X, Y) is:
ρ(X, Y) = Cov(X, Y) / ( √Var(X) * √Var(Y) ).
We have Var(X) = 2/75, Var(Y) = 11/225. Hence:
√Var(X) = √(2/75) = √2 / √75, and √Var(Y) = √(11/225) = √11 / 15.
So
ρ(X, Y) = (4/225) / [ (√2 / √75) * (√11 / 15 ) ] = (4/225) / [ (√2 * √11) / ( 15 * √75 ) ].
While we can leave it in this symbolic form, we can approximate numerically if desired. The key takeaway is that ρ(X, Y) > 0, indicating a positive correlation.
6) If we wanted to compute P(X + Y < 0.5), how would we proceed?
Answer
We need to integrate the joint PDF over the region { (x, y) : 0 < y < x < 1 } and x + y < 0.5. The constraints combine to:
0 < y < x
x + y < 0.5
x < 1 (though x < 0.5 is implied by x + y < 0.5 anyway)
Hence the feasible region is 0 < y < x < 0.5 - y. To set up the integral, we typically fix y first, then vary x:
For a given y, x ranges from x = something up to x = something. We see that 0 < y < x and x + y < 0.5 => x < 0.5 - y. So for each y, x goes from x=y up to x=0.5 - y.
y must be such that y < 0.5 - y => 2y < 0.5 => y < 0.25. So y goes from 0 to 0.25. Then x goes from y to 0.5 - y.
Therefore:
P(X + Y < 0.5) = ∫(y=0 to 0.25) ∫(x=y to 0.5 - y) 8 x y dx dy.
You would integrate with respect to x first and then y, being careful with the boundaries. This demonstrates how to handle more complex probability queries by carefully interpreting the geometric constraints.
7) How might we directly sample from this distribution without rejection sampling?
Answer
A straightforward way is to use the fact that Y ∈ (0, X) and the conditional PDF of Y given X is 2y / x^2 for 0<y<x. The steps would be:
Draw a random value of X from its marginal distribution f_X(x)=4x^3 for 0<x<1. You can do this by using the inverse CDF method:
Solve u = ∫(0 to x) 4t^3 dt = x^4 for x, giving x = u^(1/4). So if U is Uniform(0,1), define X = U^(1/4).
Conditioned on the sampled X, generate Y from the conditional PDF f(y|x)=2y/x^2 for 0<y<x. We again use the inverse transform:
For V ~ Uniform(0,1), solve V = ∫(0 to y) [2t / x^2] dt = (y^2 / x^2). Hence y = x√V.
By following these steps, each (X, Y) draw will be correctly distributed according to f(x, y) = 8 x y over the 0<y<x<1 region.
8) In practical applications, why might we prefer to check boundary conditions carefully for 0<y<x<1?
Answer
In real-world or simulation contexts, floating-point imprecision can cause issues if the boundary constraints are not handled carefully. For instance, if numeric approximations produce x and y values extremely close to 0 or 1, or if a tiny rounding error makes y slightly larger than x, the computed PDF might incorrectly be taken as nonzero outside the valid region. This can create small probability mass errors that accumulate in large-scale simulations.
One must ensure that the code respects 0<y<x<1 strictly.
If x or y is computed by transformations or iterative algorithms, round-off error near 1 might cause x or y to slightly exceed 1, making the PDF zero unexpectedly.
Implementing robust checks (such as min(max(...,0),1)) or specialized sampling routines ensures that all generated pairs (x,y) lie well within the valid domain.