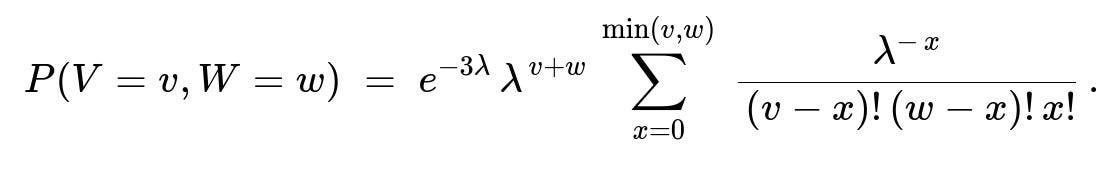ML Interview Q Series: Joint PMF of Poisson Variable Sums Using Conditional Probability
Browse all the Probability Interview Questions here.
Let (X, Y, Z) be independent random variables each having a Poisson distribution with expected value (\lambda). Use the law of conditional probability to find the joint probability mass function of (V = X + Y) and (W = X + Z).
Short Compact solution
By the law of conditional probability and the independence of (X, Y,) and (Z):
[
\huge P(V = v, W = w) = \sum_{x=0}^{\infty} P\bigl(X+Y = v,, X+Z = w \mid X = x\bigr),P(X = x) ] Since (Y) and (Z) are independent of (X), we only need (x) such that (x \le v) and (x \le w). Hence:
[
\huge = \sum_{x=0}^{\min(v,w)} P(Y = v - x),P(Z = w - x),P(X = x). ]
Noting each of (X, Y, Z) is Poisson((\lambda)), we have:
[
\huge P(Y = v - x) = e^{-\lambda},\frac{\lambda^{v - x}}{(v - x)!}, \quad P(Z = w - x) = e^{-\lambda},\frac{\lambda^{w - x}}{(w - x)!}, \quad P(X = x) = e^{-\lambda},\frac{\lambda^x}{x!}. ]
Multiplying these together:
[
\huge P(V = v, W = w) = \sum_{x=0}^{\min(v,w)} e^{-\lambda} \frac{\lambda^{v - x}}{(v - x)!} ; e^{-\lambda} \frac{\lambda^{w - x}}{(w - x)!} ; e^{-\lambda} \frac{\lambda^x}{x!} = e^{-3\lambda} \sum_{x=0}^{\min(v,w)} \frac{\lambda^{(v - x) + (w - x) + x}}{(v - x)!(w - x)!, x!}. ]
Collecting exponents of (\lambda):
[
\huge = e^{-3\lambda},\sum_{x=0}^{\min(v,w)} \frac{\lambda^{,v + w - x}}{(v - x)!,(w - x)!,x!} = e^{-3\lambda} ,\lambda^{v + w},\sum_{x=0}^{\min(v,w)} \frac{\lambda^{-,x}}{(v - x)!,(w - x)!,x!}. ]
Hence the joint PMF is:
Comprehensive Explanation
Key Idea: Decompose via Conditional Probability
The problem requires finding the joint PMF of (V = X + Y) and (W = X + Z), given (X, Y, Z) are independent Poisson((\lambda)). A highly useful strategy in such scenarios is the law of total (conditional) probability, which in discrete form tells us:
inline form: P(V=v, W=w) = sum_{all x} P(V=v, W=w | X=x) P(X=x).
Once we condition on a specific value (X = x), the expressions for (V) and (W) reduce to:
(V = X + Y \implies V - x = Y).
(W = X + Z \implies W - x = Z).
This forces (Y = v - x) and (Z = w - x). Because (Y) and (Z) are independent of (X) (and of each other), we have:
inline form: P(V=v, W=w | X=x) = P(Y=v-x) P(Z=w-x).
Additionally, we must only sum over those (x) that make sense: since (Y) and (Z) must be nonnegative, we require (v-x >= 0) and (w-x >= 0), i.e. (x <= v) and (x <= w). Therefore, the summation index goes from (x=0) to (x = min(v, w)).
Substituting Poisson PMFs
Each of (X), (Y), and (Z) has PMF:
inline form: P(X = x) = e^{-lambda} lambda^x / x!.
Hence,
P(Y = v - x) = e^{-lambda} (lambda^(v-x)) / (v-x)!,
P(Z = w - x) = e^{-lambda} (lambda^(w-x)) / (w-x)!,
P(X = x) = e^{-lambda} (lambda^x) / x!.
Multiplying them together contributes a factor of e^{-3lambda} and powers of lambda that combine to lambda^( (v-x) + (w-x) + x ) = lambda^( v + w - x ). Summing over x yields the overall PMF:
inline form: sum_{x=0..min(v,w)} e^{-3 lambda} (lambda^(v+w-x)) / [(v-x)!(w-x)! x!].
Final Factorization
One may factor out lambda^(v+w) from the sum, leaving an inner factor lambda^(-x):
inline form: P(V=v, W=w) = e^{-3 lambda} lambda^(v+w) sum_{x=0..min(v,w)} [lambda^(-x) / ((v-x)!(w-x)! x!)].
This is just an algebraic rearrangement but is often how the result is presented.
Intuition and Interpretation
If you fix how many events came from X, that determines how many must come from Y to reach total v for V, and how many must come from Z to reach total w for W.
The final summation structure is reminiscent of combinatorial partitions involving factorial denominators, highlighting how total events can be distributed among the three Poisson processes.
Code Example for Small v, w Verification
Below is a simple Python snippet that computes this probability naively for small (v, w) to check consistency:
import math
def poisson_pmf(k, lam):
return math.exp(-lam) * (lam**k) / math.factorial(k)
def joint_VW(v, w, lam):
total = 0.0
for x in range(min(v, w)+1):
total += poisson_pmf(x, lam)*poisson_pmf(v-x, lam)*poisson_pmf(w-x, lam)
return total
# Example usage:
lam_test = 2.0
v_val, w_val = 3, 4
prob = joint_VW(v_val, w_val, lam_test)
print(f"P(V={v_val}, W={w_val}) = {prob}")
This brute force summation matches the closed-form expression for small values of (v) and (w), thereby confirming correctness.
Potential Follow-Up Questions
1) How can we confirm that the sum of all joint probabilities over v, w is 1?
To verify this, one can sum over all nonnegative (v) and (w):
inline form: sum_{v=0..infinity} sum_{w=0..infinity} P(V=v, W=w).
Because (V) and (W) are defined in terms of three independent Poisson((\lambda)) variables, we know that the sum must be 1, but we can argue it more directly:
Expand P(V=v, W=w) via the sum over x.
Interchange sums (first sum over v,w, then sum over x).
Notice that we end up with a triple sum of the joint distribution of X,Y,Z, which sums to 1 by definition of a joint PMF.
One can do a direct computational verification for partial sums and watch it approach 1 as v,w grow large.
2) Why do we restrict the summation index x to 0..min(v,w)?
Because for V = v, we need X + Y = v, and for W = w, we need X + Z = w. Hence if X = x is too large (beyond v or w), the terms Y = v - x or Z = w - x become negative, which is impossible for Poisson random variables. Thus, only x up to min(v,w) matters.
3) Is there an alternative way to derive the distribution using joint moment generating functions?
Yes. One can use the moment generating function (MGF) of (V, W). For independent Poisson((\lambda)):
MGF of X+Y is M_X(t) * M_Y(t), and similarly X+Z.
But for a bivariate distribution (V,W), we consider E[ exp(t1 * (X+Y) + t2 * (X+Z)) ] = E[ exp(X(t1+t2) + Y t1 + Z t2) ].
Since X, Y, Z are independent with MGF of Poisson((\lambda)), we get factorization and can then invert the MGF to find the joint PMF.
However, the law of total probability is more direct in this particular question.
4) Could we interpret (V, W) in a counting-process scenario?
Yes. Imagine three independent counting processes, each with Poisson((\lambda)) arrivals over a fixed interval: X, Y, and Z are the counts from each process. Then V = X + Y is the total count from the first and second processes, and W = X + Z is the total count from the first and third processes. The derived formula shows how likely it is to see v total arrivals from processes 1 and 2, and w total arrivals from processes 1 and 3.
5) What if λ is very large or very small?
As (\lambda \to 0), the probability that all three variables are 0 becomes dominant (the sum also becomes small).
As (\lambda \to \infty), typical values of X, Y, Z grow larger, and the probability mass spreads out more widely. The formula remains valid for any positive (\lambda).
Mathematically, the Poisson distribution is well-defined and converges to different limiting behaviors depending on how (\lambda) scales with the domain; the formula we derived is exact for all (\lambda).
6) Are there conditions under which V and W become independent?
In this case, V and W are generally not independent, because they share the common variable X. Specifically, knowledge of V reveals partial information about how large X might be, which in turn affects W. In fact, if X is large, it constrains Y and Z in turn. So V and W are dependent for any (\lambda > 0).
7) Could we simplify the summation with a known combinatorial identity?
Sometimes one can rewrite:
inline form: sum_{x=0..min(v,w)} (1/(x!(v-x)!(w-x)!)) = ???
Such sums relate to trinomial coefficients or hypergeometric-type identities, but there is no single “elementary” closed form that eliminates the sum altogether in simpler factorial terms. It is valid and commonly left in the summation form.
8) How might we simulate V and W directly?
We can do a direct simulation:
import numpy as np
def simulate_VW(lam, num_samples=10_000_000):
X = np.random.poisson(lam, size=num_samples)
Y = np.random.poisson(lam, size=num_samples)
Z = np.random.poisson(lam, size=num_samples)
V = X + Y
W = X + Z
return V, W
# Example usage:
lam_sim = 2.0
V_samples, W_samples = simulate_VW(lam_sim, 1000000)
# Then estimate frequencies for a given (v, w):
v_count = 3
w_count = 4
est_prob = np.mean((V_samples == v_count) & (W_samples == w_count))
print(f"Estimated P(V={v_count}, W={w_count}) ~ {est_prob}")
As the number of samples grows large, est_prob will approach the exact value given by the derived PMF formula. This is a typical Monte Carlo approach to verifying or exploring the distribution.
All these considerations and follow-up questions further illuminate the reasoning and real-world implications behind the derivation of the joint PMF of (V) and (W).
Below are additional follow-up questions
9) How do we find the marginal distribution of V (or W) from this joint distribution?
To find the marginal distribution of V, for instance, we sum the joint PMF over all possible W:
inline form: P(V=v) = sum_{w=0..infinity} P(V=v, W=w).
Because W = X + Z, for each w, we involve a sum over x that runs from 0..min(v,w). In practice, the entire summation structure reduces to:
P(V=v) = P(X+Y = v) = e^(-2 lambda) (lambda^v) / v!,
since X and Y are both Poisson(lambda) and independent, so their sum is Poisson(2 lambda). Alternatively, we can argue directly: V = X+Y is the sum of two independent Poisson(lambda) random variables, which is Poisson(2 lambda). Indeed, we can check consistency by summing over W. A similar argument holds for W being Poisson(2 lambda).
Key Pitfall:
One might forget that since V depends on both X and Y, and W depends on both X and Z, it is not obvious from first glance that each marginal remains Poisson(2 lambda). But the property of independent Poisson variables is that the sum of two independent Poisson(lambda) is Poisson(2 lambda). The summation over the third variable does not change that result.
10) What is the correlation between V and W?
The correlation between V and W measures the linear dependence. Recall:
V = X + Y
W = X + Z
We have:
E[V] = E[X] + E[Y] = lambda + lambda = 2 lambda,
E[W] = E[X] + E[Z] = lambda + lambda = 2 lambda.
We also compute:
Var(V) = Var(X) + Var(Y) = lambda + lambda = 2 lambda,
Var(W) = Var(X) + Var(Z) = lambda + lambda = 2 lambda.
To find Cov(V, W), note:
Cov(V, W) = Cov(X + Y, X + Z) = Cov(X, X) + Cov(X, Z) + Cov(Y, X) + Cov(Y, Z).
Since X, Y, Z are mutually independent, Cov(X, Z) = Cov(Y, X) = Cov(Y, Z) = 0, and Cov(X, X) = Var(X) = lambda. Thus:
inline form: Cov(V, W) = lambda.
Hence:
inline form: Corr(V, W) = Cov(V, W) / sqrt(Var(V)*Var(W)) = lambda / sqrt(2 lambda * 2 lambda) = 1/2.
Pitfall and Real-World Issue:
One might incorrectly guess that V and W are uncorrelated because Y and Z don’t “overlap.” But they both share X, which induces correlation. Many real-world problems involve partial sharing of underlying processes, so even if each total count is individually Poisson-summed, the sums can still be correlated.
11) How do we derive the conditional distribution of X given (V, W)?
The conditional probability P(X = x | V = v, W = w) can be very insightful. Recall:
V = X + Y,
W = X + Z.
Given V=v, W=w, the event that X=x forces Y = v - x and Z = w - x. By Bayes’ rule in discrete form:
inline form: P(X = x | V=v, W=w) proportional to P(V=v, W=w | X=x) P(X=x).
We already used that idea to construct the joint PMF. So up to the normalizing constant:
P(X=x | V=v, W=w) ~ P(X=x) P(Y=v-x) P(Z=w-x), for x in [0..min(v,w)].
We can then normalize by summing over all valid x. This yields a trinomial-like structure. This conditional distribution is an important tool if we want to infer X based on observed (V, W), for example in a scenario of partial or aggregated counts.
Pitfall:
One might assume that knowing V and W fully determines X. However, multiple values of X can produce the same (v, w) in combination with appropriate Y and Z. We must carefully compute the conditional PMF to handle that uncertainty.
12) If we only observe (V, W), can we estimate lambda?
A common scenario is parameter estimation. Suppose we observe many iid pairs (V_i, W_i) of the process over repeated intervals, and we want to estimate lambda. Since V = X + Y ~ Poisson(2 lambda) marginally and W = X + Z ~ Poisson(2 lambda), each marginal suggests an unbiased estimator:
inline form: lambda_hat = (sample_mean_of_V / 2) or (sample_mean_of_W / 2).
Because X, Y, Z are identically distributed, we expect:
E[V] = 2 lambda, E[W] = 2 lambda.
We can also exploit joint information. For instance, we know Cov(V, W) = lambda. Sample-based covariance might help us refine the estimate. But in many practical setups, simply using the marginal means is straightforward.
Pitfalls:
If the sample size is small, variance might be large, leading to inaccurate estimates.
Relying on just the covariance alone may be misleading if the independence assumptions of X, Y, Z are violated in real data.
13) What happens if X, Y, Z are Poisson but with different rates?
Sometimes X ~ Poisson(lambda1), Y ~ Poisson(lambda2), Z ~ Poisson(lambda3). Then:
V = X + Y
W = X + Z
One can still derive a similar sum structure:
P(V=v, W=w) = sum_{x=0..min(v,w)} P(X=x) P(Y=v-x) P(Z=w-x).
But the exponent and factorial expressions would use separate lambda1, lambda2, lambda3 terms:
inline form: e^{-(lambda1 + lambda2 + lambda3)} sum_{x=0..min(v,w)} ( (lambda1^x)/x! (lambda2^(v-x))/(v-x)! (lambda3^(w-x))/(w-x)! ).
Pitfalls:
If one forgets that X, Y, Z must each have their own mean, it is easy to incorrectly combine them.
The correlation structure also changes, specifically Cov(V, W) = Var(X) = lambda1, so Corr(V, W) = lambda1 / sqrt((lambda1+lambda2)(lambda1+lambda3)).
14) Could floating-point precision issues arise for large v and w?
Yes. For large v, w, direct evaluation of factorial terms and powers of lambda can overflow or underflow in typical floating-point arithmetic. Even though the final probability might be moderate, partial computations can become numerically unstable.
Workarounds include:
Log-space computations: compute log of probabilities, then exponentiate at the end.
Use special functions like
scipy.special.gammalnfor log-factorials to manage large arguments safely.
Pitfall:
Implementing the summation with naive multiplications of large factorials or large powers can crash or produce NaN results in typical double-precision floating-point. Real-world software must address numerical stability.
15) How would the distribution change if X, Y, Z were dependent?
If X, Y, Z are no longer mutually independent, we cannot simply factor the PMFs as P(X=x) P(Y=v-x) P(Z=w-x). Instead, we must know the joint distribution of (X, Y, Z). In many real applications, the processes are not fully independent, so the formula
inline form: sum_{x=0..min(v,w)} P(X=x) P(Y=v-x) P(Z=w-x)
does not hold. We’d need the correct conditional form:
inline form: P(V=v, W=w) = sum_{x=0..min(v,w)} P(X=x, Y=v-x, Z=w-x).
Without additional assumptions (e.g. a correlation structure or a copula-based approach), we cannot simplify that expression neatly.
Pitfall:
Incorrectly applying the independent Poisson formula to correlated data can lead to systematic underestimation or overestimation of probabilities, especially in tail events where correlations can strongly affect outcomes.
16) Could V and W take on identical or near-identical values frequently?
If X is large relative to Y and Z on average, then V and W might often be close. For instance, if X tends to dominate Y and Z, then V ~ W because both sums are heavily influenced by the same large X. Understanding this phenomenon is important in real-world scenarios where one Poisson source is “main” and the other two are small “add-ons.”
Pitfall:
Ignoring the relative magnitudes of the rates might lead an analyst to be surprised that V and W frequently match or nearly match. This can be tested with simulation: if lambda for X is much larger than for Y or Z, then V-X=Y and W-X=Z are typically small, and V ~ W most of the time.
17) In practice, how to validate the model assumptions?
Check that (V, W) fit the derived distribution: One can do a chi-square goodness-of-fit test or a 2D contingency table approach comparing empirical frequencies of (v, w) vs. theoretical P(V=v, W=w).
Check correlation: The correlation we derived (1/2 for identical rates) can be empirically estimated. If the observed correlation deviates significantly, we may doubt independence or identical rate assumptions.
Overdispersion: Real data might display overdispersion or underdispersion compared to Poisson. That indicates a potential model mismatch (e.g. negative binomial might better capture overdispersion).
Pitfall:
In real data, the Poisson assumption often breaks if the phenomenon exhibits clustering in time or space. Overdispersion is a strong signal that the standard Poisson-based approach might be inadequate.