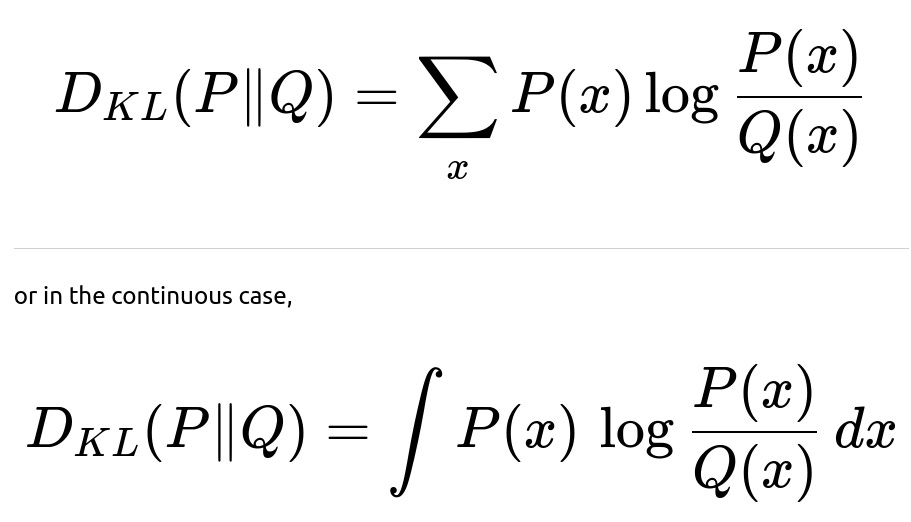ML Interview Q Series: Kullback–Leibler Divergence: Measuring Distribution Differences in Machine Learning.
📚 Browse the full ML Interview series here.
KL Divergence: What is Kullback–Leibler (KL) divergence and how is it used in machine learning? Explain what it means for KL divergence to be 0, and give an example of an application (such as in model training or measuring distribution shift) where you would minimize a KL divergence.
Understanding KL Divergence
Kullback–Leibler (KL) divergence is a statistical measure of how one probability distribution diverges from a second, reference probability distribution. In simpler terms, it quantifies the “distance” or dissimilarity between two distributions, although it is not a true distance metric (because it is not symmetric and does not satisfy the triangle inequality).
The KL divergence from a probability distribution P to another probability distribution Q, defined over the same probability space, is often expressed as:
In words, KL divergence measures how “inefficient” it is to assume that samples come from Q when they actually come from P. The larger the divergence, the more Q diverges from faithfully modeling P.
Why KL Divergence is Useful in Machine Learning
KL divergence appears in many parts of machine learning, particularly because it helps measure how different one distribution of data or model predictions is from another. It is used in tasks such as:
Training generative models (e.g., Variational Autoencoders): The objective function can include a KL term to ensure that a learned approximate distribution is close to a desired prior distribution.
Model regularization and fitting: Minimizing KL divergence is equivalent to maximizing the likelihood of the data under a probabilistic model in many scenarios.
Distribution shift detection: By comparing the distribution of new, incoming data to a known baseline distribution, practitioners can detect if there has been a shift or drift that makes the old model or old assumptions inaccurate.
Meaning of KL Divergence Being 0
KL divergence is always non-negative. It is 0 if and only if the two distributions are exactly the same for almost every point in the space (in other words, P and Q match perfectly everywhere). In discrete terms, for every outcome x in the support, P(x) equals Q(x). This property follows from Gibbs’ inequality.
Example of Application: Minimizing KL Divergence
A classic example is in model training, where we often optimize the cross-entropy loss between the data’s true distribution P and the model’s predicted distribution Q. The cross-entropy loss can be decomposed into the entropy of P plus the KL divergence between P and Q. Because the entropy of P is constant with respect to Q, minimizing cross-entropy is effectively minimizing the KL divergence between P and Q, thus making the model’s predicted distribution Q close to the true data distribution P.
Another application is in measuring distribution shift. If you collect baseline data (distribution P) for a production environment and then later observe new data (distribution Q), you can compute KL divergence to see if the new data significantly diverges from P. If the KL divergence is high, it indicates the new data differs substantially from the baseline.
Use in Practice
In practical machine learning frameworks:
import torch
import torch.nn.functional as F
# p and q are probabilities (after softmax) for discrete classes
# p is the target distribution, q is the predicted distribution
def kl_divergence(p, q):
# Typically we ensure p and q are probabilities that sum to 1
# We can compute KL Divergence as:
return torch.sum(p * torch.log(p / q), dim=-1)
Minimizing this quantity over your dataset encourages q to match p more closely, thereby reducing divergence.
What if P Contains Zeros Where Q is Non-Zero?
In practice, KL divergence can become numerically unstable if P contains zeros or Q is zero at certain points. This is one reason why many modern frameworks prefer stable approximations. Practitioners might add small epsilons to probabilities to avoid undefined or infinite log values.
Why is KL Divergence Asymmetric?
KL divergence measures how well Q explains P’s samples, rather than how well P explains Q’s samples. If you swap P and Q in the expression, you get a different quantity. This asymmetry matters in some scenarios (like model training) where you have a specific direction in mind: “How well does the model’s distribution approximate the data distribution?”
How is KL Divergence Used in Variational Inference?
In variational autoencoders and other variational inference methods, we typically have a latent variable model. We approximate an intractable posterior distribution of latent variables with a variational distribution. The training objective often has a term that penalizes the KL divergence between the variational distribution and a known prior. Minimizing this KL term helps keep the variational distribution from deviating too far from the prior, promoting generalization and stable training.
Potential Pitfalls When Using KL Divergence
One subtle pitfall is that KL divergence heavily penalizes places where Q assigns very low probability but P has relatively high probability (because the log term becomes large and positive). If your model distribution Q never assigns enough probability mass to important regions of P, the divergence can blow up. Additionally, KL divergence may not capture certain aspects of distribution mismatch that are relevant if you need a symmetric measure (e.g., if you want to see how far each distribution is from the other in both directions). In those cases, people sometimes consider alternative measures like Jensen–Shannon divergence or other distance metrics.
How Can You Tell If Your KL Divergence is Too High?
A large KL divergence means your predicted distribution Q is quite far from the true distribution P. In practical tasks like classification, if your model often places substantial probability on the wrong classes, the KL divergence to the correct distribution (which places all the mass on the correct class in many training schemes) will become high. Monitoring KL divergence during training can help diagnose whether your model is underfitting (very high KL) or if it’s converging appropriately (KL trending down).
Example to Illustrate Minimizing KL Divergence in Training
Suppose you have a dataset of images labeled with classes 1 through 10, and you train a neural network to predict these classes. If you treat each label in a one-hot manner, P is the distribution with a 1 for the correct class and 0 for all others. Meanwhile, Q is your model’s softmax output for that image. Minimizing cross-entropy (which is equivalent to minimizing KL divergence plus a constant term) encourages Q to place the majority of its probability on the correct label. When your model perfectly classifies all images, Q for each image is effectively the same as P (the correct one-hot label), thus making KL divergence 0.
Follow-up Question: Could KL Divergence Ever be Negative?
KL divergence is always non-negative due to Gibbs’ inequality and the properties of logarithms. It is 0 exactly when P and Q coincide almost everywhere. It cannot go below 0. In practice, you might see floating-point artifacts if your numerical computations are unstable (like negative values approaching zero), but theoretically it is never negative.
Follow-up Question: How to Handle Cases Where P is Continuous and Q is Discrete?
If P is a continuous distribution and Q is a discrete one, or vice versa, the KL divergence is not straightforward to define unless you map them both to a consistent probability space. One might need to discretize the continuous distribution or approximate one distribution with a continuous function. Typically, you ensure both P and Q are of the same form—both discrete or both continuous—and defined on the same set or space.
Follow-up Question: Why Might One Use Jensen–Shannon Divergence Instead?
The Jensen–Shannon (JS) divergence is a symmetrized and smoothed version of KL divergence. It is defined as:
where M is the midpoint distribution (the average of P and Q). Unlike KL divergence, JS divergence is always finite and symmetric. It also has a bounded range between 0 and 1 (for distributions expressed in log base 2). Practitioners prefer JS divergence in some generative modeling tasks because it can provide smoother gradients and avoid excessively large penalty regions. However, KL divergence remains standard in many applications due to its direct interpretation and relationship with maximum likelihood training.
Follow-up Question: Why is Minimizing Cross-Entropy the Same as Minimizing KL Divergence?
The cross-entropy between P and Q is:
where (H(P)) is the entropy of the distribution P (a constant with respect to Q). Because (H(P)) does not depend on Q, minimizing cross-entropy with respect to Q is equivalent to minimizing the KL divergence. This fact underlies many classification training objectives: the standard cross-entropy loss can be viewed as matching the distribution of your network outputs to the distribution given by your labels.
Follow-up Question: In What Situations Might KL Divergence Not Be the Best Metric?
KL divergence might not be suitable if you need a symmetric measure of dissimilarity. For instance, in cases where you need a “distance” that does not overly penalize small differences on the tail side of P, a different measure might be more appropriate. Also, if both distributions have support in different regions, KL can diverge to infinity (if Q is zero in regions where P is non-zero). Practitioners sometimes use the Rényi divergence, Wasserstein distance, or Jensen–Shannon divergence, depending on the specific domain requirements and stability considerations.
Below are additional follow-up questions
How does KL Divergence relate to offline Reinforcement Learning (RL) when the data distribution for training is fixed, and the policy being learned might deviate from that distribution?
In offline RL (sometimes called batch RL), the agent receives a fixed dataset of transitions (state, action, next state, reward) to learn a policy. A major challenge is distribution mismatch: if the learned policy picks actions that are rarely (or never) in the offline dataset, the value function estimates may become poor or extrapolation error can grow significantly. KL divergence can be relevant here:
Reasoning: One approach to address distribution mismatch is to constrain the learned policy to remain close to the behavior policy that generated the dataset. This can be done by penalizing a KL divergence term between the policy you want to learn (call it ( \pi_\theta )) and the behavior policy ( \mu ). If you excessively deviate, then you might place mass on actions that the dataset does not sufficiently cover, leading to poorly estimated Q-values or transitions. By minimizing a KL penalty, you force the new policy to stay within a region where you have enough data coverage.
Pitfalls:
Overly strict KL constraints could limit the policy from exploring better actions that were not well-represented in the dataset.
Conversely, if the KL constraint is too loose, the policy might place mass on actions with little to no coverage, leading to high variance or biased value estimates.
Computing KL in high-dimensional continuous action spaces might require approximation techniques or reparameterizations. Poor approximation or ignoring small tails in continuous distributions can lead to numerical instability or suboptimal solutions.
In the presence of label noise, how does minimizing KL Divergence behave, and what are typical pitfalls?
Label noise means that the “true” distribution over labels ( P ) may be corrupted by random flips or distortions. When you minimize KL divergence (or equivalently cross-entropy) between your model predictions ( Q ) and these noisy labels, certain complexities arise:
Reasoning:
If label noise is moderate, the model might learn to “average out” the noise. In a multi-class setting, you might see predicted probability distributions become less peaked because it tries to hedge against incorrect labels.
With severe noise, direct minimization can degrade model performance or lead to overfitting if the model tries to perfectly fit random or contradictory labels.
Pitfalls:
Memorization: Deep models can eventually memorize noisy labels, which inflates training accuracy but yields poor generalization.
Confidence Calibration: If the model tries to “correctly” fit contradictory examples, the predicted distribution can become miscalibrated, harming downstream tasks like uncertainty estimation.
Remedy: Techniques like label smoothing or filtering out probable mislabeled samples can help. Sometimes, reweighting samples or using a robust loss function (e.g., symmetric KL divergence or other robust divergences) might improve resilience to noise.
In multi-class classification with extremely imbalanced data, how should one interpret or adjust KL Divergence minimization?
When classes are heavily imbalanced, the empirical distribution ( P ) might put a large portion of the mass on a few dominant classes, and relatively little mass on minority classes:
Reasoning:
Minimizing KL divergence (or cross-entropy) in an imbalanced context often leads the model to be highly accurate on dominant classes but potentially ignore minority classes, because the average penalty from misclassifying minority samples can be overshadowed by the abundant majority examples.
KL divergence does not inherently “balance” the classes unless you explicitly reweight or reshape the distribution.
Pitfalls:
Overfitting to Majority Classes: A naive minimization of KL might lead to trivial solutions where the model predicts mostly the majority class, yielding poor recall on minority classes.
Metric Mismatch: Imbalanced classification problems often require metrics like F1-score, balanced accuracy, or AUC. A model that simply optimizes KL divergence might not maximize these alternative metrics.
Solutions: Strategies like upsampling minority data, downsampling majority data, or adjusting the label distribution (for instance, cost-sensitive weighting in cross-entropy) can mitigate imbalance issues.
Can KL Divergence be used to detect outliers or anomalies, and what are the subtle issues involved?
KL divergence can help in anomaly/outlier detection if you have a baseline “normal” distribution ( P ) and you observe new data distribution ( Q ). By checking if ( D_{KL}(Q | P) ) or ( D_{KL}(P | Q) ) is large, you might infer anomalies:
Reasoning:
If data is typical of the baseline, you expect a low divergence. If new data has significantly different patterns or feature distributions, the divergence grows.
This approach is commonly used in tasks like intrusion detection or quality monitoring in manufacturing.
Pitfalls:
High-Dimensional Data: Estimating distributions in high dimensions is difficult. Approximating KL divergence can become unreliable if not done with care (e.g., using kernel density estimates or neural-based density estimations might be sensitive to hyperparameters).
Support Mismatch: If the new data distribution has support where the baseline distribution has zero density, the KL can be infinite, which may or may not be helpful depending on the application.
Practical Stability: Numerical computations of logs and small probabilities can lead to instability, requiring smoothing or thresholding strategies.
What is the difference between forward KL ( D_{KL}(P | Q) ) and reverse KL ( D_{KL}(Q | P) ), and how does that impact generative modeling?
The KL divergence is asymmetric, so choosing which distribution is “first” in the KL expression matters greatly:
Reasoning:
Forward KL ( D_{KL}(P | Q) ) measures how well ( Q ) covers all the regions where ( P ) has probability mass. If ( Q ) places very little probability in areas where ( P ) is large, the term ( \log \frac{P(x)}{Q(x)} ) becomes large, heavily penalizing that mismatch. Forward KL tries to cover all of ( P )’s support to avoid infinite divergence.
Reverse KL ( D_{KL}(Q | P) ) focuses on how concentrated ( P ) is relative to ( Q ). If ( Q ) puts a lot of probability where ( P ) is negligible, the penalty is large. Reverse KL can lead to “mode-seeking” behavior, because it tries to align its probability mass with the biggest modes of ( P ).
Pitfalls:
In generative modeling, using forward KL (like maximum likelihood estimation typically does) can lead to “coverage” solutions that try to spread out probability to cover all modes of ( P ), sometimes producing overly “blurry” samples in image generation.
Using reverse KL can lead to mode collapse, where the model picks a subset of modes but fits them tightly. This might yield sharper samples but fail to represent all of the data distribution’s variety.
Many modern methods (e.g., some GAN variants) effectively minimize symmetrical or other divergences (like Jensen–Shannon) to balance coverage and mode-seeking behaviors.
How does KL Divergence come into play in Bayesian neural networks that utilize approximate posteriors, such as with dropout or variational methods?
In Bayesian neural networks, especially with variational inference, we approximate the true posterior over weights ( p(w \mid \text{data}) ) with a tractable distribution ( q_\theta(w) ). The variational objective typically has a KL term:
Reasoning:
We want ( q_\theta(w) ) to be close to ( p(w \mid \text{data}) ), but the exact posterior is often intractable. Instead, we minimize the KL divergence ( D_{KL}(q_\theta(w) | p(w \mid \text{data})) ) or some rearranged form in the evidence lower bound (ELBO).
This encourages the approximate posterior to not stray too far from the prior or from the shape of the true posterior derived from the data.
Pitfalls:
Mode-seeking vs. Mode-covering: Because the KL is typically ( D_{KL}(q_\theta | p) ) (reverse KL) in a standard variational setup, the approximate distribution can under-cover some posterior modes. This might lead to underestimation of posterior uncertainty.
Over-regularization: If the KL term is weighted too strongly relative to the data likelihood term, the approximation might stay very close to the prior and thus ignore important data signals.
Empirical Tuning: In practice, one often has a “beta-VAE” style approach or similar weighting on the KL term to strike a balance between data fit and prior closeness.
In real-world continuous distribution problems, what if you only have discrete samples for one distribution, while the other distribution is analytically known?
It’s common to have a parametric or known distribution ( Q(x) ) and only samples from ( P(x) ). Estimating ( D_{KL}(P | Q) ) becomes tricky:
Reasoning:
You might attempt a Monte Carlo approximation: for each sample ( x_i \sim P ), approximate ( \log \frac{P(x_i)}{Q(x_i)} ). But ( P(x_i) ) might be unknown in closed form, only implicitly known via samples. You then need to use a density estimation technique for ( P ) (e.g., kernel density or a neural density estimator).
Alternatively, you might approximate ( P \log \frac{1}{Q} ) plus other terms if you can do density ratio estimation or other advanced techniques.
Pitfalls:
Density Estimation Error: Attempting to estimate ( P(x) ) in high dimensions can be fraught with overfitting or underfitting, leading to large variance or bias in the KL estimate.
Choice of Binning or Kernel: If using discrete bins or kernel-based methods, the results can be highly sensitive to the bandwidth or bin size.
Support Issues: If your discrete samples do not cover the space well, you might severely underestimate or overestimate the divergence.
Could KL Divergence be used in ensemble methods for comparing the predictions of multiple models, and how might one interpret or mitigate discrepancies?
When building ensembles, you often have multiple models that produce distributions ( Q_1, Q_2, \dots, Q_n ). You might want a measure of how much these distributions agree or disagree:
Reasoning:
One approach is to compute pairwise KL divergences ( D_{KL}(Q_i | Q_j) ) to see how different each model’s distribution is. Large pairwise KL might indicate disagreements or that some models are specialized to certain parts of the input space.
Another approach is to compare each model’s distribution to the ensemble-average distribution ( \bar{Q} ), measuring ( D_{KL}(Q_i | \bar{Q}) ).
Pitfalls:
Asymmetry: If you rely on ( D_{KL}(Q_i | Q_j) ), you might interpret large divergences incorrectly if you do not account for direction.
Interpretation: A high KL divergence does not always mean that one model is “wrong,” just that it places mass differently. In classification, for instance, two models might both be correct but highly confident in different classes.
Confidence vs. Calibration: If models are miscalibrated, the KL might reflect large difference in predicted probabilities but not necessarily differences in top-1 predictions.
How does one handle KL Divergence when the parameterization of ( Q ) limits expressiveness, meaning ( Q ) cannot capture important features of ( P )?
This arises frequently in machine learning, especially in approximate inference:
Reasoning:
Suppose ( Q ) is a Gaussian but ( P ) is highly multi-modal. Minimizing ( D_{KL}(P | Q) ) forces the single Gaussian to “cover” the modes, typically leading to a broad distribution that places probability mass over multiple modes. Conversely, if we do ( D_{KL}(Q | P) ), the solution might pick one strong mode (mode-seeking).
Pitfalls:
Underfitting: If the model family for ( Q ) is too restrictive, the best fit might still be a poor representation of ( P ). The KL measure might be misleadingly large simply because ( Q ) cannot represent the shape of ( P ).
Local Minima: Complex distributions can cause the optimization of KL terms to get stuck in local minima if the parameterization isn’t flexible enough or if the optimization method is sensitive to initial conditions.
Remedy: Use richer families of distributions (e.g., normalizing flows, mixture models, or neural parameterizations) that can better approximate the complexity of ( P ). Or consider alternative metrics that might be more stable if the mismatch is primarily about shape, such as Wasserstein distances.
Is KL Divergence suitable for measuring the discrepancy between two distributions when one distribution is an empirical dataset and the other is a generative model that produces samples?
Often, you have a set of samples ( {x_i} ) from the “true” data distribution ( P ), but you can only sample from the generative model ( Q ). Directly computing ( D_{KL}(P | Q) ) or ( D_{KL}(Q | P) ) is not trivial because neither distribution is fully known analytically:
Reasoning:
You could try to approximate ( D_{KL}(P | Q) ) via sample-based methods if you can estimate ( \log Q(x_i) ) for each real data sample ( x_i ). This often happens in maximum likelihood scenarios if ( Q ) is a tractable model (like an autoregressive flow) from which you can compute log probabilities.
If ( Q ) is a black-box generator (like many GANs) and cannot give you explicit likelihoods, you cannot straightforwardly evaluate ( D_{KL}(P | Q) ). You might rely on alternative divergences or approximations (like the adversarial training approach in GANs).
Pitfalls:
No Closed-Form: Some generative models do not provide an explicit density function. Attempting to approximate log-likelihood is challenging or impossible in practice without specialized architecture.
Mode Collapse: If the model is a black-box sampler, a naive approach might not detect that the model fails to generate certain modes of the data distribution (the generator might skip entire regions of data space).
Estimation Error: Attempting to do kernel-based or nearest-neighbor-based density estimation in high-dimensional spaces is error-prone and may not reflect the true divergence well.
In what circumstances does KL Divergence become infinite, and how do we mitigate that in practical implementations?
KL divergence can blow up to ( \infty ) if there exists at least one point ( x ) for which ( P(x) > 0 ) but ( Q(x) = 0 ). In continuous spaces, a similar phenomenon occurs if ( Q ) assigns negligible density to areas where ( P ) has non-negligible density:
Reasoning:
If ( P ) truly has support outside of ( Q )’s support, the term ( P(x) \log \frac{P(x)}{Q(x)} ) becomes unbounded because ( \log \frac{1}{0} \to \infty ).
Pitfalls:
Numerical Instability: In code, you might get NaNs or inf if your predicted probabilities are exactly zero or extremely close to zero for events that actually occur in your data. This can sabotage training or produce meaningless metrics.
Support Mismatch: Even if you think your model can produce all possible outcomes, floating-point issues can cause practical zeros.
Solutions:
Smoothing: Add a small epsilon to ( Q ) so that zero never truly occurs. That is, use something like ( Q(x) + \varepsilon ) as a lower bound in the log denominator.
Regularization: Encourage ( Q ) to be more diffuse so that it doesn’t fully exclude certain events.
Consider Alternative Measures: In some tasks, especially if you expect partial support mismatch, a measure like Jensen–Shannon divergence or the Wasserstein distance might be more robust.
In practical machine learning pipelines, why might one prefer minimizing cross-entropy rather than directly coding up a “KL divergence minimization” objective?
Although cross-entropy and KL divergence are tightly related, direct usage of a “KL divergence term” might involve complexities around computing or estimating ( P \log(P/Q) ). Cross-entropy loss is usually more straightforward to implement:
Reasoning:
For supervised classification, you have discrete labels ( y ). The “true” distribution ( P ) is often a one-hot vector. Minimizing cross-entropy directly is simpler because it is ( -\sum y \log Q ). You skip having to compute ( y \log y ) or a ratio ( \frac{y}{Q} ) that might be undefined if ( Q ) is 0 or if the label distribution is something other than a simple one-hot.
Under the hood, the difference between cross-entropy and KL divergence is just the constant entropy term ( H(P) ), which does not depend on your model.
Pitfalls:
In some custom tasks (e.g., structured prediction, certain generative tasks), you might want to incorporate more sophisticated terms that measure the distribution mismatch in a different manner (like reweighted KL or a partial support domain).
Minimizing cross-entropy is standard for classification, but in certain specialized tasks, direct KL constraints might be more flexible or might operate in latent spaces (like in VAEs).
How can one interpret KL Divergence in the context of policy gradient methods beyond offline RL, such as in trust-region policy optimization (TRPO) or proximal policy optimization (PPO)?
In on-policy RL, methods like TRPO and PPO control how much the new policy deviates from the old policy by bounding or penalizing KL divergence:
Reasoning:
In TRPO, there is a hard constraint ( D_{KL}(\pi_{\theta_{\text{new}}} ,|, \pi_{\theta_{\text{old}}}) \le \delta ). This ensures that each policy update is not “too large,” stabilizing training by preventing catastrophic updates that degrade performance drastically.
In PPO, there is a clipped objective that effectively penalizes big changes in the policy ratio ( \frac{\pi_{\theta_{\text{new}}}(a \mid s)}{\pi_{\theta_{\text{old}}}(a \mid s)} ). This is akin to controlling KL but in a simpler, more practical manner.
Pitfalls:
Balancing Exploration vs. Stability: If the KL constraint (or clipping) is too strict, the policy might learn slowly or converge to a suboptimal local minimum. If it’s too loose, you can get unstable policy updates.
Hyperparameter Tuning: The threshold for KL or the clipping range is typically found via trial and error, and suboptimal settings can hamper performance significantly.
Cost of Computing KL: TRPO’s constraint requires a second-order approximation to KL for large neural networks, which can be computationally expensive.
When dealing with hierarchical models (e.g., mixture models or hierarchical Bayesian models), how is KL Divergence used to compare or constrain distributions at multiple levels?
Hierarchical models often involve latent variables at multiple levels. You might have a prior distribution at one level and a conditional distribution at another:
Reasoning:
One might impose a KL divergence constraint between a conditional posterior and a prior to ensure the learned conditional distribution does not stray too far from some known structural assumption.
In mixture models (like Gaussian mixtures), you might compare each mixture component to a subset of the data distribution or compare the entire mixture to the global data distribution.
Pitfalls:
Nested Divergences: If you have multiple hierarchical layers, the overall divergence-based objective can become quite complex. One might inadvertently push the model too aggressively at the top level while ignoring mismatch at lower layers, or vice versa.
Local Minima: As with many complex models, optimization can get stuck unless carefully initialized or unless specialized inference techniques are applied.
Allocation of Probability Mass: In a mixture model, certain components might get collapsed or overshadowed by others, and the KL measure might not necessarily enforce balanced usage of all components without additional mechanisms.
How can we leverage KL Divergence in data compression scenarios, and what real-world concerns might arise?
KL divergence is connected to the concept of coding length and compression efficiency (via the Shannon coding framework). You might compare the distribution used by a compressor ( Q ) to the true distribution ( P ):
Reasoning:
If ( Q ) is your “code distribution” and ( P ) is the actual distribution of symbols, the average code length is related to ( H(P) + D_{KL}(P | Q) ). Minimizing KL divergence is effectively minimizing the coding redundancy beyond the entropy limit.
Pitfalls:
Mismatch with Real Data: Real data might have correlations or structure not captured by a simplistic ( Q ). The mismatch leads to suboptimal compression rates.
Dynamic or Non-Stationary Data: If ( P ) changes over time (distribution shift), a fixed ( Q ) becomes a poor match, inflating code length. You need to update ( Q ) or adapt it in an online manner, which might be non-trivial if you want to minimize the cumulative KL over time.
Implementation Details: In practical compression systems, we do not usually compute KL directly but rely on learning or explicit coding strategies (like arithmetic coding) that can approximate the distribution with minimal overhead. Numerical issues (like floating-point approximations) can also degrade performance.
How might domain adaptation or transfer learning use KL Divergence to align distributions between source and target domains, and what are tricky aspects?
Domain adaptation tasks often involve a source domain distribution ( P_s ) (where labeled data is abundant) and a target domain distribution ( P_t ) (where data might be unlabeled or scarce). Some methods try to align feature representations by making them similar across domains via a distributional measure such as KL:
Reasoning:
If you embed data from both domains into a latent space, you can try to make the latent representation distributions for source and target close under KL divergence. This might help the classifier or regressor to generalize better from the source domain to the target domain.
Pitfalls:
Label Mismatch: Even if the feature distributions are aligned, the label distributions might differ. Minimizing KL of feature distributions alone might not guarantee good performance if the label marginals shift drastically.
Asymmetry: Choosing which direction of KL might matter if you want to ensure coverage of certain modes in the target domain or ensure you do not ignore sub-populations.
Partial vs. Full Overlap: If the target domain covers only a subset of the source domain’s support or introduces entirely new regions, a naive KL alignment might be misleading.