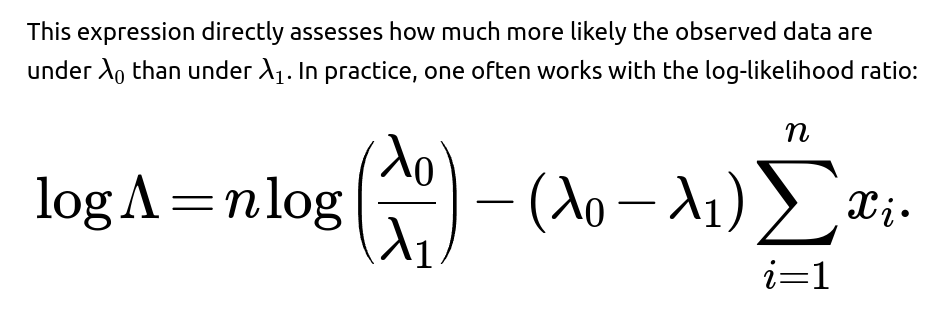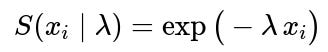ML Interview Q Series: Likelihood Ratio Test for Comparing Exponential Rate Parameters in Lifetime Data

Browse all the Probability Interview Questions here.

20. Say you have a large amount of user data measuring lifetimes, modeled as exponential random variables. What is the likelihood ratio for assessing two potential λ values (null vs alternative)?

Understanding the setup for exponential lifetimes under two different rate parameters

Likelihood ratio for exponential distributions

The likelihood ratio Λ is defined as the ratio of the likelihood under the null hypothesis to the likelihood under the alternative hypothesis. Concretely:

The ratio or its log form can be used in a hypothesis testing framework to decide which of the two rate parameters is better supported by the data.

Deep reasoning on this ratio

The ratio captures two main factors:

• Compute Λ from the data.

• Check if Λ is greater or less than a threshold (often based on a test significance level or an equivalent statistic such as the log-likelihood ratio).

Because exponential distributions are frequently used in survival analysis, engineering reliability, and user-lifetime modeling, this ratio test is a straightforward technique to do quick model comparisons or to test whether usage lifetimes have changed over time.

Code snippet demonstrating how one might compute this ratio in Python

import numpy as np

def likelihood_ratio_exponential(data, lambda0, lambda1):
    """
    Computes the likelihood ratio L(lambda0) / L(lambda1)
    for an exponential model given data and two different rate parameters.
    """
    n = len(data)
    sum_x = np.sum(data)

    # Compute the likelihood ratio
    ratio = (lambda0**n * np.exp(-lambda0 * sum_x)) / (lambda1**n * np.exp(-lambda1 * sum_x))
    return ratio

# Example usage:
data = [2.0, 1.5, 3.1, 0.8, 4.2]
lambda0 = 0.5
lambda1 = 0.6

lr = likelihood_ratio_exponential(data, lambda0, lambda1)
print("Likelihood Ratio:", lr)

Potential real-world pitfalls

When user lifetime data is heavily censored or truncated, the simple product of densities might not fully capture the setting. Censoring adjustments or partial likelihoods might be required. Also, ensure that the exponential assumption is at least approximately valid. In real user-lifetime data, there can be multiple factors such as mixture distributions or non-exponential decay patterns.

Can you talk about how the test statistic is typically used and how to decide on a threshold?

How can we verify the assumptions behind the exponential model before applying the likelihood ratio?

First, checking that the exponential distribution is appropriate is crucial. Common verification techniques include:

• Examining the empirical survival function or the empirical cumulative distribution function and comparing it with the exponential's theoretical curve.

• Checking that the event rate is roughly constant over time. If the rate changes (e.g., if hazard function is not constant), the exponential assumption might fail.

Could there be convergence or numerical stability issues with large datasets?

• Likelihood values might become extremely small, leading to underflow in floating-point arithmetic. Taking the ratio directly might produce 0.0 or NaN if the numbers are too large or too small for machine precision.

• A more stable approach is to use the log-likelihood ratio and then exponentiate only at the final step if needed, or simply keep the comparison in log form without exponentiating.

• In Python, you might prefer computing log⁡Λ and carefully using functions like NumPy’s logaddexp if needed, to maintain numeric stability.

How does censoring affect the likelihood ratio for exponential distributions?

If you have right-censored observations (common in survival analysis), say a user’s lifetime is only known to exceed a certain time but not the exact failure time, the likelihood contribution from that data point becomes

rather than the full PDF. You multiply these survival terms for all censored observations and the PDF for uncensored observations, forming a partial or combined likelihood. The final likelihood ratio test is constructed similarly, except you incorporate the correct form for censored data. This can change the distribution of the test statistic, especially if you do not have a purely complete dataset.

Are there alternative approaches besides a likelihood ratio for comparing exponential rates?

One could consider:

• Bayesian approaches, defining a prior over λ and computing posterior odds.

  

  Non-parametric tests if you do not fully trust the exponential assumption (though with lifetimes, a parametric approach is common if well justified).

Still, the likelihood ratio test remains a straightforward, classical, and powerful approach in many parametric settings.

Below are additional follow-up questions

What if we suspect time-varying rates rather than a constant λ?

In many real-world scenarios, the rate at which users churn (or “lifetime ends”) may not remain constant over time. The exponential model specifically assumes a constant hazard function. If the underlying rate changes, the exponential assumption might not hold. For instance, in user-lifetime data, it is possible that early-stage users might have a higher probability of churn, while more established users become “stickier,” lowering the churn rate over time.

If you still attempt to compare two constant rates, λ₀ vs λ₁, when the true process has time-varying behavior, you risk mis-specification errors. The likelihood ratio derived under the assumption of constant λ may become unreliable. Even if one of the two rates better matches the average churn behavior, neither may fully represent reality. This situation can be exacerbated if the sample is large enough that small deviations from the exponential assumption become statistically significant.

A practical pitfall is ignoring any visible patterns in the data that hint at non-constant hazard. Always inspect whether hazard rates are truly constant. Techniques such as plotting the cumulative hazard over time or applying a parametric survival model that allows for changing rate (like the Weibull or a piecewise exponential) may help confirm or refute the assumption of a single fixed λ. In a more flexible approach, you might compare piecewise-constant or semi-parametric models using a likelihood ratio test that accounts for time-varying pieces.

Could extreme or outlier values in the data drastically affect the likelihood ratio?

An exponential distribution is memoryless but not immune to influence from extreme observations. If you observe unusually large lifetimes, those observations might skew the parameter estimates or make one rate value seem unlikely. For instance, if one or two users remain active for much longer than anyone else, this can push the sum of lifetimes significantly higher, favoring smaller estimates of λ in an MLE setting (if the model is being fit).

When merely comparing fixed rates λ₀ and λ₁, extreme values can swing the likelihood ratio drastically, especially if one λ strongly penalizes very long observations relative to the other. For example, a higher λ expects the data to concentrate on shorter times, so large outliers can yield extremely small likelihood under that hypothesis. Conversely, a smaller λ is more tolerant of large values.

A major pitfall is failing to explore the distribution of the data before applying the test. If your data has a heavy right tail or includes just a few long-lived outliers, the ratio test might be overly sensitive. One solution is to perform sensitivity analyses—remove or downweight outliers to see if the conclusion remains consistent. Another approach is to use robust statistical methods or a heavy-tailed distribution if you truly suspect big outliers are part of the natural data generation process.

How should we handle truncated data, for example if we only record lifetimes above a certain threshold?

Truncation arises if measurements begin only after a certain time has passed, meaning individuals (or users) who “failed” or churned before that time are never observed. If your data is left-truncated, it means you only see those users whose lifetime exceeded some lower bound, say a time point t₀. The correct likelihood for an exponentially distributed random variable X, truncated to be greater than t₀, is

where ( S(t_0 \mid \lambda) = \exp(-\lambda t_0) ) is the survival function at t₀ for the exponential distribution.

When comparing λ₀ vs λ₁, each likelihood must incorporate the adjusted densities for truncated data. If you use the naive density without adjusting for truncation, you risk biasing the test. This might incorrectly favor a model that underestimates the rate because you are not accounting for the fact that you are missing all the users who failed before the truncation point. A subtle real-world example: if you only start tracking user retention after a 7-day free trial, you miss those who left earlier, and your data set is left-truncated. Properly weighting the likelihood ensures you do not distort the parameter comparisons.

Are there any reparameterizations that make interpreting the likelihood ratio easier?

Sometimes it is useful to reparameterize the exponential distribution in terms of its mean μ = 1/λ. This directly relates to average lifetime rather than the rate. Then the density can be written as

In this parameterization, comparing μ₀ vs μ₁ might be more intuitive for domain experts (e.g., telling a product manager “the average user lasts 10 days vs. 12 days”). The likelihood ratio in terms of μ would become

The structure remains similar; you have merely inverted the parameters. The pitfall is ensuring consistency if you switch parameter definitions mid-analysis. You must keep careful track of whether you are using λ or μ throughout the pipeline. Also, many standard reference tables and software packages for LRT-based inference in survival analysis are parameterized in terms of λ, so reparameterizing might require custom code or additional care to avoid confusion.

What if the dataset includes zero or negative values for lifetimes?

In principle, for a lifetime distribution, X ≥ 0 is mandatory. Negative or zero lifetimes typically indicate a data quality problem or a mismatch in the definition of “start time.” If the data inadvertently contains these values—perhaps because the logging system incorrectly recorded churn events or the user joined at one timestamp but was flagged for churn at an earlier timestamp—then the exponential model’s PDF is undefined for negative X and is only borderline meaningful for X = 0 (the PDF can approach λ for X→0).

A pitfall would be to blindly pass such values into your likelihood computation. This can break the math or lead to negative infinite likelihood for that observation, overshadowing the rest of the data. A thorough data-cleaning step is essential. You may need to either remove these cases or correct them if the discrepancy is known to be a logging error. If zero is a genuinely possible outcome (e.g., a user signs up and immediately quits), you might treat it as an extremely small positive number or adopt a mixture model with a point mass at zero plus an exponential tail for nonzero lifetimes.

How does sample size influence the power of the likelihood ratio test?

The asymptotic properties of the likelihood ratio test rely on having sufficiently large samples. When n is large, −2log⁡(Λ) (where Λ is the ratio of likelihoods under H₀ vs H₁) will often follow a well-defined distribution that allows for standard inference. With smaller n, the test may not have enough power to discriminate between two close values of λ, or the distribution of the ratio under H₀ might deviate from the theoretical asymptotic distribution, leading to inaccurate p-values.

In practice, if the sample is very small, you might prefer exact methods or simulation-based approaches (like a parametric bootstrap) to gauge how often one λ outperforms another in repeated samples. If the sample is very large, then even tiny differences in λ₀ vs λ₁ might result in a large difference in log-likelihood, leading to an overly sensitive test that flags small deviations as significant—even if those deviations are practically negligible. A balanced approach is to consider statistical significance alongside effect size, and potentially calibrate the test to domain-meaningful thresholds rather than purely p-value-based thresholds.

What issues might arise if λ₀ and λ₁ are very close together?

If the two rate parameters are nearly identical, the likelihood ratio test might yield a ratio near 1, making it difficult to strongly favor one model over the other. From a practical standpoint, even if your test does produce a statistical difference at a very large sample size, the actual difference in expected lifetimes might be so minimal that it is not actionable.

A subtle pitfall is to fixate on a minuscule p-value without asking whether the difference in lifetimes is meaningful in business or application contexts. For instance, if λ₀ = 0.10 per day and λ₁ = 0.105 per day, the difference in mean lifetimes is 10 vs ~9.52 days, and if you have a massive dataset, you might detect that difference with high significance. But the real-world implication of a half-day shift in average user lifetime may or may not warrant a strategic change. Thus, you should interpret the ratio test in light of domain considerations and effect sizes, not just statistical significance.

When might a parametric bootstrap approach be preferred for significance testing?

In some scenarios, using the theoretical asymptotic distribution for the likelihood ratio might be unreliable—for example, if sample sizes are modest, if there is any boundary condition (like a rate approaching zero), or if the distribution of lifetimes is heavily skewed. A parametric bootstrap approach involves:

• Fitting under one hypothesis (often the null) to obtain a parameter estimate (if the null is composite).

• Simulating many synthetic datasets from that model.

• Computing the likelihood ratio for each synthetic dataset to form an empirical distribution of the test statistic.

• Comparing the observed test statistic to the bootstrap distribution to obtain a p-value or confidence measure.

This approach can capture finite-sample peculiarities and violations of standard assumptions. A potential pitfall is increased computational cost. Generating and evaluating many synthetic datasets can be expensive, especially for large datasets or complicated models. Additionally, you need to ensure you simulate from a model that closely reflects the real data-generating mechanism or at least the null scenario accurately.

How might heterogeneity across user segments complicate comparing two λ values?

A subtle pitfall is misinterpretation: you might reject λ₀ in favor of λ₁ when, in reality, each subpopulation has a distinct rate, and neither λ₀ nor λ₁ matches those varying rates. Another pitfall is that ignoring segmentation can inflate variance or lead to a biased estimate. It is often beneficial to stratify the data or incorporate segment-level random effects (e.g., a hierarchical model) so that the overall test accounts for variation among user subgroups. Otherwise, you may end up with an oversimplified binary comparison that fails to model the underlying complexity.

Could dependencies or correlation within the data invalidate the exponential assumption or the test?

The classical likelihood ratio for exponential distributions assumes independent and identically distributed (i.i.d.) observations. In real-world settings, user churn might be correlated—for example, users might follow each other’s behavior if they are part of a social network, or an external event (e.g., a major competitor’s promotion) could cause a spike in churn across many users simultaneously. This correlation structure means the data is not truly i.i.d.

If there is significant correlation, the standard formula for the likelihood ratio remains a formal ratio, but its statistical properties (like the distribution under H₀) may no longer hold. You could end up with an overly optimistic or pessimistic p-value. As a pitfall, ignoring correlation can cause you to incorrectly reject or fail to reject the null hypothesis.

One approach is to model the correlation explicitly—perhaps using frailty models in survival analysis, where each user might have a random effect capturing unobserved heterogeneity, or using time-varying covariates in a Cox model. If you truly believe the exponential form is appropriate but want to account for correlation, a multi-level or random-effects exponential model can allow partial pooling of parameters across correlated groups of observations. Each approach requires carefully adjusting the form of the likelihood or test statistic to reflect the lack of independence in the data.