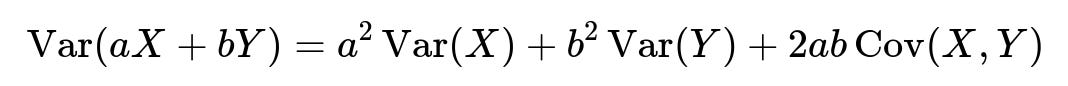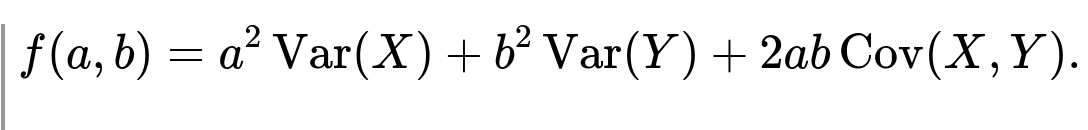ML Interview Q Series: Linear Combinations of Random Variables: Calculating Variance with Covariance
Browse all the Probability Interview Questions here.
Suppose you have two random variables X and Y, both of which have known standard deviations. If you form a new random variable aX + bY, where a and b are constants, what is its variance?
Short Compact solution
One can recall that the variance of a sum of random variables takes into account each variance term as well as their covariance. Also, when scaling a random variable by a constant, the variance scales by the square of that constant. Putting these ideas together:
Hence, the exact value depends on both the individual variances of X and Y and their covariance.
Comprehensive Explanation
Overview of Variance Concepts
Variance measures how spread out a random variable is from its mean. If we have a random variable ( X ), then the variance ( \mathrm{Var}(X) ) is defined as the expected value of the squared deviation from the mean. Formally,
Scaling a Random Variable by a Constant
If we multiply a random variable ( X ) by a constant ( a ), the mean is scaled by ( a ), but the variance is scaled by ( a^2 ). Symbolically:
This arises because when you square the difference ((aX - a\mathbb{E}[X])), the factor (a^2) appears.
Variance of the Sum of Two Random Variables
When adding two random variables ( X ) and ( Y ), one must consider not only the individual variances but also the covariance term:
The covariance term ( \mathrm{Cov}(X,Y) ) quantifies how ( X ) and ( Y ) co-vary. If ( X ) and ( Y ) are positively correlated, this term will be positive; if they are negatively correlated, it will be negative; and if they are independent, the term is zero (assuming independence implies zero covariance).
Combining Both Ideas for ( aX + bY )
Now, if we apply both principles—scaling random variables and adding them—we get:
This is the central formula. It captures how:
(a^2 ,\mathrm{Var}(X)) stems from scaling (X) by (a).
(b^2 ,\mathrm{Var}(Y)) stems from scaling (Y) by (b).
(2ab ,\mathrm{Cov}(X,Y)) accounts for the combined effect of (X) and (Y) on the variance due to their covariance.
Interpretation and Bounds
If (X) and (Y) are independent (so (\mathrm{Cov}(X,Y) = 0)), then the last term vanishes and we get:
If (X) and (Y) are perfectly positively correlated, the covariance term is (+\sqrt{\mathrm{Var}(X)\mathrm{Var}(Y)}), scaled by (ab). This creates the largest possible variance (given a fixed magnitude for (a) and (b)).
If (X) and (Y) are perfectly negatively correlated, the covariance term will be negative, which can reduce the overall variance of the sum.
Practical Example in Python
Although this formula is straightforward, a quick simulation can help confirm it. Here is a Python snippet:
import numpy as np
# Example constants
a = 2.0
b = -1.0
# Generate random samples for X, Y
np.random.seed(42)
X = np.random.normal(loc=0.0, scale=1.0, size=10_000) # mean=0, std=1
Y = np.random.normal(loc=0.0, scale=2.0, size=10_000) # mean=0, std=2
# Sample-based approach
Z = a*X + b*Y
var_estimated = np.var(Z, ddof=1) # ddof=1 for unbiased estimate
# Theoretical approach
var_theoretical = a**2 * np.var(X, ddof=1) + b**2 * np.var(Y, ddof=1) + 2*a*b * np.cov(X, Y, ddof=1)[0,1]
print("Estimated Variance:", var_estimated)
print("Theoretical Variance:", var_theoretical)
In practice, these two values (estimated and theoretical) should be very close, validating our formula.
Potential Follow-Up Questions
How does the correlation coefficient relate to the covariance term in this formula?
The correlation coefficient ( \rho(X, Y) ) is defined as:
In the formula for ( \mathrm{Var}(aX + bY) ), the term involving the covariance can therefore be rewritten as:
This shows that if you only have the correlation coefficient and the individual variances, you can still compute the variance of the sum. It also clarifies how the sign and magnitude of the correlation coefficient directly affect the final variance.
What if X and Y have nonzero means? Does that affect this formula?
The derivation of the variance for a sum of scaled variables does not depend on the means of ( X ) or ( Y ). Variance focuses on the expected value of squared deviations from the mean, and adding or shifting by a constant does not change the variance. So even if (X) and (Y) each have some nonzero mean, the formula
remains valid.
Can we derive confidence intervals around Var(aX + bY) based on sample estimates?
In real situations, ( \mathrm{Var}(X) ), ( \mathrm{Var}(Y) ), and ( \mathrm{Cov}(X,Y) ) might be estimated from finite samples. Each of these estimates has its own uncertainty. Constructing a confidence interval around ( \mathrm{Var}(aX + bY) ) would involve approximating the distribution of these estimates (for example, using the asymptotic normality of sample covariances under certain conditions). Practically, one might use a bootstrap approach:
Bootstrap resampling of the dataset used to estimate ( X, Y ).
For each bootstrap sample, compute (\mathrm{Var}(X)), (\mathrm{Var}(Y)), and (\mathrm{Cov}(X,Y)).
Calculate (\mathrm{Var}(aX + bY)) for each bootstrap replicate.
Use the distribution of these repeated values to form an empirical confidence interval.
What if the distribution of X or Y is not normal?
The formula for the variance of a linear combination of random variables does not require any normality assumptions. It holds for any distribution, as long as variances and covariances exist and are well-defined. Normality often simplifies other analytic tasks, such as forming prediction intervals or analyzing the distribution of the sum. However, the formula for the variance of a sum is always valid if second moments are finite.
Is there a situation where the term 2ab Cov(X,Y) can exceed a² Var(X) + b² Var(Y)?
It is possible for the magnitude of (2ab ,\mathrm{Cov}(X,Y)) to be quite large if (X) and (Y) are strongly correlated. However, it cannot exceed the product of the standard deviations times the factors (a) and (b). More precisely, by the Cauchy–Schwarz inequality and the definition of correlation coefficient:
So the largest possible absolute value of (2ab,\mathrm{Cov}(X,Y)) is:
Whether it numerically surpasses (a^2 \mathrm{Var}(X) + b^2 \mathrm{Var}(Y)) depends on the specific values of (a, b,) and the correlation. In the special case where (\rho(X,Y)=\pm 1), the sum or difference can significantly inflate or deflate the total variance.
How does this knowledge apply in Machine Learning tasks?
In many ML tasks, especially in ensemble methods, you might combine multiple model outputs (which can be seen as random variables) with certain weights, akin to ( aX + bY + \dots ). Understanding how variance adds up when combining predictions can help in analyzing ensemble variance and correlation between models:
Bagging or Bootstrapping: Often assumes independence or near-independence to reduce variance.
Model averaging: If models are positively correlated, the variance reduction from averaging might be smaller.
Diversifying ensembles: Encouraging negative correlation can sometimes reduce overall variance of the ensemble predictions.
All these practical considerations tie back to the same fundamental formula for (\mathrm{Var}(aX + bY)).
Below are additional follow-up questions
What if (a) and (b) are themselves random variables rather than fixed constants?
When (a) and (b) are random, the expression for the variance of (aX + bY) becomes more complicated. Specifically, one must consider:
The variability of (X) and (Y).
The variability of (a) and (b).
Any correlation between (a) and (X), between (b) and (Y), and even between (a) and (b) themselves.
Possible cross-dependencies such as correlation between (a) and (Y) or between (b) and (X).
In particular, if (a) and (b) are independent of (X) and (Y), the variance term would expand to include the expected values of (a^2) and (b^2), as well as the expected value of (ab). One might arrive at an expression like:
Whether it numerically surpasses (a^2 \mathrm{Var}(X) + b^2 \mathrm{Var}(Y)) depends on the specific values of (a, b,) and the correlation. In the special case where (\rho(X,Y)=\pm 1), the sum or difference can significantly inflate or deflate the total variance.
How does this knowledge apply in Machine Learning tasks?
In many ML tasks, especially in ensemble methods, you might combine multiple model outputs (which can be seen as random variables) with certain weights, akin to ( aX + bY + \dots ). Understanding how variance adds up when combining predictions can help in analyzing ensemble variance and correlation between models:
Bagging or Bootstrapping: Often assumes independence or near-independence to reduce variance.
Model averaging: If models are positively correlated, the variance reduction from averaging might be smaller.
Diversifying ensembles: Encouraging negative correlation can sometimes reduce overall variance of the ensemble predictions.
All these practical considerations tie back to the same fundamental formula for (\mathrm{Var}(aX + bY)).
Below are additional follow-up questions
What if (a) and (b) are themselves random variables rather than fixed constants?
When (a) and (b) are random, the expression for the variance of (aX + bY) becomes more complicated. Specifically, one must consider:
The variability of (X) and (Y).
The variability of (a) and (b).
Any correlation between (a) and (X), between (b) and (Y), and even between (a) and (b) themselves.
Possible cross-dependencies such as correlation between (a) and (Y) or between (b) and (X).
In particular, if (a) and (b) are independent of (X) and (Y), the variance term would expand to include the expected values of (a^2) and (b^2), as well as the expected value of (ab). One might arrive at an expression like:
However, additional terms will emerge such as (\mathrm{Var}(a),\mathbb{E}[X^2]) if (a) and (X) are not independent, etc. This is a potentially large expansion, and each cross-term must be handled carefully. Failing to consider the correlation or dependence structures between the coefficients and the random variables can lead to a substantial under- or over-estimate of the true variance.
A frequent pitfall is to ignore the randomness of (a) and (b) altogether and use the simpler constant-coefficients formula. In many practical settings—for example, when (a) and (b) are the outputs of a learned model—they might not truly be constant but random due to the underlying estimation process.
How do we minimize or optimize ( \mathrm{Var}(aX + bY) ) with respect to (a) and (b)?
In certain scenarios, one may want to choose coefficients (a) and (b) to minimize the variance of the combination (aX + bY). The classical approach is to treat ( \mathrm{Var}(aX + bY) ) as a function of (a) and (b). If ( \mathrm{Var}(X) ), ( \mathrm{Var}(Y) ), and ( \mathrm{Cov}(X,Y) ) are known, we can write:
We would then take partial derivatives of (f(a,b)) with respect to (a) and (b), set them to zero, and solve:
Pitfall: One must remember that the solution could be a local minimum or maximum, so we should check the Hessian or reasoning about the shape of the function to confirm it is indeed a minimum.
Edge case: If (\mathrm{Var}(X)) or (\mathrm{Var}(Y)) is zero (for instance, if (X) or (Y) is a constant), the partial derivatives behave differently, and the solution for (a) or (b) might be trivial or unbounded.
In portfolio optimization (a well-known real-world use case), one typically includes constraints like (a + b = 1) (or some other constraints on (a) and (b)) when minimizing variance. Such constraints lead to a constrained optimization, which can be solved with Lagrange multipliers. Not carefully handling constraints can lead to solutions outside a physically or contextually meaningful range.
How does autocorrelation in time series data influence the formula for ( \mathrm{Var}(aX + bY) )?
If (X) and (Y) are time series, the variance at each time point can depend not only on the instantaneous values of (X_t) and (Y_t) but also on past values (autocorrelation). When we write
we typically mean the variance of the distribution at a fixed time point or over the entire stochastic process. In time-series contexts:
(X_t) and (Y_t) could be cross-correlated at various lags. So it’s not only (\mathrm{Cov}(X_t,Y_t)) at time (t) but also (\mathrm{Cov}(X_t,Y_{t-1})) or other lags that might matter when analyzing multi-step predictions.
If one simply takes the formula for two random variables at a single time slice, it remains valid for that particular time slice. However, to generalize to an entire time series, you might need the covariance function or spectral densities across different lags.
Ignoring the autocorrelation structure can be misleading. For instance, if (X) and (Y) exhibit strong seasonality or trends, their covariance might not be consistent across time. One must therefore decide if the formula refers to the unconditional stationary variance or a time-dependent variance.
A significant pitfall is using snapshot-based formulas (like the simple (a^2\mathrm{Var}(X_t) + b^2\mathrm{Var}(Y_t) + 2ab,\mathrm{Cov}(X_t,Y_t))) without acknowledging that over time, correlation patterns may change. In real-world forecasting or time-series modeling, ignoring time dependency can produce an inaccurate picture of how combining forecasts from different models affects overall variance.
Does the formula differ for discrete vs. continuous distributions of (X) and (Y)?
No. The formula for (\mathrm{Var}(aX + bY)) is valid regardless of whether (X) and (Y) are discrete, continuous, or even mixed distributions. The key requirement is that the second moments (i.e., (\mathrm{E}[X^2]), (\mathrm{E}[Y^2])) and the covariance (\mathrm{E}[XY]) exist and are finite. Variance and covariance definitions hold in both discrete and continuous cases:
For discrete distributions, expectations are sums over probabilities: (\sum_x x p_X(x)).
For continuous distributions, expectations are integrals with respect to density functions: (\int x f_X(x) , dx).
A subtle pitfall arises if (X) or (Y) do not have well-defined second moments (for instance, certain heavy-tailed distributions like some Lévy-stable distributions). In such cases, (\mathrm{Var}(X)) or (\mathrm{Var}(Y)) might be infinite, breaking the formula. Similarly, (\mathrm{Cov}(X,Y)) might not exist if the joint distribution is too heavy-tailed.
What happens if either (\mathrm{Var}(X)) or (\mathrm{Var}(Y)) is infinite?
If (\mathrm{Var}(X)) or (\mathrm{Var}(Y)) is infinite (a scenario possible with certain heavy-tailed distributions, such as those with tails heavier than the Pareto threshold for finite variance), the expression (\mathrm{Var}(aX + bY)) is no longer finite. In fact, even if one variable has finite variance, but the other does not, the sum’s variance still remains infinite. Key points:
Infinite variance implies undefined or infinite mean-square: If ( \mathrm{Var}(X) = \infty ), then ( \mathbb{E}[X^2] = \infty ).
Combination with a finite variance variable: If (Y) is well-behaved (finite variance) but (X) has an infinite variance, the sum (aX + bY) also has infinite variance (except in degenerate cases like (a=0)).
Estimation pitfalls: Empirically, if you try to estimate variance from samples of a heavy-tailed distribution, your sample variance might not converge as the sample size grows, leading to potentially large or erratic results.
Real-world examples include financial returns under certain unbounded volatility models or network traffic with extremely large bursts. In these scenarios, standard variance-based risk metrics may be inappropriate, and one might resort to alternative measures like median absolute deviations or distributions that do not assume finite variance.
How do we handle the situation if (\mathrm{Cov}(X,Y)) is undefined or does not exist?
Some distributions or pathological cases can have a finite mean but an undefined covariance. This can happen if the integral defining (\mathrm{E}[XY]) fails to converge. Without (\mathrm{Cov}(X,Y)), the formula:
cannot be applied directly. Potential strategies:
Domain restriction: Sometimes you can consider a truncated version of the random variables or impose conditions on the data to ensure finite second moments.
Alternate metrics: Use robust correlation measures or rank-based correlations (e.g., Spearman’s (\rho) or Kendall’s (\tau)), though these do not directly substitute into the variance formula. They simply provide insight into dependence in cases where classical covariance is not well-defined.
A dangerous pitfall is forcing computations as if covariance did exist, leading to incorrect numerical values or flawed model assumptions.
If we only have partial samples for (X) and (Y) with missing data, how does that complicate estimation of (\mathrm{Var}(aX + bY))?
Missing data can arise when (X) and (Y) are not recorded simultaneously, or some observations of (X) and (Y) are lost. Naively computing sample variances and covariances by ignoring rows with missing data can reduce the effective sample size or introduce bias:
Pairwise deletion: Retaining only data points where both (X) and (Y) are observed might reduce the sample drastically. This is the simplest approach but can lead to less reliable estimates if too many data points are discarded.
Imputation methods: Various methods (mean imputation, regression imputation, multiple imputation) can be used to estimate missing values. However, each method introduces its own assumptions and potential biases.
Maximum likelihood or EM algorithm: In some cases, employing a parametric model and using an expectation-maximization (EM) approach can produce less biased estimates.
A common pitfall is failing to account for the uncertainty introduced by imputing missing values. For example, single-imputation methods might produce point estimates that incorrectly ignore the variability introduced by uncertain data points, thus affecting both (\mathrm{Var}(X)), (\mathrm{Var}(Y)), and (\mathrm{Cov}(X,Y)).
Can the partial derivatives of (\mathrm{Var}(aX + bY)) with respect to (a) and (b) reveal insights beyond just minimization?
Yes. The partial derivatives of ( \mathrm{Var}(aX + bY) ) with respect to (a) and (b) effectively measure how sensitive the total variance is to changes in each coefficient:
Interpretation: If (\frac{\partial}{\partial a}\mathrm{Var}(aX + bY)) is large, it means a small adjustment in (a) can significantly alter the overall variance of the sum.
Local sensitivity: By examining the partial derivatives at the current values of (a) and (b), we see whether a small tweak in either coefficient can reduce or increase risk (if we treat variance as risk).
Symmetry or imbalance: Sometimes, these derivatives show that one variable (say (X)) contributes much more strongly to the variance than the other. That can motivate domain-specific decisions, such as dedicating more resources to stabilizing or smoothing that variable.
A common pitfall is ignoring these local sensitivity measures in practical applications where small changes in model parameters might drastically change the combined variance. This is especially significant in optimization tasks under constraints, like deciding how much capital to allocate between different risk factors in a financial portfolio.
What if we consider (X) and (Y) as high-dimensional vectors and (a) and (b) as scalars?
If (X) and (Y) are vectors (e.g., each is a random vector in (\mathbb{R}^d)), then the variance–covariance concept generalizes to covariance matrices. Specifically:
(\mathrm{Var}(X)) becomes the covariance matrix of (X), denoted (\Sigma_X).
(\mathrm{Var}(Y)) is (\Sigma_Y).
(\mathrm{Cov}(X,Y)) is a cross-covariance matrix (\Sigma_{XY}).
For the linear combination (aX + bY) (where (a) and (b) remain scalars), the new covariance matrix is:
where (\Sigma_{XY} = \Sigma_{YX}^T). Potential challenges:
Dimensionality: As (d) grows, estimating these covariance matrices can be prone to overfitting and require regularization (e.g., shrinkage estimators).
Positive semidefiniteness: We must ensure that the resulting covariance matrix is positive semidefinite. Numerical approximation or sampling noise can lead to indefinite matrices if there is not enough data.
A big pitfall arises when data is high-dimensional but sample size is relatively small, causing covariance estimates to be inaccurate or singular. Practitioners often use techniques like principal component analysis, regularization, or shrinkage to robustly estimate covariance matrices.
How does a small sample size affect the reliability of (\mathrm{Var}(aX + bY)) estimation?
With limited data, the estimates of (\mathrm{Var}(X)), (\mathrm{Var}(Y)), and (\mathrm{Cov}(X,Y)) are prone to higher variance themselves. Consequently, the computed variance of (aX + bY) can be inaccurate in small-sample regimes. In extreme cases, with fewer data points than variables or with strong collinearity, one may see:
Unstable sample covariance estimates: If (X) and (Y) are nearly collinear in a small dataset, the sample covariance might be large in magnitude, possibly skewing any analysis that relies on it.
Overfitting: Especially when the variance is used to make decisions (like in portfolio optimization), small-sample estimates can lead to solutions that look optimal in-sample but perform poorly out-of-sample.
Bias correction: Some formulas use (n-1) in the denominator for variance (the unbiased estimator), but more sophisticated approaches might be needed to reduce bias further when (n) is very small.
It is a common pitfall to trust the naive sample variance and covariance as if they are perfectly accurate with tiny sample sizes. Practical solutions can include acquiring more data, employing Bayesian methods with informative priors, or using shrinkage estimators to impose structure on the covariance estimates.
Under what circumstances does the linearity assumption (aX + bY) break down in real-world settings?
Although the variance formula for a linear combination (aX + bY) is straightforward, real-world processes often involve nonlinear relationships among variables. Examples:
Nonlinear transformations: If you consider something like (\exp(aX + bY)) or polynomials (e.g., (X^2)), the variance formula for a linear combination is no longer directly relevant. You need expansions or advanced methods (e.g., Delta method) to approximate the variance of nonlinear transformations.
Interaction terms: In modeling or regression, you might include an interaction term (c , X \cdot Y). This complicates the variance expression because now your random variable is (aX + bY + cXY), which introduces (\mathrm{Var}(XY)) and additional cross-terms in the covariance structure.
Threshold effects: Some real-world phenomena exhibit threshold or regime-switching behavior, which is not well captured by purely linear assumptions.
A major pitfall is to assume linearity and use the simpler variance formula in contexts where significant nonlinear dependencies or interactions exist. This can lead to underestimating or misunderstanding risk and variability.