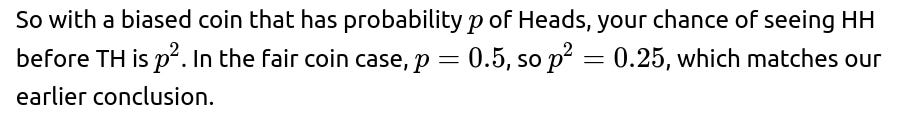ML Interview Q Series: Markov State Analysis for HH vs. TH Coin Toss Sequence Probability
Browse all the Probability Interview Questions here.
16. You and your friend are playing a game. The two of you will continue to toss a coin until the sequence HH or TH shows up. If HH shows up first, you win; if TH shows up first, your friend wins. What is the probability that you win?
One way to analyze this game is by investigating the probabilities of transitioning between states determined by the last coin toss outcome (or no outcome at all if no coin has been tossed yet). The key patterns that end the game are HH (you win) and TH (your friend wins). The goal is to find the probability that HH appears before TH.
It might seem at first glance that each player has an equal chance, or that it might be more complicated to figure out which sequence is more likely to appear first. However, careful analysis or even a direct tree-based enumeration reveals that you have a smaller chance to see HH before TH. The final result is that the probability you win is 1/4.
Below is a detailed reasoning of why that 1/4 value arises, followed by potential subtle points, variations, and possible follow-up interview questions. Every step of logic is shown in detail to illustrate how one can derive the exact probability.
Understanding the Sequences that End the Game
It helps to note that the game stops when either of the following sequences appears in the running list of tosses: HH → You win immediately once two heads appear consecutively. TH → Your friend wins immediately once a tail is followed by a head.
In other words, after every coin toss, you look at the last two outcomes. If they match HH, you win. If they match TH, your friend wins. The question is: which pattern is more likely to occur first?
Approach Using States and Transition Probabilities
A convenient way to dissect this is to define states based on the most recent coin toss (or the initial no-toss state). This approach is reminiscent of a Markov chain, where we track how the process moves from one state to another.
Define three states:
State S: The start state, before any coin is tossed (or equivalently, we can say no partial pattern is formed yet). State H: The last coin toss was Heads (but we have not ended the game yet). State T: The last coin toss was Tails (but we have not ended the game yet).
We do not define separate states for the completed patterns HH or TH because once those appear, the game terminates. They are absorbing outcomes (if HH appears first, you win; if TH appears first, your friend wins).
Let p be the probability of eventually winning starting from S. Let a be the probability of eventually winning if you are currently in state H. Let b be the probability of eventually winning if you are currently in state T.
From state S: If the first toss is Heads (probability 0.5), you move to state H, from which your probability of eventually winning is a. If the first toss is Tails (probability 0.5), you move to state T, from which your probability of eventually winning is b.
Hence, from S we have:
From state H: If the next toss is Heads (probability 0.5), the pattern HH forms immediately, and you win right away. So in that branch, your probability of winning is 1. If the next toss is Tails (probability 0.5), the new last toss is Tails, and we transition to state T, from which the probability of eventually winning is b.
Thus from H:
From state T: If the next toss is Heads (probability 0.5), the pattern TH forms immediately, and your friend wins. That means your probability of eventually winning in that branch is 0. If the next toss is Tails (probability 0.5), you stay in a situation where the last toss is T, so you effectively remain in state T, from which your probability of winning is again b.
So from T:
Solving for b from the last equation:
b = 0.5 * b b - 0.5 * b = 0 0.5 * b = 0 b = 0
This means that once you are in state T, the probability of eventually seeing HH before you see TH is 0. Intuitively, from T, if you ever see a Heads next, your friend immediately wins with TH. If you keep seeing Tails, you stay in T forever, but realistically, the moment you deviate from an endless chain of Tails and see a Head, your friend wins. Therefore, b=0.
Next, solve for a:
a = 0.5 * 1 + 0.5 * 0 a = 0.5
So if you are in state H, your chance of eventually winning is 0.5.
Finally, solve for p:
p = 0.5 * a + 0.5 * b p = 0.5 * 0.5 + 0.5 * 0 p = 0.25
Hence, the probability that HH appears first (i.e., you win) is 1/4. By complement, the probability that TH appears first (i.e., your friend wins) is 3/4.
Another Intuitive Perspective
A direct, intuitive way to see this result is to realize that if the first coin toss is Tails (which happens 50% of the time), you are immediately in state T, and from that point onward, you will lose almost inevitably once an H eventually shows up, because it will form TH. The only way to avoid losing would be to get Tails forever, which has zero probability in an infinite sequence. So effectively, if the first toss is Tails, you lose. The other scenario is that the first toss is Heads (probability 0.5). Then you must get another Head right away (probability 0.5) to lock in HH immediately; if instead the second toss is Tails, you again transition to T, from which you eventually lose with probability 1. That chain of logic also yields a 0.5 * 0.5 = 0.25 chance for you to see HH first.
This 1/4 result can feel surprising, because many might guess that HH and TH could each appear with the same likelihood. But the subtle point is that TH can occur right after a single T, while HH can only occur after an H that is followed by a second H. The presence of T first and then H is often easier to achieve.
Simulation Example in Python
Below is a simple Python simulation that estimates the probability. Running this repeatedly with a large number of trials will generally produce a result around 0.25 for your win probability.
import random
def simulate_one_game():
# States: We only track last toss
last_toss = None
while True:
toss = random.choice(['H', 'T'])
if last_toss is not None:
if last_toss == 'H' and toss == 'H':
# HH appears first => you win
return 1
if last_toss == 'T' and toss == 'H':
# TH appears first => friend wins
return 0
last_toss = toss
def estimate_probability(num_simulations=10_000_000):
wins = 0
for _ in range(num_simulations):
wins += simulate_one_game()
return wins / num_simulations
print(estimate_probability())
If you run this with a sufficiently large number of simulations, you will see the output converge to about 0.25, corroborating the exact theoretical solution.
Edge Considerations
The only potential edge condition that might make someone pause is if you toss Tails forever, in which case the pattern HH never appears and the pattern TH never appears. But that has probability 0 in an infinite sequence of tosses. Therefore, we generally ignore that possibility when computing probabilities. Similarly, from T, you eventually see an H with probability 1 (again ignoring the measure-zero event of infinite tails), so the game will eventually end.
Tricky Points and Why the Probability Is Not 1/2
Many might guess 1/2 for the probability of your winning, reasoning that HH is just as easy to get as TH. But the difference is that HH requires two heads in a row, whereas TH only requires a single tail followed by a head. The “single tail” scenario is easier to initiate than “single head followed by another head,” especially because once a single T is tossed, you become locked in the T state, from which you are destined to lose if an H appears, which is very likely.
Potential Follow-up Questions in an Interview
Below are some questions an interviewer could ask to probe deeper into your understanding of the problem and your familiarity with related techniques.
Follow-up question: Could you solve this by enumerating possible sequences?
You can indeed approach it by listing out the sequences of tosses that might appear and checking in which scenarios you see HH before TH. For instance:
If the first toss is T, eventually you will see TH with probability 1, so that entire branch of sequences leads to your friend winning (except for the zero-probability scenario of infinite Tails).
If the first toss is H, the second toss can be H or T. If it is H, you immediately get HH, and you win. If it is T, you go to T state, eventually leading to TH, so you lose. Hence from the “first toss is H” branch, you only win when the second toss is H.
So enumerating leads to the same 1/4 result. Enumerations typically are easy for short patterns like HH or TH, but if the game had more complicated patterns or partial overlaps, enumerations might become cumbersome, and a state-based approach or Markov chain is usually more scalable.
Follow-up question: Could you modify this problem for different patterns, like HHT vs. THH, and how would the solution generalize?
In general, you would define states that represent partial matches of each pattern. This is a classic technique in analyzing the “First Occurrence of a Pattern” in coin toss sequences. For HHT vs THH, you would have states that denote:
No progress in either pattern yet. A partial match in HHT. A partial match in THH. Possibly more states to represent partially overlapping substrings (such as if you have “HH” and are waiting for T in one pattern, or “TH” and waiting for H in another pattern).
You then define transitions among these states according to the result of the next coin toss. The concept is essentially building a Markov chain or a finite automaton to track partial progress. You solve for the probabilities of hitting one pattern’s absorbing state before the other’s. This is a well-known method in analyzing Penney’s game and various coin-toss pattern competitions.
Follow-up question: Why is the T state so disadvantageous for you in this particular game?
Because from T state, the next coin toss that is a Head (which has probability 0.5 on each toss) creates TH, and that immediately makes your friend win. The only chance to delay losing is to toss T again, but that does not help you progress toward HH. It only keeps you stuck in T. Ultimately, you cannot form HH without first seeing an H, but the moment you see an H from T, that yields TH. Therefore, once the game is in T state, your probability of eventually forming HH first is effectively zero.
Follow-up question: Is there a closed-form approach without states or enumerations?
It is possible to craft an argument based on conditional probabilities, focusing on what happens after the first tosses. The states approach is typically the cleanest to explain. However, one could also reason directly:
If the first toss is T, you will lose (with probability 1 in an infinite sequence). If the first toss is H, then the second toss determines if you immediately get HH (win) or go to T (lose). Hence, probability is 0.5 * (0.5) = 0.25.
Follow-up question: Could you give an example of a real-world pitfall if we tried to rely solely on intuition for patterns like HH vs TH?
One real-world pitfall is to assume that “because both are two-letter patterns and each coin toss is fair, it must be 50–50.” When analyzing repeated random experiments, certain sequences can be more probable to occur first because of how partial overlaps or transitions lock you into a particular losing or winning pattern. In more complex games (like Penney’s game), it can be even more counterintuitive; some seemingly weaker patterns actually have higher probabilities of appearing first. Engineers or data scientists who assume symmetrical probabilities without analyzing partial-overlap transitions might produce faulty results in simulations of repeated random phenomena.
Follow-up question: Could you show code for a more general pattern-matching approach?
Below is a simple Python function that continuously simulates coin tosses and checks for the first appearance of either of two patterns. It can be extended to any pair of patterns. Here, we use it specifically for "HH" vs "TH":
import random
def first_appearance_game(pattern1, pattern2, num_simulations=10_000_00):
# pattern1 is "HH", pattern2 is "TH"
# Returns fraction of times pattern1 appears first
import re
def simulate_once(p1, p2):
tosses = []
while True:
tosses.append(random.choice(['H', 'T']))
current_string = "".join(tosses)
# Check if p1 or p2 appears at the end
# A more efficient approach can track partial matches, but we'll do a direct check for clarity
if current_string.endswith(p1):
return 1
if current_string.endswith(p2):
return 0
wins = 0
for _ in range(num_simulations):
wins += simulate_once(pattern1, pattern2)
return wins / num_simulations
prob_estimate = first_appearance_game("HH", "TH")
print(prob_estimate)
This code does a direct string check. Although less efficient than a Markov chain approach for more complex patterns, it conceptually demonstrates how to test the first appearance of either pattern. When run with a sufficiently large number of simulations, you will again see a result near 0.25 for "HH" vs "TH".
Follow-up question: Would the probability change if the coin were biased?
If the coin is not fair, let the probability of Heads be pp and the probability of Tails be 1−p. Then you would re-construct the same state-based analysis but use pp and (1−p) instead of 0.5 and 0.5. The system of equations becomes:
From state T: Probability of going to TH (friend wins) is pp, so your probability of winning in that transition is 0. Probability of staying in T is (1−p), from which your probability of winning remains b. You get a new equation:
which gives b=0 for any 0 < p < 1 (the only way you wouldn’t lose from T is if p=0, meaning a coin that always lands Tails, but that would never produce HH or TH in normal sense, or is a degenerate scenario). So from T, you are effectively stuck losing if p > 0.
From state H: Probability of going to HH (you win) is p. Probability of going to T is (1−p), from which your probability of winning is b=0. Hence:
From the start state:
Follow-up question: How can this problem be connected to Markov chains or automata for more complex sequence games?
We can generalize by noting that in the pattern “competition” style problem, you typically build a directed graph (or automaton) that tracks how much of each pattern has been seen so far. Each new coin toss transitions you to another state in the automaton. Once you reach the terminal state corresponding to a complete pattern, you know which pattern appeared first. The transition probabilities can be written in a matrix form, turning the system into a Markov chain. Then you can solve a linear system to find the probabilities of reaching each pattern’s absorbing state first. This is exactly the approach used in many pattern-matching probability analyses, such as Penney’s game, coupon collector problems with partial overlaps, etc.
Follow-up question: Could there be any confusion if we had multiple sequences to watch for at once?
Yes, it can become more complicated. Sometimes patterns share partial prefixes or suffixes that can cause unexpected results. For instance, if your pattern is HHH and your friend’s pattern is THH, analyzing which appears first can get tricky because you might see a partial pattern that accidentally also forms part of the other sequence. A thorough technique is always to define states representing exactly how far along each pattern you have progressed. Each coin toss then transitions to the next possible partial match. The mathematics behind it often generalizes from the simpler HH vs TH scenario.
That said, the principle remains the same. You track partial matches, define transition probabilities, and solve. The HH vs TH question is among the simplest forms of such analysis and is a good demonstration of how one might handle more elaborate pattern competition games.
Follow-up question: Are there any subtle real-world scenarios where something like this puzzle might arise?
Any scenario in which we wait for a certain pattern of events to occur in a time series, while a competing event is also possible, parallels the logic of this puzzle. Examples can be found in network error codes (waiting for two consecutive “Success” messages vs. a pattern of “Timeout, then a Recover” message), or in genetic sequences (waiting for a particular motif to appear in the presence of other motifs). In many real-world instances, a naive approach might assume everything is equally likely, but the “first to appear” phenomenon can bias probabilities in unexpected ways—just as we saw with HH vs. TH.
Follow-up question: How does this puzzle exemplify partial overlap considerations, if at all?
In this particular puzzle, there is no direct overlap between HH and TH that we need to consider in the sense of a longer pattern. You cannot “overlap” HH with TH in a single toss the way you might if the patterns were HHH vs. HHT, for example. The entire scenario can be tracked simply by looking at the last toss. However, it does demonstrate that partial knowledge of “the last toss” is crucial for figuring out your next step. In more complex pattern competitions, you often have to track multiple characters of overlap. This puzzle is basically a simpler instance of that broader approach.
Follow-up question: Could you confirm that 1/4 is correct by direct probability arguments without states?
Yes. Another way is:
You only have a chance if you start with H. This occurs with probability 1/2. Then you must immediately get a second H (probability 1/2) to form HH before seeing T. So 1/2 * 1/2 = 1/4. Otherwise, if you toss T at any time once a T has occurred, the next Head will form TH, your friend’s pattern. This direct logic lines up perfectly with the state-based approach and leads to the same answer, 1/4.
Follow-up question: Are there scenarios with no guaranteed ending?
In principle, if the coin were unbiased, it is possible to imagine infinitely many tosses of T (probability zero in the limit) that prevent either pattern from appearing. However, in classical probability, events with probability zero do not affect the final result. So in the real sense, the game terminates with probability 1, making the probability calculations straightforward. If one wanted to be extremely rigorous, you might say that, with probability 1, you will eventually see either HH or TH.
Follow-up question: What is the key lesson for an engineer or data scientist from such a puzzle?
The puzzle highlights that certain outcomes can be deceptively more (or less) likely when we consider who “wins first” rather than raw frequencies of patterns in an entire sequence. It’s a reminder to carefully analyze Markov dependencies and possible states, instead of assuming symmetrical outcomes for patterns of the same length. Real-world processes often have states in which it becomes either very likely or very unlikely for a particular event to happen next, and ignoring that can lead to incorrect conclusions.
Below are additional follow-up questions
What if we only consider the game up to a fixed number of tosses? How does this affect the probability of winning?
If there is a hard cap on the total number of tosses allowed (say we only toss the coin a maximum of N times), then the game may end prematurely before either HH or TH appears. This possibility adds a third outcome: the game may terminate without a winner if neither pattern has shown up within N tosses.
To handle this rigorously, you can track all possible sequences up to length N and see which ones contain HH first, which contain TH first, and which do not contain either pattern by the time you reach N tosses. In a state-based approach, you would add an additional event that the game stops after N tosses regardless of whether a pattern is found. The result is typically that your winning probability is strictly less than 1/4 if N is too small, because you could run out of tosses. For very large N, the probability will approach the full infinite-sequence result of 1/4, since the chance of neither pattern appearing in many tosses becomes very small.
A key pitfall is forgetting to normalize the probabilities among the three outcomes when analyzing a capped game. If you want your final answer to be purely “the probability of winning conditional on the game producing a winner,” you must remove from consideration any sequences that ended without a decisive outcome.
What if the coin toss is replaced by a random draw from a larger categorical distribution, e.g. multiple symbols rather than just H or T?
If you have more than two outcomes per trial (say the “coin” can produce symbols A, B, C, … with different probabilities), then the patterns HH and TH become symbolic strings. For instance, if you only care about seeing the substring “HH” or “TH” among a larger alphabet, you would still define states that represent what you have observed so far and how close you are to each target pattern.
The main conceptual step is that at each draw, you transition to a state based on which symbol was observed. If the symbol is H or T (in the context of your pattern), you move to a more advanced partial match or to a reset. If it is some irrelevant symbol, you might remain in a partial match state or move to a “no progress” state. A potential pitfall is forgetting that certain symbols are “neutral” regarding your target patterns but might break your partial match. The probability calculations follow the same logic as the coin toss problem, just with more possible transitions.
What if the coin can land on its side? Do we incorporate that event into our analysis?
If the coin has a small probability s of landing on its side, then each trial has three outcomes: H with probability p, T with probability q, and Side (S) with probability s, where p + q + s = 1. You need to decide how a side outcome factors into detecting HH or TH. Usually, we might say that the side outcome is simply ignored for the sequence. But ignoring it means you only care about the next H or T that appears, which effectively introduces “skip states.” Alternatively, you might treat S as a literal symbol that interrupts patterns. In that scenario, a partial match might be broken if we get S.
A subtlety is whether the game can remain stuck in side outcomes repeatedly, pushing off the final result. In a large number of tosses, the probability of never seeing H or T might be extremely small if s < 1, but conceptually you still track the effect of these side outcomes. The biggest pitfall is to forget how S might reset partial progress toward HH or TH. If you choose to skip them, you are effectively not using those tosses to progress or break any pattern.
How would knowledge about coin fairness or bias help if players did not know p (the probability of Heads) initially?
In a real-world scenario, if p is unknown, then each player might attempt to estimate it on the fly. With each toss, they update their belief about p. If the coin seems to land Heads frequently, you might favor patterns that start with H. If the coin tends to produce T frequently, that changes your expectation for which pattern is more likely to appear first.
However, in this puzzle, you have no strategic choice over the actual coin toss outcomes, and you cannot alter the sequence. You just observe. The knowledge of p only helps in computing the theoretical probability of seeing HH or TH first. If neither player knew p in advance, they could rely on a Bayesian update for p after each toss, but that doesn’t change the underlying random process. It only changes each player’s predicted probability of winning at each moment in time.
A potential real-world pitfall is if someone incorrectly uses the observed frequencies to re-weight future toss outcomes. If the coin is truly memoryless (even if biased), the probability of H or T remains the same each toss, regardless of past results. But a naive participant might believe in a “hot hand” phenomenon or gambler’s fallacy.
If we expand the game to require three-toss sequences (e.g., HHH vs. THT), how does that generalize?
For patterns of length three, you typically define more states that track partial matches. For instance, if you are looking for HHH or THT, you might have states corresponding to:
No progress: no matching prefix yet. H or T progress: you have matched the first character of a pattern. HH or TH progress: you have matched the first two characters of a pattern. And so on…
Once you reach a complete pattern, the game stops. The probability of HHH appearing first vs THT could be computed by writing down the transitions between partial-match states. Real-world pitfalls arise because some patterns overlap with themselves or each other. For example, the pattern HHH partially overlaps with itself. If you have HH and get another H, that completes HHH, but if you have THT and see another T, you might partially be on track to THT again. The state machine approach is methodical and ensures you do not overlook any subtle overlaps.
What if the sequences we track share partial overlaps, like HHT vs HTH?
Partial overlap can create surprising probability outcomes. For HHT vs. HTH, certain partial progress states can feed into each other in nonintuitive ways. For instance, “HHT” can share a prefix with “HTH” if you look at the latter half of the sequence. In these cases, the best practice is to define states that represent exactly how much of each pattern’s prefix you have matched so far. Then you track transitions carefully, because one or two tosses might shift you from being partially done with one pattern to partially matching another pattern.
The pitfall here is naive enumeration of tosses or naive intuitive reasoning that each pattern is “equally likely.” Overlapping patterns can lead to big asymmetries in which pattern tends to appear first.
Could the game lead to an indefinite loop if we choose certain overlapping patterns?
Even with overlapping patterns, for a fair or biased coin with probabilities strictly between 0 and 1, the probability that you toss infinitely without hitting a terminating pattern is zero in a typical discrete-time Markov chain. Overlaps do not prevent the game from eventually hitting one of the patterns. The only indefinite scenario might be if the coin systematically avoided certain sequences with probability 1, which does not happen for a memoryless coin where p(H) > 0 and p(T) > 0. The subtlety is that a large overlap might cause many repeated near-misses, but eventually one pattern emerges almost surely.
How might we integrate a Markov chain with absorbing states if the game was changed to multiple competing patterns?
For multiple patterns, each pattern can be considered an absorbing state once fully matched. At any state, you keep track of how many characters of each pattern are matched so far. If one pattern becomes fully matched, you transition to the absorbing state for that pattern. You can set up a transition matrix where each row corresponds to a combined “partial match” state, and columns represent the next state after seeing H or T. Once a row corresponds to a complete pattern, that row transitions to an absorbing state. You then solve for the probabilities of being absorbed by each pattern’s absorbing state.
A pitfall is letting the state space blow up if the patterns are large or if you have many patterns in competition. In practice, you build a minimal deterministic finite automaton (DFA) that tracks partial matches efficiently. But the conceptual approach remains the same: it’s a Markov chain with one or more absorbing states, and you find the probability of absorption in each of those states.
Could you analyze the expected time to absorption and does that help conclude which pattern is more likely to appear first?
Yes, you could compute the expected number of tosses before one of the patterns shows up by summing the expected times to absorption from each state. However, the expected time alone does not directly tell you which pattern is more likely to appear first. You might find, for example, that one pattern appears first more frequently, but the other pattern typically takes fewer expected tosses when it does happen. So while analyzing expected time is a valuable exercise, it is the probability of hitting each absorbing state that directly answers “which pattern is more likely first.” One pitfall is to conflate “shorter average waiting time” with “higher probability” of being the winner, which can be very misleading in some pattern competition problems.
What if side bets or partial rewards are introduced before the game ends?
Suppose you define a rule: if we ever see HT (not leading to the final TH, but just a partial snippet), a small side payout is triggered, or similarly if we see a single H after the start, a side payout triggers. The analysis becomes more complicated because you track not only which pattern ultimately wins but also which partial patterns have occurred so far for side payouts.
In principle, you still use a Markov chain approach, but with additional states or additional tracking of whether certain side conditions happened. You can accumulate an expected reward for each possible path. The main pitfall is ignoring the fact that partial patterns can occur multiple times in different contexts, so you need to be careful not to double-count or miscount how side bets accumulate. Keeping precise track of partial match states remains the best approach to avoid confusion.
Could you discuss how to quickly run a real-time simulation to see who is leading at each toss, and what pitfalls arise?
A real-time simulation could keep a rolling window of the last one or two tosses (for the HH vs. TH game) and check if a winning pattern has just occurred. To see who might be “leading,” you might track how close each pattern is to appearing. In practice, for HH vs. TH, “leading” is somewhat trivial because if the current state is T, your friend is effectively on the verge of winning if the next toss is H. If the current state is H, you are halfway to HH, so a next-toss H would let you win.
A pitfall of real-time checking is forgetting that the next toss might abruptly shift the advantage. Another pitfall is stopping the simulation too early and trying to extrapolate. Because the game ends the moment one pattern appears, partial progress can be overturned in a single toss.
If we repeated the game many times, could the fraction of times you win deviate significantly from 1/4 in finite samples?
Yes, in a finite number of games, sampling variance can cause deviations from the true probability. With repeated trials, the fraction of your wins converges to 1/4 as the number of trials goes to infinity (by the law of large numbers). In practical finite runs, you might see something like 0.23 or 0.27, especially if the total number of games is modest.
A pitfall is drawing a strong conclusion from a small sample, e.g., if you get lucky and see HH first in the first few trials, you might believe the theoretical probability is higher than 1/4. Another pitfall is ignoring potential biases in the random number generator if you simulate on a computer.
What if each coin toss was subject to measurement error or sensor noise?
In physical scenarios (like a coin toss read by a noisy sensor), you might not always accurately record H or T. If the sensor incorrectly classifies T as H with some small probability ε, then your observed sequence might differ from the real coin outcomes. If you define “HH” or “TH” based on the recorded data, you have effectively introduced a non-Markov process from the viewpoint of the observer. You might need to incorporate hidden states: the true coin toss is a Markov chain, and the measured outcome is a noisy observation. The game ends when you observe HH or TH, which may not reflect the true coin toss pattern.
A subtle pitfall is that the observer might see HH even if the real sequence was TH due to sensor error. This can mislead the final outcome. The analysis becomes more complex, involving hidden Markov models if you want the probability distribution of actual events.
How does the gambler’s fallacy or gambler’s ruin concept show up in this scenario?
A gambler’s fallacy might appear if a participant believes that after a T toss, the chance of H next is higher or lower than 0.5 (for a fair coin). This is an erroneous assumption because each toss is independent. It could lead someone to misjudge the likelihood of “switching” from T to H, which is exactly how TH arises. Gambler’s ruin ideas revolve around states of “fortune,” but here your “fortune” is not typically tracked as a numeric total. However, you could interpret the state S/H/T as analogous to the gambler’s partial progress. There is no conventional gambler’s ruin boundary here, but the core pitfall is letting the gambler’s fallacy warp your sense of the unconditional independence of tosses.
Could we represent the states as a 2x2 matrix for transitions, ignoring the absorbing states?
You can build a small transition matrix for (S, H, T). However, once HH or TH appears, you leave the chain, so those are absorbing states not included in the 2x2 submatrix. Typically, you create a 3x3 or 4x4 matrix that includes your absorbing states. For example, define states S, H, T, W (win), L (lose), where W and L are absorbing. The transitions from S, H, T to either themselves or the absorbing states can be laid out. Then you can solve for the fundamental matrix in Markov chain absorption analysis. A subtle pitfall is forgetting to include the absorbing states or incorrectly normalizing transitions if you skip them.
How does correlation between consecutive tosses affect the logic?
If tosses are not independent—say you have a Markov chain for coin outcomes (Heads, Tails) with some correlation—then the probability of a Head following a Head might be different from the unconditional probability of a Head. You would define a higher-level chain that tracks (Last toss was H) or (Last toss was T), but with different transition probabilities for H → H, H → T, T → H, and T → T. You still want to see which pattern HH or TH arises first, but you must incorporate these new probabilities into your transitions.
One subtlety is that from T, the next toss being H might be more or less likely than 0.5 depending on correlation. Another subtlety is that the stationary distribution might not be 50-50 for H vs. T. The final probability of seeing HH first vs. TH first could shift significantly. A real-world pitfall is applying the memoryless formula for a process that actually has correlation, leading to incorrect results.
If multiple players each wait for a different pattern, how do we handle who wins first?
You can track the progress of each pattern simultaneously in a combined state machine. The first pattern that hits completion wins. If you have three or more patterns, you need to track partial progress for all of them. This can get large quickly but follows the same logic: define a combined state that encapsulates how many characters of pattern1, pattern2, pattern3, etc. are currently matched. At every new symbol (coin toss), you update the partial matches. If one pattern completes, that player wins.
A pitfall is letting the state space blow up combinatorially if patterns share partial overlaps. Another pitfall is ignoring that it’s possible for more than one pattern to complete on the same toss if they share the final symbol. Usually, if that happens, you might define tie-breaking rules or say that the pattern with highest priority wins. Handling that scenario carefully is essential.
Could large deviation theory or Chernoff bounds help in analyzing times for these patterns?
Chernoff bounds and large deviation theory are typically used to bound the probability that certain random events deviate from their expected frequencies over many trials. They do not directly tell you which pattern appears first in a short sequence. However, they might help estimate how long it takes until the probability that the pattern has not appeared is extremely small. For instance, you could argue that the probability of not seeing HH or TH by n tosses shrinks exponentially in n. But that does not specifically address the ratio of probabilities of HH vs. TH.
A subtle pitfall is trying to use large deviation bounds to claim something about “which pattern occurs first” in short sequences. Those bounds typically become meaningful for large n, and often these patterns occur quickly in practice.
What if the players can pay or choose to skip certain tosses?
If you allow a player to “skip” a toss, effectively you are removing that toss from the sequence. This would be akin to controlling the process so that you do not see certain outcomes. The problem transforms significantly, because it introduces strategy. For instance, if you are close to losing (e.g., the last toss was T in the HH vs. TH game), you might want to skip the next toss to avoid the risk of getting an H that leads to TH. But if you skip forever, you never progress. You would have to define a cost function for skipping or a rule limiting the number of skips. Then you can model it as a stochastic control problem, analyzing expected payoff.
A pitfall is ignoring that skipping might just delay the inevitable. Another pitfall is forgetting to define whether the friend can skip as well or if only one player has that power.
Are there real-world applications that hinge on partial signals, akin to HH vs. TH, that could affect sequential detection?
Yes. In sequential detection or sequential hypothesis testing, you often watch a stream of sensor data for a certain “signature.” If your competitor is looking for a different signature, the first to confirm their signature might trigger an alarm, a system shutdown, or some action. Each signature can be considered a pattern. The HH vs. TH puzzle is a simplification of real detection problems where partial data might strongly hint that you’re close to one signature, but a single contradictory measurement might pivot you closer to a competing signature.
A subtlety is that real data might not be purely binary or memoryless. There might be noise, correlation, or hidden states. The fundamental concept of “first to appear” remains, but you add layers of complexity. A pitfall is building a purely theoretical Markov chain ignoring real noise distributions.
Could we apply Bayes’ Theorem in a more advanced way here?
In principle, you can phrase the event “HH appears first” in terms of a Bayesian perspective: “Given the infinite sequence of coin tosses, what is the posterior probability that the first occurrence of either pattern is HH?” But that typically reduces back to the direct Markov chain or enumeration argument. Bayes’ Theorem is more relevant if you have priors on the coin’s bias or uncertain knowledge of the process. For example, if you do not know p, you could place a prior on p and then compute the posterior probability that HH appears first after each toss. But once you fix p, the Markov chain approach is simpler. A pitfall is conflating Bayesian inference about p with the frequentist question of the actual probability of HH vs. TH in the real coin process.
If the sequences were continuous signals, does “first occurrence” logic still apply?
If you have a continuous-time signal with states, you can still define a stopping time when your pattern is first observed. Then you can set up a state-based or differential equation approach for transitions in continuous time (a continuous-time Markov chain or semi-Markov process). The fundamental concept of “which pattern do we detect first?” remains. The difference is that you’d use transition rates instead of transition probabilities per discrete toss. A pitfall is failing to adapt the mathematics of discrete transitions to continuous rates, possibly leading to an incorrect or incomplete model.
What if you can pay a penalty to terminate the game early? How does that tie into optimal stopping?
An optimal stopping version would say: “At any point, you can end the game and take a certain payoff.” For instance, if the last toss is H and you think the next toss might be H (giving you a 50% chance to win immediately), you might weigh that expected value against the penalty of continuing. This transforms the problem into a sequential decision under uncertainty, reminiscent of the standard gambler’s ruin or the secretary problem, except the payoff depends on which pattern might appear first.
A pitfall is ignoring that once you stop, you might forfeit the possibility of a big payoff if HH eventually occurs. The analysis would revolve around dynamic programming, computing the expected payoff for continuing vs. stopping.
In repeated gameplay, does the fraction of times you win converge to 1/4, or are there hidden edge effects?
Over many independent repetitions of the game, the fraction of times you get HH first converges to 1/4 by the law of large numbers (assuming a fair coin). “Hidden edge effects” typically do not persist across fully independent games. However, if the coin’s fairness changes from one round to another, or if knowledge gleaned from previous games influences something about future tosses, you might not see the exact 1/4 in practice. Another edge condition is if the coin gets physically damaged or players suspect cheating, changing the distribution of outcomes. But in a theoretically controlled environment with a consistent fair coin, yes, the fraction will converge to 1/4 as the number of repeated games grows.
How do we test the random number generator’s fairness in a large-scale simulation?
One approach is to apply standard randomness tests (like DIEHARD or TestU01) or simpler tests like a chi-square test on the frequency of Heads vs. Tails. You can also look for patterns in the output, autocorrelations, or runs tests. For the HH vs. TH puzzle, if the generator is biased or correlated, your empirical fraction might deviate from 1/4. A pitfall is running only a small number of games, seeing 1/4 exactly, and concluding the generator is perfect. In practice, you need robust statistical analysis to be sure there are no hidden correlations or irregularities that might skew results over time.
If each coin toss result could be ambiguous, leading you to guess H or T, how would you incorporate that?
If you have an ambiguous toss result, you might guess whether it was H or T. This guess might be correct or incorrect with some probability. This is akin to sensor noise or partial observability. You end up with a hidden Markov model in which the unobserved “true toss” is either H or T, and your observed toss is H, T, or “ambiguous.” You can define observation probabilities. The probability of eventually seeing “HH” or “TH” from the observer’s perspective is no longer a straightforward Markov chain on the actual tosses. One pitfall is to treat ambiguous results as “skip.” Another is to treat them incorrectly as either H or T deterministically, which can systematically bias your detection of patterns.
Could the logic of HH vs. TH break down if the coin is physically manipulated (e.g., flipping method influences outcomes)?
Yes, real coins can be manipulated to produce Heads or Tails with higher probability if the flipping technique is not random. The puzzle’s analysis assumes an idealized random process with no knowledge or influence from the players. If a player can manipulate or guess the next outcome, the entire probability distribution changes. A pitfall is ignoring that some players might develop a skillful toss that lands heads more often, thus increasing the likelihood of H sequences. This is an extreme scenario but relevant in actual coin-flipping contexts.
Could we approach the problem with expected values of a payoff function that depends on which pattern appears first?
Yes. If the payoff to you is 1 if HH appears first and 0 if not, your expected payoff is the probability that HH appears first, which is 1/4. Your friend’s expected payoff is 3/4. If there were more elaborate payoffs—like you gain X if HH appears first, the friend gains Y if TH appears first, or partial payoffs for partial patterns—then you sum across the respective probabilities. The pitfall is that you might try to do a naive ratio of partial pattern frequencies, which does not necessarily match the chance of first occurrence. Only the probability of first occurrence yields the correct expected payoff.
If the coin tosses form a hidden process with Markov switching states, how does that complicate “first pattern to appear”?
In a Markov switching model, the coin might be fair most of the time, but it occasionally switches to a “biased mode” where Heads is more likely, then back again. The mode changes according to some Markov chain. From the outside, you still observe a sequence of H or T, but the probability distribution changes over time. To track HH or TH, you might need to define states for (current mode, partial match progress), resulting in a two-level Markov chain. The pitfall is ignoring the possibility that if you are in a heavily biased-for-Heads mode, HH might appear very quickly, or if you are in a T-preferred mode, TH might become more likely. The analysis can become much more intricate, but the principle of “define states carefully and track transitions” remains.
Could the puzzle mislead a human into thinking the sequences are equally likely?
Yes. A common pitfall is to see that both target patterns have length two and conclude they each have a 50% chance of occurring first. This confusion arises because if you look at all possible two-toss sequences in isolation, HH and TH are just two among four equally likely outcomes (HH, HT, TH, TT). But that misses the dynamic aspect: you keep tossing until the pattern emerges. The presence of T pushes you into a losing state (from your perspective) more quickly, because as soon as the next toss is H, your friend wins with TH. The big lesson is that “which pattern appears first” is not the same as “which pattern is likely among short toss sequences in isolation.”