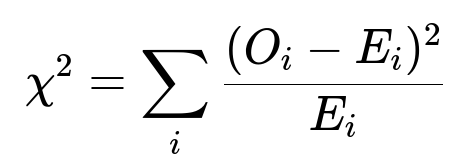ML Interview Q Series: Modeling Supreme Court Vacancies Using the Poisson Distribution and Chi-Square Test.
Browse all the Probability Interview Questions here.
Vacancies in the U.S. Supreme Court over the 78-year period 1933–2010 have the following history:
48 years with 0 vacancies
23 years with 1 vacancy
7 years with 2 vacancies
0 years with ≥ 3 vacancies
Test the hypothesis that the number of vacancies per year follows a Poisson distribution with some parameter λ.
Short Compact solution
The parameter of the hypothesized Poisson distribution is estimated as λ = 37/78 vacancies per year. The data are grouped into three categories: 0 vacancies, 1 vacancy, and ≥ 2 vacancies. Using the Poisson pmf, the expected numbers of years in these groups turn out to be approximately 48.5381, 23.0245, and 6.4374, respectively. A chi-square statistic with 1 degree of freedom is computed as 0.055, which corresponds to a high p-value of about 0.8145. Therefore, the Poisson model with λ = 37/78 fits the observed data very well, and we fail to reject the hypothesis that the yearly number of Supreme Court vacancies follows a Poisson distribution.
Comprehensive Explanation
Overview of the Poisson Distribution
The Poisson distribution is often used to model the probability of a number of events occurring within a given time interval when these events occur independently and with a constant average rate. The probability of observing k events given parameter λ (the average rate) is:
Here:
λ is the average (expected) number of events per unit time (in this case, vacancies per year).
k is the observed count of events (vacancies) in a given year.
e is the base of the natural logarithm.
k! is the factorial of k.
Estimating λ
From the data, there are a total of 78 years and a total of 37 vacancies over that entire period. A natural estimator for λ is simply the average number of vacancies per year:
λ = (total number of vacancies) / (total number of years) = 37/78
Grouping the Data
We observe:
48 years with 0 vacancies
23 years with 1 vacancy
7 years with 2 vacancies
0 years with 3 or more vacancies
To perform a chi-square goodness-of-fit test, we typically combine categories if the expected counts in any category are too small. Here, 0 and 1 vacancies have sufficient counts, but 2 or more vacancies are grouped as one category (≥ 2 vacancies), because only 7 years have 2 vacancies and none has ≥ 3. This grouping ensures we have more robust expected counts in each category.
Computing Expected Counts
If X follows a Poisson(λ = 37/78), then:
p0 = P(X = 0) = (λ^0 e^(-λ)) / 0! = e^(-λ)
p1 = P(X = 1) = (λ^1 e^(-λ)) / 1!
p2plus = 1 - p0 - p1 (covers X ≥ 2)
Multiplying these probabilities by the total number of years (78) gives the expected frequencies in each category:
Expected 0-vacancies years = 78 * p0
Expected 1-vacancy years = 78 * p1
Expected ≥ 2-vacancies years = 78 * p2plus
Plugging λ = 37/78 into these expressions yields approximately:
0 vacancies: 48.5381
1 vacancy: 23.0245
≥ 2 vacancies: 6.4374
The Chi-square Statistic
To test goodness of fit, we use the chi-square statistic:
where:
O_i is the observed count in category i.
E_i is the expected count in category i.
Since we have 3 categories but estimated 1 parameter (λ) from the data, the degrees of freedom are: (3 categories) − (1 estimated parameter) − 1 = 1
The observed vs. expected counts are:
0 vacancies: O=48, E≈48.5381
1 vacancy: O=23, E≈23.0245
≥ 2 vacancies: O=7, E≈6.4374
Hence the chi-square statistic is: (48 − 48.5381)² / 48.5381 + (23 − 23.0245)² / 23.0245 + (7 − 6.4374)² / 6.4374 ≈ 0.055
Determining the p-value
A chi-square value of 0.055 with 1 degree of freedom corresponds to a large p-value (roughly 0.8145). A high p-value indicates that the observed data deviate very little from what is expected under the Poisson model with λ = 37/78. Thus, there is no statistical evidence to reject the hypothesis that the number of vacancies per year follows a Poisson distribution.
Practical Computation in Python (Illustration)
import math
import scipy.stats as stats
obs_counts = [48, 23, 7] # Observed (grouped)
lam = 37/78 # MLE for λ
p0 = math.exp(-lam)
p1 = lam * math.exp(-lam)
p2plus = 1 - (p0 + p1)
exp_counts = [78 * p0, 78 * p1, 78 * p2plus]
chi2_stat = sum((o - e)**2 / e for o, e in zip(obs_counts, exp_counts))
p_value = 1 - stats.chi2.cdf(chi2_stat, df=1)
chi2_stat, p_value
Follow-up question 1: Why are categories sometimes combined in a chi-square test?
When dealing with a chi-square goodness-of-fit test, each expected count E_i must typically be large enough (a common rule of thumb is at least 5) so that the chi-square approximation is valid. If some categories have very small expected counts, we combine them with adjacent categories to ensure that each category has a sufficiently high expected count. In this problem, we combine years with 2 or more vacancies into one category because the frequency of ≥ 3 vacancies is zero, and counting a separate category for 2 vs. 3 or more would produce very small expected counts.
Follow-up question 2: What would happen if the p-value had been very small?
A small p-value (for example, < 0.05) would indicate that the observed frequencies deviate significantly from the expected Poisson frequencies given the estimated λ. In that scenario, we would reject the hypothesis that vacancies follow a Poisson distribution. We would then consider alternative distributions or investigate additional factors that might affect the likelihood of a Supreme Court vacancy in a given year (such as justices’ ages, health, or external historical events).
Follow-up question 3: How does estimating λ from the data affect the degrees of freedom?
Whenever we estimate parameters from the data before performing a chi-square goodness-of-fit test, we lose degrees of freedom. The general rule is to subtract 1 for each parameter estimated. Here, because we estimated λ directly from the total number of observed vacancies, that lowers our degrees of freedom from (number of categories − 1) to (number of categories − 1 − number of estimated parameters). That is why the degrees of freedom here is 1 instead of 2.
Follow-up question 4: Could a different grouping strategy affect the test outcome?
Yes. In practice, the way you group the counts can influence the calculated chi-square statistic. If categories are grouped differently—especially around the tail events where expected counts can be small—there might be small differences in the p-value. However, typically the grouping is done in a way to respect distribution structure (like combining rare events) and to avoid overly small expected counts. The fundamental conclusion usually remains similar if the distribution truly fits well.
Follow-up question 5: What if expected counts in a category are extremely low?
If an expected count is extremely low, the chi-square approximation might become inaccurate. In such cases, either:
Categories should be combined until each expected count is sufficiently large.
An alternative exact test or simulation-based method can be applied.
In this Supreme Court vacancy example, combining the category “≥ 2 vacancies” keeps the expected count well above 5, so the usual chi-square approach remains appropriate.
Below are additional follow-up questions
Follow-up question 1: How would we address a scenario where the data might be over-dispersed or under-dispersed relative to the Poisson assumption?
When a dataset shows over-dispersion, it means the sample variance of the counts is larger than the sample mean, which is a violation of the Poisson assumption (Poisson requires the mean and variance to be equal). Under-dispersion is the opposite problem (variance is smaller than the mean). A classical remedy is to consider alternative models such as:
The Negative Binomial distribution (over-dispersed case).
Quasi-Poisson approaches in a regression context.
Zero-inflated Poisson or other mixture models if there are more zero-count observations than expected.
Each approach attempts to account for the extra or reduced variation. For instance, in a Negative Binomial model, an additional parameter controls the dispersion. In zero-inflated models, some observations may come from a “structural zero” process, so the usual Poisson does not adequately capture the high frequency of zero counts. Practitioners detect these issues by comparing the sample mean and variance or by fitting a Poisson model and investigating the residual pattern. If significant deviations from Poisson are found, they look at more flexible models.
A potential pitfall occurs when ignoring over-dispersion. The model might appear to fit well in the central categories but fails in the tails, leading to an incorrect conclusion about the underlying data-generating mechanism. Conversely, with under-dispersion, the model might systematically overestimate tail probabilities. Hence, it is crucial to verify the equality of mean and variance in the observed data, or at least do a more thorough residual check, before concluding that a Poisson distribution is appropriate.
Follow-up question 2: What if the probability of a vacancy is not constant over time (e.g., due to changing court sizes or retirement patterns)?
In many real-world settings, the rate λ may not be stable across the entire observation window. For instance, changes in court size, average tenure lengths, or historical events (resignations, expansions, etc.) could alter the expected number of vacancies per year. A simple Poisson assumption with a single fixed rate may fail to capture a trend or piecewise changes in λ.
One approach is to use a time-varying Poisson model (or Poisson regression), where λ depends on covariates or on the year. For example, if we suspect that after a certain decade there were more retirements, we might segment the data into different periods and estimate a separate λ for each segment. Another solution is to include relevant covariates (such as the average age of the justices) in a regression-based Poisson framework.
A key pitfall: ignoring time dependence and treating the entire 78-year period as homogeneous can mask patterns. You might incorrectly conclude a good fit because overall summary statistics line up, but in reality, there might be short intervals with significantly different vacancy rates. Examining the data over smaller time segments or using a formal model selection procedure can help detect such time dependence.
Follow-up question 3: How would you handle zero-inflation when certain years are structurally guaranteed to have no vacancies?
Sometimes, external constraints can force certain years to have zero vacancies (e.g., laws, official policies preventing new appointments under some circumstances, or extremely rigid appointment structures). This creates a situation where there are “too many” zeros compared to a standard Poisson process. A zero-inflated Poisson (ZIP) model is a common approach. The ZIP model effectively assumes two processes:
With probability p, a year belongs to the “structural zero” state (no vacancies occur).
With probability (1 − p), a standard Poisson(λ) process determines whether or not a vacancy occurs.
To fit this model, maximum likelihood methods or Bayesian techniques can estimate both p (the probability of a forced zero) and λ (the average rate of vacancies in the “non-structural-zero” years). If the data exhibit a cluster of zero counts in certain years, simply applying a standard Poisson analysis might incorrectly yield a poor fit or might artificially deflate λ.
A subtle pitfall arises if there is confusion between “truly zero for structural reasons” versus “zero simply because the random process did not produce a vacancy.” Failing to distinguish these can mislead the analysis or cause misestimation of λ.
Follow-up question 4: How would dependencies between successive years affect the test?
Poisson processes typically assume independent increments. In other words, the number of vacancies in one year should not affect the number of vacancies in another. However, in real-world Supreme Court data, there may be correlation across years. For instance, if a justice retires in one year, the probability of another justice retiring the following year might change (they may decide to wait or coordinate retirements).
When the data points (yearly vacancy counts) are not independent, the chi-square test for the Poisson model might be invalid because the test assumes independence. In such cases, a Markov-dependent model or a Poisson autoregressive model might be more appropriate. For instance, you could explore models where λ in year t depends on the number of vacancies in year t−1.
A key pitfall is to apply the standard chi-square test ignoring correlation, leading to biased p-values. Typically, correlation inflates or deflates the variance in the data, causing the test to be miscalibrated. Thus, if correlation is suspected, you would employ more advanced time-series or random-effects models that specifically handle dependent count data.
Follow-up question 5: What if certain extreme outliers or single-year anomalies exist?
Even though the maximum observed vacancy count is 2 in the given dataset, one might wonder about outliers in other contexts (e.g., a scenario with 4 or 5 vacancies in a single year that drastically shifts the average). Rare outliers can heavily influence the Poisson parameter estimate if the dataset is small.
If an extreme observation occurs (like a sudden high count in one year due to extraordinary circumstances), the Poisson model might overestimate λ when fit across the entire period, potentially inflating expected counts in other years. In practice, investigators might:
Perform a sensitivity analysis by excluding the outlier year to see whether the conclusion changes.
Consider a robust method or a mixture model that accounts for unusual spikes.
A big pitfall is to blindly accept the single high-count event as typical and shift the entire distribution, thereby underestimating the probability of zero or one vacancy. The opposite can happen if an outlier is artificially suppressed when it is actually valid—leading to underestimating the true variability in the data.
Follow-up question 6: Could lack of power be a concern with relatively few observations in some categories?
Even though we have 78 total years, certain categories (like 2 or more vacancies) might have very few events. This can create a “lack of power” problem: if the test has few data points in that tail, it might not detect moderate but real deviations from the Poisson assumption.
A low-power test can fail to reject the null hypothesis even when the data are genuinely non-Poisson. To address this, you might consider:
Combining multiple smaller categories (as we did for ≥ 2) to ensure each category has enough observations for reliable testing.
Using a simulation-based approach to assess how frequently the test might fail to detect differences of a given magnitude.
Collecting data over a longer period or combining data with other relevant sources if appropriate.
A subtlety is that a non-significant result does not always mean “the model is correct.” It can also mean “we do not have enough evidence to say otherwise.” Practitioners should interpret a high p-value with caution and also look at effect sizes, confidence intervals for λ, and residual diagnostics.
Follow-up question 7: Is there a scenario where an exact Poisson test would be preferable to a chi-square approximation?
A chi-square test is already an approximation that can break down if expected counts in categories are small. In cases where the sample size is modest or many categories have low expected counts, an exact goodness-of-fit test (based on enumerating all possible outcomes or using Monte Carlo methods) may be more accurate. Such exact tests do not rely on the asymptotic distribution of the test statistic and can be especially relevant for small or sparse datasets.
The pitfall is that exact tests may be computationally expensive if the data are large or if the state space of possible outcomes is huge. However, if the dataset is small or if you can combine categories effectively, an exact method can yield more reliable inferences. Another possibility is to use a parametric bootstrap, repeatedly simulating from the fitted model and computing how often the observed statistic or something more extreme is found, thereby getting a more robust estimate of the p-value.
Follow-up question 8: Why might we also consider a likelihood ratio test to compare models?
While the chi-square test is a standard approach, a likelihood ratio test (LRT) provides another formal mechanism for comparing nested models. For example, you might compare:
A simple Poisson model with parameter λ.
A more complex model, say a two-parameter Poisson regression with a time-varying effect.
The LRT involves computing the difference in log-likelihoods of the two models (one nested within the other), and comparing that difference to a chi-square distribution with degrees of freedom equal to the difference in the number of free parameters. This approach can be more flexible if your interest is in comparing multiple models rather than simply assessing fit against a single hypothesized distribution.
Potential pitfalls arise if the nested models do not meet the regularity conditions for the LRT or if the data are too sparse for reliable parameter estimation in the more complex model. Additionally, when models include boundary parameters (for instance, mixing proportions that can be zero), the usual chi-square reference distribution may not be accurate, so careful checks or simulation-based methods may be needed.
Follow-up question 9: How do we interpret the result if the estimated λ is close to zero?
If the observed average number of events (vacancies) is extremely low and thus λ is near zero, most of the probability mass in the Poisson distribution will be concentrated at zero vacancies. It is then crucial to see if the (few) non-zero observations align with the tail probabilities of the Poisson. If there is a mismatch, it might indicate a data generation mechanism not well captured by a single Poisson parameter.
One major pitfall is that when λ is very small, even a single outlier (like 2 or 3 events in a short time span) might drastically shift how we perceive the distribution. Low λ also amplifies the possibility of zero inflation or structural zeros. In such scenarios, you should examine the distribution of the non-zero data carefully to see if they align with a Poisson(λ) or if a different approach is required.
Follow-up question 10: How might the test conclusions change if we used a Bayesian approach to estimate λ?
A Bayesian approach places a prior on λ (e.g., a conjugate Gamma prior), then updates this prior with observed data to get a posterior distribution for λ. We could then use posterior predictive checks to assess how likely the observed vacancy data are under the posterior predictive distribution. This method can be more flexible when data are sparse: the prior can shrink unrealistic estimates or incorporate external knowledge (e.g., historical patterns or expert judgment about typical vacancy rates).
The pitfall is that the conclusion can be sensitive to the choice of the prior. A poorly chosen or uninformative prior might lead to posterior estimates similar to the frequentist approach, but a very strong prior might overshadow the data. Analysts need to conduct sensitivity checks by varying the prior assumptions to confirm the robustness of any conclusion about Poisson fit.