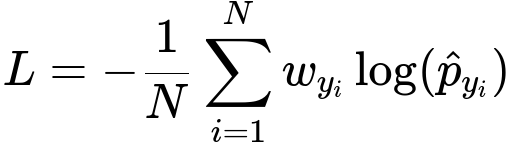ML Interview Q Series: Name some methods you know for Rebalancing a dataset using Rebalancing Design Pattern

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Rebalancing a dataset is crucial when dealing with class imbalance in supervised learning. Class imbalance can cause many algorithms to perform poorly because most standard loss functions and evaluation metrics assume each class has equal importance or frequency. Rebalancing strategies help address this by adjusting how samples from each class are used during model training. Below are several common rebalancing techniques and their underlying logic.

Oversampling the Minority Class

When the dataset has one or more classes that are underrepresented, one straightforward way to fix this imbalance is to replicate (or resample) the instances of those minority classes. Tools like RandomOverSampler in Python's imbalanced-learn library can duplicate minority samples or use more sophisticated approaches to create synthetic examples. A potential issue is that exact duplication of minority samples may lead to overfitting, although it ensures the model sees enough instances of the minority class.

Undersampling the Majority Class

Instead of oversampling the minority classes, one can reduce the size of the majority class. This ensures each class is represented at roughly the same level. However, it can lead to information loss since many majority-class samples are discarded. This method is simple and can be suitable when abundant data is available in the majority class, and computational constraints or memory limitations demand a reduced dataset size.

Synthetic Data Generation (SMOTE and Variants)

SMOTE (Synthetic Minority Oversampling TEchnique) creates new, synthetic data points for underrepresented classes by interpolating between existing minority-class samples. SMOTE looks for near neighbors within the feature space of the minority class and forms synthetic points to improve class representation. Variants, like SMOTE-NC (for nominal and continuous attributes) or Borderline-SMOTE, refine how the synthetic samples are generated, focusing on more informative regions. These techniques can reduce the overfitting risk associated with naive oversampling.

Data Augmentation

For domains such as computer vision or natural language processing, data augmentation is an alternative approach. It involves domain-specific transformations (e.g., rotation, flipping, cropping for images; synonym replacement for text) to increase the effective size of the minority class. This preserves the essential label while diversifying the input, mitigating overfitting and rebalancing the dataset without discarding valuable majority-class data.

Class Weighting in the Loss Function

Adjusting the loss function to assign a larger penalty to misclassifying minority classes is another way to handle imbalance. When a data instance from a minority class is misclassified, the model is penalized more severely, forcing the model to pay extra attention to underrepresented classes. In many libraries (such as scikit-learn or TensorFlow), setting class weights in the training function is relatively straightforward.

Below is the generic weighted cross-entropy formula used in classification. This formula is central when implementing cost-sensitive learning:

In this equation:

• N is the total number of training samples.

• y_i is the actual label of the i-th sample, and hat{p}_{y_i} is the predicted probability for the correct class y_i in plain text.

• w_{y_i} is the weighting factor assigned to class y_i in plain text. A higher weight is typically assigned to underrepresented classes.

• The logarithm log(...) is taken of the predicted probability of the correct class to calculate the loss.

When the model observes a minority-class example, w_{y_i} is larger, so any misclassification error contributes more to the overall loss. This drives the model to learn decision boundaries that better account for minority classes.

Focal Loss

Another variant is Focal Loss, which extends the idea of weighting to focus more on “hard” misclassified examples. Focal Loss was originally introduced to tackle severe class imbalance in object detection tasks. It modifies cross-entropy by adding a modulating factor that lessens the penalty for well-classified examples, focusing training on the minority samples that are most difficult to classify.

Hybrid Methods

In real-world practice, combining multiple techniques can sometimes yield the best results. For instance, one might use SMOTE followed by a slight undersampling of the majority class and also employ a cost-sensitive learning objective. It is always crucial to monitor the validation performance through metrics such as F1-score, AUC-ROC, or precision-recall curves to confirm that rebalancing strategies have genuinely improved the classifier’s performance.

Practical Implementation Example

Below is a simplified Python illustration demonstrating how to use oversampling or undersampling with the imbalanced-learn library, combined with scikit-learn for modeling:

from imblearn.over_sampling import RandomOverSampler
from imblearn.under_sampling import RandomUnderSampler
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from collections import Counter
import numpy as np

# Suppose X, y are your features and labels
X = np.random.rand(1000, 10)
y = np.array([0]*900 + [1]*100)  # Imbalanced dataset

X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.2)

print("Original training label distribution:", Counter(y_train))

# Oversampling example
oversampler = RandomOverSampler(random_state=42)
X_train_over, y_train_over = oversampler.fit_resample(X_train, y_train)
print("Oversampled training label distribution:", Counter(y_train_over))

# Train a random forest on oversampled data
clf_over = RandomForestClassifier()
clf_over.fit(X_train_over, y_train_over)
y_pred_over = clf_over.predict(X_test)
print("Classification Report (Oversampling):")
print(classification_report(y_test, y_pred_over))

# Undersampling example
undersampler = RandomUnderSampler(random_state=42)
X_train_under, y_train_under = undersampler.fit_resample(X_train, y_train)
print("Undersampled training label distribution:", Counter(y_train_under))

clf_under = RandomForestClassifier()
clf_under.fit(X_train_under, y_train_under)
y_pred_under = clf_under.predict(X_test)
print("Classification Report (Undersampling):")
print(classification_report(y_test, y_pred_under))

In this example, we apply either RandomOverSampler or RandomUnderSampler to adjust class distributions before training. Both strategies aim to handle class imbalance but do so differently, hence it is essential to compare various rebalancing approaches.

How to Decide Which Technique to Use

The choice among oversampling, undersampling, SMOTE, weighted loss, or a combination depends on:

• Available data quantity and its diversity.

• The importance of minority-class recall versus overall accuracy.

• The risk of overfitting or information loss.

• The computational cost of training.

Real-world usage often involves a combination of these methods, guided by validation metrics and domain-specific constraints.

Follow-up Question: How does one handle data leakage issues when rebalancing?

Data leakage can occur if the rebalancing process is performed before splitting into training and testing (or cross-validation) sets. To avoid contaminating the validation or test data:

• Always split the dataset into train and test (or cross-validation folds) first.

• Apply the rebalancing technique only to the training set.

• Keep the validation/test set distribution untouched to reflect real-world performance.

Follow-up Question: When might you prefer cost-sensitive learning over explicit resampling?

Cost-sensitive learning modifies the loss function to place a higher penalty on errors for underrepresented classes. This approach avoids duplicating or discarding samples but requires the loss function and optimizer to handle class weights. It is often preferred if:

• You have sufficient data and do not wish to artificially replicate or drop samples.

• You aim to preserve the distribution of majority classes while still emphasizing minority classes.

• Your training framework easily supports custom class weights or advanced loss functions like Focal Loss.

On the other hand, if you have a small dataset or face memory constraints, oversampling or undersampling might be simpler. Combining both cost-sensitive learning and resampling is also a viable strategy, especially for severely skewed data.

Follow-up Question: How do you assess the impact of rebalancing in a model pipeline?

Use specialized evaluation metrics that better capture performance under imbalance:

• F1-score: Harmonic mean of precision and recall, highlighting performance on minority classes.

• Precision-Recall AUC: Often more informative when there is a large class imbalance, focusing on minority classes’ precision and recall.

• ROC AUC: Provides a broader view of classifier performance across different thresholds.

• Confusion matrix analysis: By comparing misclassified minority samples versus majority samples, you can identify if rebalancing improved minority-class predictions without severely hurting overall accuracy.

Validation metrics should be compared across various rebalancing strategies. If the model’s performance on the minority class improves without excessively degrading results on the majority class, you have a net gain.

Follow-up Question: Is it possible to use advanced synthetic oversampling in deep learning tasks (like in PyTorch or TensorFlow)?

Yes, data augmentation and synthetic oversampling can be used with deep learning frameworks. For images, standard augmentation transforms (random cropping, flipping, color jittering) can be composed in torchvision.transforms in PyTorch or tf.image in TensorFlow. For NLP tasks, strategies like back-translation or synonym replacements can generate new text samples. SMOTE can also be integrated as a preprocessing step, especially for tabular data. The key is to ensure no data leakage and to experiment with different oversampling or augmentation parameters.

Below are additional follow-up questions

How can class imbalance be handled in a multi-class setting where more than one class is underrepresented?

In a multi-class scenario, imbalance manifests not just between a single minority class and a majority class, but potentially among several classes with varying degrees of representation. A major pitfall is trying a one-size-fits-all approach. For example, if you apply a simple random oversampling technique to all minority classes equally, you might overshoot and artificially inflate some classes too much. Instead, the following points need careful consideration:

One approach is to treat each underrepresented class separately. You could, for instance, define separate sampling ratios or class weights. Class weighting can be extended by assigning different weights to each class, often proportional to 1 / (class frequency). This ensures that rarer classes receive higher emphasis during training but does not necessarily cause extreme overfitting if tuned properly.

A subtlety is that different classes might exhibit unique data distributions and complexities. For instance, a rare but highly variable class might benefit more from synthetic oversampling (like SMOTE) than simple random replication. Conversely, a class that is only slightly less frequent might be adequately rebalanced with a smaller weighting factor instead of an extensive synthetic oversampling.

Another pitfall is that, in high-dimensional settings, it can be challenging for techniques like SMOTE to generate truly informative samples. You might unintentionally create outliers if the classes are not well-clustered in feature space. Therefore, always validate each rebalancing step through metrics like macro-average F1-score or macro-average recall. These metrics treat each class equally, allowing you to see if certain rebalancing techniques overly favor some classes while harming others.

When does rebalancing risk hurting overall model performance?

Rebalancing can hurt overall model performance when it either introduces noise or removes too much useful data. Oversampling the minority class by exact duplication can lead to overfitting, especially if the minority class has very limited examples. The model may memorize those oversampled examples rather than learn generalizable patterns.

Similarly, undersampling the majority class can weaken the model’s decision boundary by discarding valuable information. If the majority class is diverse, removing many samples may cause the model to miss critical sub-clusters or nuances, reducing overall accuracy for that class. The net effect is often a decrease in performance on the majority class that must be carefully weighed against gains in minority-class performance.

A subtle but important edge case arises when you rebalance a dataset that is not truly representative of real-world conditions. For example, if your original production data reflect a genuine frequency of classes, rebalancing might create a mismatch between training and inference-time distributions, causing the model to misjudge real-world data. Monitoring the model in production with real data distribution is essential to detect such discrepancies.

Is rebalancing always the best strategy in scenarios with extremely rare classes?

When a minority class is extremely rare—say, less than 1% of the data—oversampling might not alone solve the problem. In some domains (e.g., fraud detection, anomaly detection), the nature of the rare class is fundamentally different from regular instances. Traditional oversampling methods may produce synthetic samples that don’t capture the intricate “abnormal” patterns accurately.

A potential approach is to use anomaly detection techniques, where the model learns what “normal” data look like and flags anomalies. If you decide to use rebalancing, you must ensure you are not creating unrealistic synthetic anomalies. One pitfall is that your synthetic oversampling method might inadvertently create data points that look too similar to normal instances, effectively confusing the model.

Cost-sensitive learning can help in extreme cases by focusing on punishing errors for the rare class more heavily. This can be combined with specialized metrics—like the confusion matrix’s false negatives and false positives specifically for the rare class—to gauge how well the model captures those outliers. Additionally, domain knowledge is crucial. If you can isolate rules or known patterns about the rare class, you might incorporate them as constraints or features rather than purely rebalancing data.

How do you handle rebalancing in time-series data or sequential data?

In time-series or sequential tasks (e.g., predicting anomalies in sensor readings over time), rebalancing must preserve temporal ordering. A key pitfall is randomly oversampling minority events, which might break natural chronological relationships. If you replicate a rare sequence segment and insert it in random places within a training set, you risk distorting the time dependencies the model needs to learn.

A more nuanced approach is to perform any oversampling or undersampling in a way that retains local temporal structure. For instance, you can replicate entire temporal windows containing rare events instead of single time points. However, you should do this carefully to avoid introducing duplicated patterns that don’t align with the real temporal flow.

Another subtlety is ensuring you split data by time before rebalancing. If you sample from future data and leak it into earlier training data, you compromise the chronological integrity. This can lead to an overly optimistic estimate of model performance. Validation should be done with a proper time-series split, keeping the rebalanced training data strictly separated in time from the validation and test sets.

What if the imbalance shifts over time in live or streaming data scenarios?

In streaming data or live systems, class distributions may change (also known as concept drift). A model trained on a rebalanced snapshot of historical data could become outdated as soon as the real-world distribution shifts. For example, a fraud detection system might see new fraud techniques that alter the minority-class patterns.

One approach is to adopt online learning or incremental training methods that continuously update the model and rebalancing strategy. For instance, you might apply a sliding window over recent data to dynamically perform oversampling or cost-sensitive adjustments based on the latest distribution. A pitfall is rebalancing too aggressively on short windows, leading to drastic fluctuations in the model. Another risk is ignoring the fact that an increasing frequency of the once-rare class means your original rebalancing method might no longer be relevant.

Monitoring performance metrics in real-time is crucial. If you observe consistent drops in recall for the minority class, it might indicate that class distribution or characteristics have changed. At that point, reevaluating your rebalancing pipeline—potentially even re-designing it—is essential to ensure the model remains robust.

Can rebalancing negatively affect interpretability or feature importance?

Rebalancing might make certain model interpretability methods less straightforward. For example, consider a decision tree or random forest model that bases feature importance on frequency-based metrics (like Gini impurity). If you drastically oversample the minority class, some features may appear artificially more or less important.

A hidden pitfall is that feature importance can shift if minority samples are repeated. The algorithm sees these oversampled rows more often, possibly biasing splits. The same is true of model-agnostic interpretability methods, such as SHAP values, since the distribution of training examples has been altered from the real-world environment. Domain experts, therefore, need to interpret feature importances or local explanations with caution, recognizing that the training data are not in their original distribution.

A potential approach is to examine feature importance both before and after rebalancing. If the insights drastically change, investigate whether the new perspective reveals genuine underappreciated patterns or is simply an artifact of rebalancing. Also, employing methods like cost-sensitive learning does not alter the dataset distribution itself and thus can preserve interpretability aspects related to sampling—though the model’s decision criteria still shift due to weighting the classes differently.

What if the data exhibits multiple types of imbalance within multiple labels or tasks (like multi-label classification)?

In multi-label settings, each instance can simultaneously belong to several classes, and imbalance patterns could vary across labels. It’s possible that certain label combinations are rare or that a label is rarely present but highly correlated with another label. A naive strategy of rebalancing each label in isolation might break these correlations or create unrealistic label co-occurrences.

A recommended strategy is to carefully examine the label co-occurrence matrix. You might discover that some label pairs are extremely rare, while others are common. Techniques akin to SMOTE can be adapted to multi-label data by generating new samples that maintain label dependencies. However, those methods can be tricky to tune, and it’s easy to end up producing synthetic samples that do not reflect plausible label combinations.

A subtlety arises when we try to do partial rebalancing: maybe certain underrepresented label combinations are critical for the task, while others are not. In that scenario, you might selectively oversample only those minority label combinations deemed most relevant. Evaluating success must then go beyond single-label precision and recall metrics, looking at multi-label metrics such as the subset accuracy or macro-averaged F1 across all labels. This ensures that the rebalancing strategy has improved performance where needed without drastically harming more frequent label combinations.

What are the primary considerations when applying rebalancing to highly dimensional data, such as large-scale text or image embeddings?

When data are very high-dimensional—like deep neural network embeddings of images or large text documents—many rebalancing strategies can create misleading samples or cause the “curse of dimensionality.” SMOTE and other interpolation-based methods might form synthetic samples that don’t lie in a meaningful manifold region if points are too sparsely distributed.

In these cases, domain-specific data augmentation is usually more effective. For example, in computer vision, transformations like rotations, flips, color shifts, or adding noise can generate new, valid images for the minority class. In NLP, back-translation or synonym-based augmentation can produce variations of text in a relatively realistic way. A key pitfall is that domain-specific transformations must preserve the label: augmentations that alter the fundamental content or meaning of the sample can lead to noisy labels and degrade performance.

In extremely high-dimensional problems, it’s also advisable to evaluate if dimensionality reduction or specialized embedding methods could help. If you reduce the data to a more compact latent space (for instance, using autoencoders), you might then apply rebalancing in this lower-dimensional space to create synthetic samples that more realistically capture the minority class distribution. However, caution is warranted if the latent space itself is poorly learned or merges distinct sub-clusters.

How can you systematically test different rebalancing strategies and select the best one?

A robust approach is to create a pipeline that includes:

1. Splitting data correctly into train, validation, and test sets.

2. Applying a variety of rebalancing methods (e.g., oversampling, undersampling, SMOTE variants, cost-sensitive learning) to the training data.

3. Training identical model architectures on each rebalanced variant.

4. Evaluating on the same validation set using multiple metrics, including F1-score, precision-recall AUC, and confusion matrix analysis.

5. Checking for overfitting by comparing performance between training and validation sets.

A common pitfall is to fixate on a single metric—like accuracy—which can be misleading under class imbalance. Instead, you want to ensure the chosen metric truly reflects performance trade-offs, such as false negatives versus false positives for the minority class. If multiple rebalancing strategies appear to work similarly on validation data, testing with a final holdout set or even running a small pilot in production can highlight differences that weren’t apparent during offline experiments.

Another subtlety is hyperparameter tuning. Techniques like SMOTE have parameters for the number of nearest neighbors, and cost-sensitive frameworks have class-weight hyperparameters. You can tune these parameters using cross-validation. Overlooking this tuning step might lead to suboptimal or excessive rebalancing. Once you finalize your selection, careful documentation of each step ensures reproducibility and provides transparency to stakeholders about why a particular rebalancing approach was chosen.