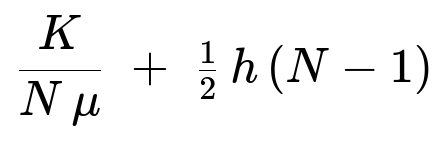ML Interview Q Series: Optimal Batch Sizing for Stochastic Production Systems Using Regenerative Process Analysis.
Browse all the Probability Interview Questions here.
At a production facility orders arrive one at a time, where the interarrival times of the orders are independent random variables each having the same distribution with expected value μ. A production is started only when N orders have accumulated. The production time is negligible. A fixed cost of K>0 is incurred for each production setup and holding costs are incurred at the rate of h·j when j orders are waiting to be processed. Identify a regenerative stochastic process and find the long-run average cost per unit time as a function of N. What value of N minimizes the long-run average cost per unit time?
Short Compact solution
Consider the time between two successive production runs as one regenerative cycle. Because we wait for N orders to accumulate, the expected length of each cycle is N μ. During each cycle, a fixed setup cost K is incurred, plus holding costs. The expected holding cost results from each of the N arrivals waiting an average of (N – i) μ for i in 1..N, leading to a total expected cost in one cycle of
K + (1/2) h N (N – 1) μ.
Dividing by the expected cycle length N μ gives the long-run average cost per unit time:
Minimizing this over real N>0 shows that the optimal solution occurs near
and so the best integer choice of N is whichever integer is closest to that value.
Comprehensive Explanation
Regenerative Process Identification
A regenerative process is a stochastic process that restarts itself in a probabilistically identical way at certain random time points. In this problem:
Each production run acts as a regeneration point.
Right after a batch of N orders is processed (production time is assumed negligible), the system “resets” to zero pending orders and must accumulate another N orders before running production again.
Thus, we model each cycle from just after one production run to just after the next. These cycles are i.i.d. because the interarrival times of orders are independent and identically distributed.
Length of One Cycle
Since orders arrive one by one, each cycle must collect exactly N orders. Let μ be the expected interarrival time of a single order. Because the interarrival times are i.i.d. with mean μ, the expected time to accumulate N orders is N μ.
Hence, the expected length of one cycle is simply N μ.
Costs Incurred During One Cycle
There are two main cost components within each cycle:
Setup (production) cost Every time we initiate production, we pay a fixed setup cost K.
Holding (waiting) cost If j orders are waiting, the cost rate is h j per unit time. Over the entire waiting period for all N orders, we sum up the holding costs for each order i, where i runs from 1 to N.
The i-th arriving order waits until the remaining N − i orders arrive.
On average, waiting time for the i-th order is (N – i) μ.
Hence, the holding cost for the i-th order is h (N – i) μ.
Summing over i from 1 to N:
Sum of holding cost in one cycle = h μ [ (N – 1) + (N – 2) + … + 1 + 0 ]. The sum of these integers 1 + 2 + … + (N – 1) is (N – 1) N / 2. Thus,
Expected holding cost in one cycle = h μ ( (N – 1)N / 2 ) = (1/2) h N (N – 1) μ.
Including the fixed setup cost K, the total expected cost in one cycle is:
K + (1/2) h N (N – 1) μ.
Long-Run Average Cost per Unit Time
By the renewal-reward theorem, the long-run average cost per unit time is the total expected cost per cycle divided by the expected length of the cycle. Since the cycle length is N μ, we have:
Hence, the long-run average cost per unit time is
Finding the Optimal N
To find an optimal N>0 that minimizes the average cost, one approach is to treat N as continuous (call it x) and then later select the nearest integer. Define the function
g(x) = K / (x μ) + (1/2) h x for x>0.
We differentiate g(x) with respect to x, set that to zero, and solve for x:
Derivative: d/dx [ K / (x μ) + (1/2) h x ] = –K / (x² μ) + (1/2) h.
Set it equal to zero: –K / (x² μ) + (1/2) h = 0 => (1/2) h = K / (x² μ) => x² = (2 K)/(h μ) => x = sqrt(2 K/(h μ)).
Since N must be an integer in practice, we usually take N to be the integer closest to sqrt(2 K/(h μ)).
Follow-up Questions
How does this relate to common inventory models?
The formula for N* = sqrt(2K/(h μ)) is analogous to the Economic Order Quantity (EOQ) formula in inventory theory, often written as sqrt(2DK/H) under different notations. Here:
K is analogous to the “setup” or “ordering” cost.
h is analogous to the “holding” cost per unit per time.
μ is the demand rate’s reciprocal (interarrival time).
The result that the optimal batch size is proportional to sqrt(K/h) is quite standard in production and inventory management.
What if the interarrival times are not identically distributed or have a different known distribution?
The renewal-reward framework primarily requires that each cycle is identically distributed and independent of the others (renewal property). As long as the mean time to get N orders is N × E[T] for some T (the single interarrival time random variable), the same approach holds. The key point is that the expected cycle time is the sum of N i.i.d. interarrival times. If those i.i.d. times remain the same distribution (possibly not exponential, but still with a finite mean), the mathematics for the expected cycle length remains valid. If they are no longer i.i.d., or if their distribution changes over time, we lose that simple renewal property, making the analysis more complicated.
What if the production (setup) time is not negligible?
If each production run itself takes a random time with some expectation p, then this p must be added to the cycle length. In that scenario, the expected cycle length becomes N μ + p. Likewise, if there is any waiting or holding cost incurred during production, that should be included in the total expected cost in one cycle. The renewal-reward theorem would still apply, but the formula for costs per cycle and cycle length would differ slightly, changing the final expression for the average cost and thus the optimal N.
Could we have a backlog if the holding space is finite?
In real-world scenarios with limited waiting space or partial backlogs, the problem might change from one purely about “waiting cost” to one that may also involve lost sales or penalty costs. The formula for the total cost in each cycle would then need to incorporate costs associated with lost orders or backlogged orders. However, as long as each cycle resets at production time, a similar regenerative structure can be preserved, and you could adapt the same renewal-reward logic. But the explicit expression for cost per cycle would become more complex.
How robust is the solution if K or h changes over time?
The solution depends directly on K (setup cost), h (holding cost rate), and μ (the mean interarrival time). If any of these drift or vary with time, the process may no longer remain stationary, and the straightforward renewal-reward approach might not reflect the real average cost. In practice, one might re-estimate these parameters periodically and recalculate a new optimal N as they change.
By understanding these nuances and carefully applying the renewal-reward theorem, we can confidently find the optimal batch size N that minimizes the long-run average cost, and adapt the model to accommodate variations in arrival distribution, production time, and cost structures.
Below are additional follow-up questions
How would the analysis change if there is a maximum allowable waiting time for any order?
If there is a strict policy that no single order can wait longer than a certain threshold (call this W), then whenever we hit that waiting-time limit (even if fewer than N orders have arrived), we must start production. This policy enforces a time-based trigger in addition to the quantity-based trigger. As a result:
We lose the simple “wait for exactly N orders” cycle structure if the maximum waiting time is exceeded before collecting N orders.
Each cycle potentially ends either when N orders arrive or when the first order is about to exceed the waiting limit W, whichever occurs first.
The expected cycle length and expected total cost per cycle become more complicated because production can be triggered by either condition.
A renewal-reward framework can still be used if we define regeneration points at production start times, but the distribution of the cycle length is a mixture of two scenarios (time-based vs. quantity-based).
To find an optimal policy balancing the risk of excessive wait times and the cost advantages of larger batch sizes, one typically solves an optimization problem that involves both the batch-size decision and the time-limit policy. In many real systems, a combined approach is used (e.g., “start production when we have N orders, or when the oldest order is X hours old, whichever happens first”).
Key pitfall: If W is too small, you lose the economies of scale from batching. If W is too large, you might incur huge holding costs for those early arrivals. Practical systems often have to fine-tune this balance.
What if the holding cost rate h itself is a function of time or the number of orders in the queue?
In the original model, the holding cost rate was assumed constant h per order per unit time. If, however, h changes dynamically—say, h is higher at times of peak congestion or if there are quantity-dependent storage costs—then:
For j orders in queue, the cost rate might be f(j) instead of j h, where f(j) could be non-linear. For instance, storage cost might escalate once capacity thresholds are exceeded.
We can still compute the expected total holding cost by summing the area under the queue-length curve multiplied by the per-unit cost function. However, the algebra often becomes more involved if f(j) is non-linear.
If f(j) is known and consistent across cycles, the system can still be treated as regenerative at production completion. But deriving a closed-form solution for the optimal N might be more difficult.
One may need to rely on approximate methods (e.g., numerical optimization or simulation) to find the batch size N that minimizes the long-run cost.
Pitfall: Assuming a constant h when in reality it is a step function or a continuous increasing function can lead to suboptimal decisions in practical settings.
Could there be a random setup cost K in each cycle, and how would that affect the solution?
If K is not fixed but instead a random variable (e.g., it depends on unpredictable factors like machine retooling time or an operator’s setup requirements), then each cycle can have a different setup cost K_i. In such a case:
The system still regenerates at production events, but now the total cost in each cycle is K_i + holding cost.
To apply the renewal-reward theorem, we would use the expected setup cost E[K_i] in place of the constant K when deriving the average cost per cycle.
The formula for the long-run cost per unit time would look like ( E[K_i] / (N μ) ) + (some function of h and N).
If K_i has a large variance, there is extra uncertainty. In extreme cases, it might be beneficial to limit the batch size to avoid occasionally incurring extremely large costs in a single cycle—though usually, one still optimizes using the expected value E[K_i].
Pitfall: Relying purely on the expected setup cost might ignore the risk of very large setup costs. In some real-world cases, risk management might favor smaller batch sizes to limit exposure to extremely high costs in any single production run.
How does the solution behave if N is very large or very small in practical terms?
Analyzing extreme values of N:
Very small N: You are constantly setting up production runs for tiny batches. This reduces holding cost because items do not wait long, but the setup cost K is incurred very frequently. The average cost per unit time might rise significantly if K is large relative to h.
Very large N: You set up production less frequently, which reduces the contribution of K on a per-unit-time basis. However, each order that arrives early in the cycle waits potentially a very long time, driving up holding costs.
The optimal N balances these two extremes: it is precisely where the marginal reduction in setup cost matches the marginal increase in holding cost.
Pitfall: In actual systems with a physically limited buffer capacity, extremely large N might not be feasible. Similarly, for extremely small N (like N=1), the system could be overburdened by excessive setups if K is high.
How would you handle a scenario where orders arrive in batches themselves rather than strictly one by one?
If orders arrive in lumps (for example, a single shipment bringing multiple orders at once), the arrival process is no longer a sum of i.i.d. interarrival times for each individual order. Instead, you get a random batch size Y at each arrival, and the interarrival time T might have some mean E[T]. To gather a total of N orders:
You accumulate orders from successive batches until the total in that cycle reaches or exceeds N.
The time to accumulate N orders would be the time until the partial sums of consecutive batch sizes exceed N.
The number of arrivals needed to surpass N is itself a discrete random variable, and the total waiting time can be computed as a sum of T’s associated with each batch arrival.
You still can apply a renewal argument at the time you start production, but the expected cycle length becomes more complicated because it depends on both the distribution of batch sizes Y and the distribution of interarrival times T.
Pitfall: Approximating each batch arrival as multiple single arrivals can lead to inaccuracies. A more direct analysis that accounts for the distribution of the batch size is needed to compute the expected holding time and cost precisely.
How would priority-based scheduling or processing constraints affect this model?
If certain orders have higher priority and must be processed earlier (or have different holding-cost rates), then:
The waiting cost is not simply h j for j total orders; it might be segmented by priority class. Higher-priority orders might incur a higher holding cost rate, or they might have to be processed before lower-priority orders.
You may end up producing smaller batches for high-priority orders immediately, while batching together lower-priority orders. This can violate the simple “accumulate N orders, then run” rule.
The process might still be regenerative at certain events (e.g., when all outstanding orders, of any priority, have been processed), but the cycle cost structure becomes more complex.
Pitfall: Blending multiple priorities in a single “wait for N” approach can be suboptimal if high-priority orders have significantly higher penalty or holding cost. One might need to define different thresholds for different classes of orders or adapt a dynamic scheduling policy.
What if there's a significant lead time for raw materials that must be ordered in advance?
In some production environments, you must order raw materials prior to being able to start production. If the lead time for materials is L, you might want to place the material order once you anticipate you will soon start production for the next batch:
If the lead time L is longer than N μ, then you might have to order materials even before the entire batch of N orders arrives. This adds complexity because you have to forecast the arrival of future orders.
The system might not be perfectly regenerative at the point of finishing production, since the next cycle’s lead time for materials might overlap with the tail end of the previous cycle.
One can still define regeneration points if the production plus material lead time is reset in a cyclical manner, but in practice, the lead time constraint can force a hybrid approach: partial waiting for orders and partial waiting for materials.
Pitfall: Neglecting lead time might lead to idle time or incomplete production runs. In real systems, companies often separate the planning of material inventory from the production batch size to ensure no material shortages occur when it’s time to produce.
What if we need to account for machine availability or downtime?
In some practical scenarios, the machine used for production may break down or require maintenance:
Periodic downtime disrupts the clean cycle analysis. The machine may be unavailable at random times, preventing immediate production even if N orders have arrived.
The renewal-reward theorem can still hold if we define regeneration points at times when production actually finishes and the machine is up again, but the cycle now includes random downtime durations.
The expected cycle length is no longer purely N μ; it also includes the expected downtime. This can inflate the holding cost because orders wait while the machine is repaired or maintained.
Optimization might favor a smaller N if downtime is frequent, to avoid building up a large backlog that sits idle while the machine is down.
Pitfall: Overlooking downtime can lead to underestimating waiting costs in real manufacturing lines with significant machine reliability issues.
What if the arrival process has seasonality or trends?
If arrivals are non-stationary, for example higher rates in peak seasons, then the assumption that each cycle is identically distributed may break down:
During high-demand periods, N orders accumulate faster, so cycle times shorten. During low-demand periods, cycles lengthen.
The average cost per unit time might vary across seasons, making a single optimal N for the entire year suboptimal.
One strategy is to break the year into segments (peak, off-peak) and choose a different N in each segment to match the typical arrival rate in that segment.
Alternatively, you might adopt a dynamic policy that adjusts N adaptively based on observed arrival rates or forecasts.
Pitfall: Using a single N for the entire year when the demand changes drastically across time can lead to large inefficiencies in either the low-demand or high-demand seasons (or both).
How would a real-time control policy differ from the fixed policy of “wait until N orders have arrived”?
In a fixed policy, you commit to starting production exactly when N orders are accumulated. A real-time control policy might evaluate the current state (queue length, time since last production, cost trends) in a continuous manner and decide dynamically when to run production. For instance, it might say:
If the queue length is at least N, start production unless the waiting cost is still less than the expected setup cost reduction from possibly waiting for more orders.
If we are nearing a certain time threshold or if certain orders have become urgent, start production even if the queue length is below N.
This can yield lower costs in complex, non-stationary scenarios or when cost parameters vary with time or queue length. However, analyzing and computing the optimal real-time control policy is usually more complex than the straightforward “batch of size N” approach.
Pitfall: A strictly fixed threshold might be simpler to implement but can be suboptimal in dynamic environments. A real-time approach can adapt better but may require sophisticated software systems and forecasting tools.