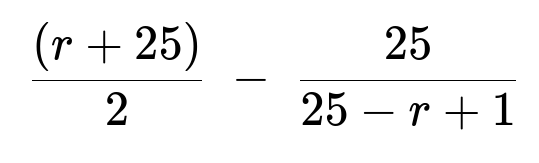ML Interview Q Series: Optimal Stopping Threshold for Maximizing Expected Payoff in a Number Drawing Game
Browse all the Probability Interview Questions here.
Question. You are offered the following game. You can repeatedly pick at random an integer from {1,…,25}. Each pick costs you one dollar. If you decide to stop, you get paid the dollar amount of your last pick. What strategy should you use to maximize your expected net payoff?
Short Compact solution
One optimal strategy is to choose a threshold r (an integer between 1 and 25). You keep drawing until you get a value that is at least r, and then you stop. The expected number of draws needed follows a geometric distribution with success probability (25 − r + 1)/25, so on average you pay 25/(25 − r + 1) dollars in total. The final payoff is uniformly distributed on {r,…,25}, so its expected value is (r + 25)/2. Therefore, the expected net payoff is
Maximizing this with respect to r gives the best threshold r = 19, yielding an expected net payoff of approximately 18.4286 dollars.
Comprehensive Explanation
To analyze this game, consider the following:
Defining the Strategy
We propose a simple threshold-based strategy: pick a number repeatedly and stop as soon as you get a number >= r. This integer r is the decision boundary. If a number is below r, you reject it and pay another dollar to draw again. If it is r or higher, you accept it and receive that number of dollars as your final payout.
Probability of Stopping on a Single Trial
On any single pick, the probability of drawing a number from r up to 25 is (25 − r + 1)/25 because there are 25 − r + 1 integers in {r,…,25}.
Expected Number of Picks
Because each pick is an independent event, the total number of picks until you get a value >= r follows a geometric distribution with success probability p = (25 − r + 1)/25. For a geometric random variable with success probability p, the expected number of trials is 1/p. Hence, here you expect 25 / (25 − r + 1) draws. Each draw costs 1 dollar, so your total expected cost is 25 / (25 − r + 1).
Expected Value of the Payout
If your stopping threshold is r, then whenever you stop, you know the drawn value is in {r,…,25}. In fact, conditional on it being at least r, the value is equally likely to be any integer from r to 25. The expected value of a discrete uniform distribution from r to 25 is (r + 25)/2.
Putting It All Together
Your expected net payoff is the expected final payout minus the expected total cost of all picks. Symbolically:
where
r + 25)/2 is the average of the final chosen number if it is uniformly distributed in {r,…,25}.
25 / (25 − r + 1) is the expected number of times you pay 1 dollar.
Maximizing Over r
The threshold r can range from 1 to 25. We check which r maximizes the above expression. A direct calculation or a quick discrete check from r = 1,…,25 shows that r = 19 gives the largest expected net payoff, which comes out to about 18.4286 dollars.
In more detail, you can check each integer r or use some algebraic manipulation to find a discrete maximum. In practice, since r ranges up to 25, one could just evaluate the expression at each value of r and pick the r that gives the highest number.
Implementation Note
If you wanted to simulate this strategy in Python, you could write a script that tries all r in 1..25, performs a large Monte Carlo simulation for each r, estimates the average net payoff, and checks which r is best. This would be a brute-force approach to confirm your analytical result.
import random
import statistics
def simulate_strategy(r, num_simulations=10_000_00):
payoffs = []
for _ in range(num_simulations):
cost = 0
while True:
cost += 1
x = random.randint(1,25)
if x >= r:
payoffs.append(x - cost)
break
return statistics.mean(payoffs)
best_r = None
best_value = float('-inf')
for r in range(1,26):
val = simulate_strategy(r)
if val > best_value:
best_value = val
best_r = r
print("Best threshold =", best_r, "with approx. net payoff", best_value)
If you run this, you will see the threshold near 19 emerges consistently as the optimal stopping criterion.
Follow-up Question: Could a More Complex Strategy Do Better?
A more complex strategy might consider the exact values you see in each draw. However, because the picking process does not give you any increasing or decreasing probability information and each draw is independent and uniformly distributed, there is no advantage to adjusting your threshold mid-game. A threshold-based strategy that remains the same from the outset is already optimal in this setting.
Follow-up Question: How to Generalize to 1..N?
If you generalize from 1..25 to 1..N, the same reasoning applies:
Let r be the threshold.
The success probability on each draw is (N − r + 1)/N.
Expected cost is N / (N − r + 1).
Expected final draw is (r + N)/2.
Hence the expected net payoff is:
You can optimize this expression over r in {1,…,N}. For large N, you can find a closed-form approximation or just do a discrete search for the best r.
Follow-up Question: What If the Cost per Pick Is Not 1?
If each pick costs c instead of 1, then the expected cost for 25 / (25 − r + 1) draws becomes c * (25 / (25 − r + 1)). The expected net payoff becomes
(r + 25)/2 − c * (25 / (25 − r + 1))
and you again pick r to maximize it. If c is higher, the optimal r might shift in order to avoid drawing too many times.
Follow-up Question: Why a Geometric Distribution?
When you decide to keep drawing until the event “the integer is at least r” occurs, each draw is an independent Bernoulli trial with success probability (25 − r + 1)/25. If you see a success, you stop. The number of trials for the first success in independent Bernoulli trials is geometrically distributed. That is why the expected count of draws is 1/p, and p = (25 − r + 1)/25.
All these considerations confirm that the threshold strategy is optimal under independence and a uniform sampling of integers from 1..25 with constant cost.
Below are additional follow-up questions
What if the distribution of drawn integers is no longer uniform?
If the integers are not drawn uniformly from {1,…,25}, the threshold strategy may still be optimal in a broad class of problems, but the exact threshold would change. Suppose the probability of drawing integer k is p(k) for k in {1,…,25}, where all p(k) sum to 1 but are not necessarily equal.
Expected Number of Draws If you set a threshold r, you stop as soon as you draw a number
>= r. Let S = p(r) + p(r+1) + … + p(25). The expected number of draws in that case is 1/S, because it remains a geometric stopping problem with success probability S. Each draw still costs 1 dollar, so you pay 1/S on average.Expected Payout The expected final payout would be the conditional expectation of the drawn number, given that it is in {r,…,25}. Formally, E(X | X >= r). You can compute E(X | X >= r) as ( r*p(r) + (r+1)p(r+1) + … + 25p(25) ) / S.
Expected Net Payoff The expected net payoff becomes: E(X | X >= r) − (1 / S). You would maximize this expression by searching over r from 1 to 25.
One subtlety is that you may find multiple candidate r values that give nearly the same net payoff, especially if the distribution p(k) has complicated peaks or is heavily skewed. A potential pitfall is assuming uniformity when the real distribution is not. In a real-world scenario, if you mistakenly assume uniform draws, you might end up with a suboptimal threshold.
What if there is a maximum number of draws allowed?
Sometimes, the game could have an upper bound M on how many times you can draw. For instance, if M=10, you cannot keep drawing forever; you have to stop at or before the 10th draw if you never see a number >= r. In this scenario:
Influence on Strategy When there is a maximum of M draws, you must consider the possibility that you could reach the Mth draw without having met your threshold. If that happens, you would be forced to accept whatever the Mth draw is, potentially a low number.
Modified Optimal Stopping The decision might shift to a dynamic one in which your threshold changes as you approach the Mth draw. If you are on the second to last draw, you might accept a smaller number than you would early in the game, because the next (and final) draw is your only remaining chance.
Computational Approach In practice, you can analyze this by backward induction, considering each draw from the last back to the first. You would define a threshold that depends on how many draws remain. This approach is a classic dynamic programming approach:
If you have 1 draw left, you must accept whatever you get.
If you have k draws left, you compare the expected value of stopping now to the expected value of continuing under the threshold strategy for k-1 draws remaining next time.
A key pitfall arises if you assume you can apply the same “static threshold” strategy from the unlimited-draw scenario. Because the maximum number of draws introduces a forced final pick, your threshold would optimally vary with the number of draws left.
What if the cost per draw changes over time?
In real-world settings, sometimes each draw may have a different cost. For example, the cost might be 1 dollar for the first 5 draws, then 2 dollars thereafter, or it might progressively increase with each draw.
Impact on Expected Cost The expected cost is no longer simply (cost per draw) times (expected number of draws). You might pay 1 dollar for each draw up to a certain point, then 2 dollars for draws after that.
Optimal Strategy Alteration If the cost after the 5th draw doubles, you might be more conservative in your threshold choice from the start, because each additional draw becomes significantly more expensive.
Complexity and Dynamic Threshold This can lead to a dynamic threshold that changes once you cross the boundary where the cost spikes. Initially, you might wait for a higher threshold, but after the cost jumps, it may become beneficial to accept a lower payout rather than pay the higher cost.
A subtle pitfall is to treat the cost as a fixed 1 dollar per draw and ignore the rising cost. That could severely reduce your net payoff if, in reality, repeated draws become increasingly expensive.
How does risk aversion alter the strategy?
Everything so far assumes you are maximizing expected value (risk-neutral). But if you are risk-averse, you may place additional value on securing a moderately high number quickly rather than risking many draws to chase a possibly higher number.
Utility Function Instead of maximizing the simple expected monetary payoff, you might maximize E(U(X − cost)), where U(·) is a concave utility function (for instance, U(x) = log(x)).
Effect on Threshold A risk-averse utility typically leads to more conservative behavior, meaning a lower threshold. You would be more inclined to stop earlier to avoid repeated draws and the associated risk of higher cost.
Computational or Analytical Complexity Finding a closed-form solution might be more involved because the distribution of outcomes and costs must be mapped through the utility function. Nonetheless, a search-based approach over r in {1,…,25} is still feasible for modest ranges.
A potential pitfall here is ignoring psychological or utility-based considerations in real-world scenarios, where a purely risk-neutral approach may not capture the decision maker’s true preferences.
What if you can observe the outcomes of previous draws and the game allows a second chance?
In a variant scenario, you might see the entire history of draws. Perhaps you have the option: once you skip a number, you can draw again (as usual), but there could be a one-time opportunity to recall a previous number if you regret skipping it.
Memory and Recalling If you can recall a past draw only once, you must decide whether to claim that past draw or continue to draw for something better.
Strategy Complexity This is no longer a straightforward geometric problem. You have to track whether you used your recall option or not, and which number you plan to recall. You also have to decide how many future draws you are willing to pay for to improve upon that recalled number.
State-Based Dynamic Programming You could define your state as: (current draw number, best previously seen number, whether recall is still available). Then you can formulate the value function for continuing or stopping. Because the cost accumulates with each draw, you weigh the expected gain from future draws with the possibility of recalling the best past outcome.
A subtle pitfall is underestimating how quickly the cost can build up while waiting for an improved number. Even if you have a recall option, repeated draws might not be worth the extra cost if the odds of finding a significantly better number are low.
What if the game ends immediately when you draw a 25?
Imagine a variant rule: if you ever draw the maximum possible number (25), you must immediately stop and take that number. Does this affect the threshold strategy?
Forced Stopping at 25 This new rule forces an immediate stop if you draw a 25, so you no longer have the freedom to continue paying for draws hoping for a particular threshold. In practice, this usually benefits you because 25 is the highest possible draw.
Strategy Impact If 25 triggers an automatic stop, you might slightly adjust your threshold for numbers less than 25. Suppose you are considering r=19. Under the standard game, drawing a 19 or higher triggers a stop. But now, if you see 25, you are forced to stop anyway. Because 25 is a guaranteed best outcome, you may not lose out. However, if you are risk-averse or if the distribution is skewed, it can still shift your optimal threshold.
Expected Value Computation The expected net payoff changes slightly if forced stopping on 25 is an additional event. However, in the original uniform scenario, drawing 25 is still a “success” that is at least r. So in the simple threshold strategy, forced or voluntary, it amounts to the same outcome. The difference emerges if the distribution is not uniform or the cost structure is more nuanced.
One subtle pitfall is that some might believe a forced stop at 25 heavily changes the analysis. But in a uniform setting with cost = 1 per draw, once you adopt a threshold r <= 25, drawing a 25 is already your best scenario, so you would have stopped anyway. Hence, the effect might be smaller than expected unless there are additional complexities.