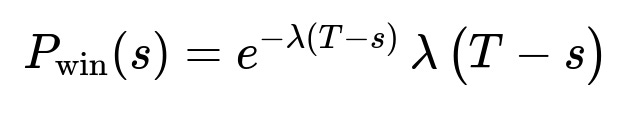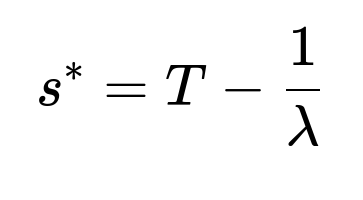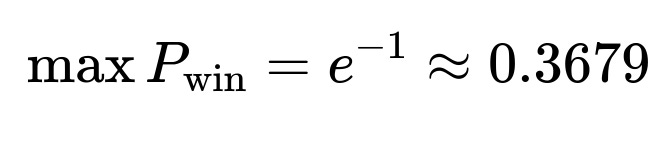ML Interview Q Series: Optimal Waiting Strategy for Capturing the Final Poisson Process Signal.
Browse all the Probability Interview Questions here.
In a video game with a time slot of fixed length T, signals are generated according to a Poisson process with rate λ, where T > 1/λ. You are allowed to push a button only once during [0, T]. You win if at least one signal occurs in [0, T], and you push the button exactly at the occurrence of the last signal. Your strategy is to wait a fixed time s (with 0 < s < T) and then push the button at the first signal that occurs (if any) after time s. What is your probability of winning the game, and what value of s maximizes this probability?
Short Compact solution
The probability of winning can be seen as the probability of having exactly one signal in (s, T). By the memoryless property of the Poisson process, this probability becomes e^(-λ(T−s)) * λ(T−s). Taking the derivative of this expression with respect to s and setting it to zero gives the optimal time s = T - 1/λ. The resulting maximal probability is e^(-1) ≈ 0.3679, independent of T and λ (as long as T > 1/λ).
Comprehensive Explanation
Underlying Reasoning
In a Poisson process with rate λ, the times between consecutive signals are independent and exponentially distributed with parameter λ. The memoryless property tells us that if we wait until some time s and no signal has arrived, the subsequent waiting time for the next signal behaves exactly as it did from time 0. This allows us to write the probability of winning purely in terms of the interval (s, T).
Formulating the Probability of Winning
You win exactly when there is exactly one signal in the time interval (s, T). That is because if there is more than one signal in (s, T), then you would be forced to push the button at the first occurrence within that interval—hence not pushing it at the last signal. Meanwhile, if there are zero signals in (s, T), you do not get to push at all.
The probability of seeing exactly one signal in (s, T) for a Poisson(λ) process with length (T - s) is:
Here:
λ is the rate of the Poisson process.
(T - s) is the length of the interval from s to T.
The factor e^(-λ(T−s)) is the probability that zero signals occur in (T - s).
Multiplying by λ(T - s) gives the probability that exactly one signal occurs in that interval.
Finding the Optimal s
We want to find the value of s that maximizes P_win(s). Conceptually, if we set s too early, we risk the possibility that multiple signals will occur after s. If we set s too late, we reduce the probability of getting any signal at all after time s.
Mathematically, we take the derivative of P_win(s) with respect to s, set it to zero, and solve for s. This yields:
Maximum Probability
By substituting s* = T - 1/λ back into P_win(s), we obtain the maximum probability. One can recognize that this corresponds to the maximum of the function x e^(-x), which is attained at x=1, giving:
This value is independent of λ and T, provided T > 1/λ, so that s* remains within the interval (0, T).
Follow-up Questions
Could you explain the memoryless property in more detail?
The memoryless property for an exponential waiting time (rate λ) means that if no signal has arrived by time s, the waiting time from s onward does not depend on how long we have already waited. In simpler terms, if X is an exponentially distributed random variable with parameter λ, then:
P(X > s + t | X > s) = P(X > t).
In the context of a Poisson process, once we condition on the event that no signal arrived before time s, the process “restarts,” and times to subsequent signals have the same exponential distribution. This property underpins the probability calculation for exactly one signal occurring in (s, T).
What happens if T ≤ 1/λ?
Our solution for s* = T - 1/λ relies on T being greater than 1/λ. If T ≤ 1/λ, then T - 1/λ would be non-positive, which would not be a valid choice of s inside the interval (0, T). In such a scenario, you cannot use that formula. Instead, the maximum might occur at a boundary (e.g., s close to zero) or might need re-derivation by directly analyzing P_win(s) in the restricted domain.
What if no signals occur during [0, T]?
If no signals occur in [0, T], then you do not get to press the button in time. Thus, you automatically lose in that scenario. This possibility is accounted for in the probability calculation because P_win(s) explicitly assumes exactly one signal in (s, T). When zero signals occur in (s, T), that portion of the probability does not contribute to your winning outcome.
Could you elaborate on the connection between the Poisson distribution and exponential waiting times?
A Poisson process with rate λ has inter-arrival times that are exponentially distributed with parameter λ. Specifically, the number of arrivals in any interval of length τ follows a Poisson(λτ) distribution. Equivalently, the time between arrivals follows Exp(λ). The memoryless property of the exponential distribution is key in computations involving “waiting for the next arrival” after some time has elapsed without arrivals.
How can I verify that the probability e^(-1) does not exceed 1?
Observe that e^(-1) is roughly 0.3679, which is certainly less than 1. Mathematically, e^(-1) = 1/e, and e is about 2.71828, making 1/e around 0.3679. This fits within the valid range of probabilities.
Could you provide a quick Python snippet to calculate this probability numerically?
Below is a short example using Python for different values of s. We assume λ = 2.0, T = 2.0 (which is > 1/λ = 0.5). We scan s in (0, T) and pick the maximum:
import numpy as np
lambda_rate = 2.0
T = 2.0
s_values = np.linspace(0, T, 1000)
def p_win(s, lam, T):
return np.exp(-lam * (T - s)) * lam * (T - s)
prob_values = [p_win(s, lambda_rate, T) for s in s_values]
max_prob = max(prob_values)
opt_s = s_values[np.argmax(prob_values)]
print("Max Probability:", max_prob)
print("Optimal s:", opt_s)
You would see that opt_s is close to T - 1/lambda_rate = 2.0 - 0.5 = 1.5, and max_prob is close to e^(-1) ≈ 0.3679.
By understanding these points, one can see how the core principle—the memoryless property of the exponential distribution—enables us to derive a simple but elegant solution to find both the winning probability and the optimal strategy for choosing s.
Below are additional follow-up questions
What if there is a small reaction delay when pressing the button?
A real-world consideration might be that you cannot push the button exactly at the signal time, but instead there is a reaction delay d (a small positive constant). In other words, if the signal arrives at time t, you actually press the button at time t + d. Would this affect the optimal strategy or the probability?
Detailed Answer
Impact on the winning condition The winning condition says you must push the button at the arrival of the last signal. If you have a reaction delay, then even if a signal arrives at time t, your press is effectively at time t + d. This may invalidate the condition of pressing “exactly at” the last signal arrival time, since you would no longer coincide with the signal time.
Possible ways to model
Strict interpretation: The reaction delay means it is impossible to press exactly at a signal. You cannot win under the original rules if the last signal arrives after time s.
Relaxed interpretation: You can still “claim” the push if your press occurs within an acceptable small interval around the signal time (e.g., if t + d is “close enough” to t that the game treats it as a successful immediate push).
Adjusting the strategy
If the strict interpretation is used, the entire approach for maximizing e^(-λ(T−s)) λ(T−s) becomes moot, because the last signal in (s, T) cannot be matched precisely. One might then need to shift the time s earlier to compensate for d, in the hope that by the time you react, it aligns with the signal occurrence.
If the relaxed interpretation is used, the problem might remain effectively the same if the permissible pressing window is short and automatically accounted for.
Conclusion In a truly strict scenario, even a small reaction delay prevents you from ever pushing at the exact signal time. You would need to redefine the winning condition in a more realistic manner (e.g., pressing within a short window of the last signal). Once redefined, you could re-derive an optimal s by replacing the notion of “exact time of signal” with “within d of the signal” and carefully computing the adjusted probability.
How would the strategy change if the process has a random or partially known rate λ?
In some cases, λ is not fixed but rather drawn from a distribution, or you only have an estimate of λ from past observations. How do you incorporate uncertainty about λ into the strategy?
Detailed Answer
Bayesian perspective Suppose you have a prior distribution for λ, for example a Gamma distribution, which is conjugate to the Poisson likelihood. As signals are observed over time in different game rounds, you update this prior to a posterior distribution over λ.
Expected utility approach Instead of a single P_win(s) = e^(-λ(T−s)) λ(T−s), you would consider the expected probability of winning with respect to the posterior distribution of λ. Formally, you would compute the integral:
P_win(s) = ∫ [ e^(-λ(T−s)) λ(T−s) ] p(λ) dλ
where p(λ) is your posterior density for λ.
Optimal s To find the best s, you would then differentiate this integral with respect to s, set it to zero, and solve. The resulting s might no longer be T - 1/λ but will instead depend on the mean or other moments of the posterior.
Practical pitfalls
If the posterior for λ is wide (high uncertainty), the maximum may shift away from T - 1/E[λ].
A numerical optimization approach might be necessary if no closed-form solution exists.
Could the presence of multiple signals arriving simultaneously affect the outcome?
In theory, a Poisson process does not generally produce simultaneous signals with probability > 0, since the exponential inter-arrival times are continuous. However, in discrete approximations (for instance, a computer game might have discrete time steps), collisions of multiple signals at the exact same time could occur.
Detailed Answer
Ideal continuous-time Poisson process The probability of two signals arriving exactly at the same instant is zero. Hence, the phenomenon “simultaneous arrivals” is a measure-zero event in continuous time.
Discrete-time approximation or computational rounding In a computer simulation or game engine, if time is advanced in small steps (e.g., 1 millisecond increments), it is possible for more than one arrival to fall into the same discrete time bin.
Impact on game logic
The game might treat them as separate signals at times t and t+ε, where ε is extremely small.
Alternatively, if the game lumps them together as a single event at time t, you effectively see one arrival with a “multiplicity” of two signals. This can matter if “last signal” means the last actual Poisson arrival or the last discrete-time event.
Mitigation
You can design the system to break ties by randomizing the signals across the discrete interval.
If collisions do occur and are recognized by the engine, you might need additional rules on how to interpret “pushing the button at the last signal.” For instance, you could define that if multiple signals arrive in the same discrete time step, the last signal among them is effectively the same time as the first.
Conclusion In continuous mathematics, no change. In real-world or discretized contexts, consider collision resolution carefully, as it can alter the exact probability outcomes slightly.
What if you only observe partial information about signal arrivals before time s?
Consider a scenario where signals that arrive before time s might or might not be visible to you. For instance, you do not have access to whether any signal arrived in (0, s), but you only start observing signals after s. Could this change the reasoning behind your strategy?
Detailed Answer
Standard assumption The classic result that the optimal s is T - 1/λ relies on full knowledge of no signals in (0, s). This is part of the memoryless property: if no arrival is seen by s, then from that point forward, your distribution for the waiting time to the next arrival resets.
Partial observability
If you do not know whether signals arrived in (0, s), you cannot be certain the process is “resetting.” In fact, signals might have arrived but remain hidden.
The memoryless property in a Poisson process specifically pertains to the waiting time from s given that no signal has arrived before s. If that condition cannot be confirmed, your waiting distribution from s onward might differ.
Potential effect on the strategy
If there is still a high chance that multiple signals could already have occurred by s, then the “last signal” might have already passed. That invalidates the strategy of waiting for the first signal after s.
Alternatively, if you have some partial or probabilistic knowledge about signals before s, you might form a Bayesian belief about how many signals occurred before s. This belief informs how likely you are to still see more signals after s.
Conclusion Full visibility of arrivals up to s is crucial to the memoryless argument. With partial visibility, you would need a more involved model that incorporates your uncertainty about how many signals already occurred before time s.
How would you verify the distribution assumption in practice?
The entire approach hinges on having a Poisson process. In real applications (like server requests, sensor events), the process might deviate from Poisson. How do you check that assumption before applying this strategy?
Detailed Answer
Empirical checking
Inter-arrival time distribution: Collect arrival times, compute inter-arrival durations, and check whether they appear exponentially distributed (e.g., via a Q–Q plot or a Kolmogorov–Smirnov test).
Variance-to-mean ratio: In a Poisson process, the sample variance of the count in fixed intervals should be equal to the sample mean.
Potential deviations
Overdispersion: If the data exhibit more variance than expected, you might be dealing with a process that is not memoryless (e.g., a renewal process with a heavier tail).
Time-varying rate: If λ is not constant but changes over time, the process is inhomogeneous, and the memoryless property no longer holds.
Implications
A mismatch can invalidate the formula e^(-λ(T−s)) λ(T−s).
You must adjust your strategy to account for the actual arrival distribution, possibly adopting a time-dependent rate model or a more complex counting process.
Could the game end prematurely or extend beyond time T?
In certain real scenarios (e.g., server-based simulations or partial system failures), the “time slot” might unexpectedly terminate before T or might be extended beyond T. Does this possibility affect the optimal s or the probability?
Detailed Answer
Premature termination
If the game can end at a random time < T, then you face a risk: waiting too close to T might mean you never get to push the button if the game ends early.
You might model the game’s actual end time as a random variable E, and you only have from 0 to min(T, E). Maximizing your probability could shift your strategy to push earlier, reducing the chance of being forced out by an early end.
Extension beyond T
If T can become T’> T, but you did not know that in advance, you might inadvertently push the button “too early.” If you had known T was extended, you might wait longer to keep the single-arrival probability in a bigger window.
This typically suggests that your strategy must be adaptive to changes in the environment, rather than a fixed s.
Practical approach
If the potential for termination or extension is large, building a dynamic or real-time response strategy (e.g., continuous re-optimization based on updated knowledge) may outperform a fixed cutoff s.
Could the button be used more than once if signals are rare?
Sometimes real games might say “You can press the button only once,” but there is a possibility of recharging or unlocking a second press if signals are not seen for a while. Would a second press opportunity change the analysis?
Detailed Answer
Single-press assumption
The entire derivation P_win(s) = e^(-λ(T−s)) λ(T−s) hinges on the fact that you only get one shot. Multiple presses would allow you to attempt a second time if the first press fails.
Two-press extension
If you had two presses, you might want to press early to catch a potential last signal and still save a press for a new “last signal” if more appear.
However, you do not know how many signals will occur or when. The problem becomes significantly more complex—potentially requiring dynamic programming or Markov decision processes to handle the state of how many signals arrived so far and how many presses remain.
Benefit
Generally, multiple button presses can only increase your overall probability of winning. The single-press optimal strategy is not necessarily the global optimum when you can press multiple times.
Conclusion A multi-press scenario invalidates the single-step memoryless argument because your decision at time s must also consider whether a subsequent signal might appear in (s, T). The solution might then require a more advanced approach to account for multiple potential press times.
How does this strategy hold up if λ depends on external conditions within the time slot?
In many real-world contexts, arrival rates can depend on time or external conditions (e.g., bursts of traffic at certain times). We assumed a homogeneous Poisson process with constant λ. What if λ(t) changes over [0, T]?
Detailed Answer
Non-homogeneous Poisson process If λ = λ(t) is time-dependent, the time between arrivals is no longer memoryless, and the distribution of arrivals in (s, T) is determined by integrating λ(t) over that interval.
The expected number of arrivals in (s, T) becomes ∫ from s to T of λ(u) du.
The probability of exactly one arrival in (s, T) is e^(-Λ(s, T)) * Λ(s, T), where Λ(s, T) is the integral ∫ from s to T of λ(u) du only if it still behaves like a Poisson process. The memoryless property, however, is lost, so you cannot simply say it restarts at s in the same manner.
Optimal s
You would need to compute the probability that exactly one signal arrives after s, given no arrivals have occurred by s. This becomes more complicated because the chance of having no arrivals in (0, s) depends on ∫ from 0 to s of λ(u) du, and the conditional distribution from s to T depends on λ(t).
Typically, you solve it numerically by formulating the function:
P_win(s) = Probability{exactly 1 arrival in (s, T) | 0 arrivals in (0, s)}
Then, differentiate and find the maximum over 0 < s < T.
Practical pitfalls
If λ(t) spikes near the end, you might want to set s near that spike to capture a single signal.
If λ(t) is very high in the beginning and then drops, you might want to push earlier.
Conclusion The uniform rate solution (s* = T - 1/λ) no longer applies. You must incorporate the time-varying function λ(t) into the analysis, typically via direct integrals or numeric simulation.
How can numerical simulation confirm the theoretical results?
Even when you have a closed-form solution for s and the probability, it is good practice to run a Monte Carlo simulation. How can you design such a simulation to validate the expression e^(-λ(T−s)) λ(T−s) and the optimal strategy?
Detailed Answer
Outline of the simulation
Parameter setup: Choose λ, T, and a candidate s.
Generate arrivals: For each simulation run, simulate a Poisson process over [0, T]. This can be done by repeatedly sampling inter-arrival times from an Exp(λ) distribution until the sum of arrivals exceeds T.
Apply strategy: Check if a signal arrives in (s, T). If one does, identify the first arrival time in (s, T). Determine if that arrival is also the last among all arrivals in [0, T].
Record success/failure: Tally how often you succeed (i.e., the button press is at the last signal in [0, T]).
Compute empirical probability: Divide the number of successes by the total runs to estimate P_win(s).
Validation
Repeat for a fine grid of s values in (0, T). Identify the s that yields the highest empirical P_win(s).
Compare to the theoretical s* = T - 1/λ, and see if the empirical probability of winning is near e^(-1).
Edge cases
If T is too small or close to 1/λ, you may see boundary effects.
If λ is extremely large or extremely small, you might need a large number of simulation runs to accurately estimate the probabilities.
Conclusion Simulation can provide evidence that the analytic solution is correct. It helps reveal any numerical or real-world complexities that might invalidate ideal assumptions (like memorylessness or continuous time).
What if the game requires at least two signals before you can press the button?
Imagine a rule variation: you must wait for at least two signals to occur somewhere in [0, T], and only after the second signal can you decide to press the button at some subsequent signal. How does this change the problem?
Detailed Answer
Modified rules
Now, you cannot press on the very first signal that appears, even if it is after time s. You must allow at least two signals to occur. After the second signal, you get one chance to push the button at the next signal.
Alternatively, you could interpret it as a fixed time s, but you are only allowed to press if at least two have already arrived by s. The exact framing matters a lot here.
Loss of simple memoryless property The event “two signals have occurred by time s” changes the conditioning. Once two signals have appeared, the next waiting time for the third signal is still exponential, but your initial waiting times for the first two signals complicate your knowledge of how much time remains in [0, T].
Potential approach
Model the arrival times of the first and second signals.
Condition on these times to see how much of the interval remains and whether more signals will come.
Decide if and when to push the button to maximize the chance that it coincides with the final arrival in [0, T].
Added complexity The probability that exactly one signal arrives after the second signal can no longer be neatly expressed as e^(-λ(T−s)) λ(T−s), because you first need the distribution of the time the second signal arrives. This typically leads to a more involved integral or a piecewise approach.
Conclusion The single-press, single-signal scenario is elegantly solvable with memorylessness. Requiring two or more signals prior to pushing breaks the neat structure and generally necessitates more advanced probabilistic or computational techniques (such as enumerating the distribution of arrival times for multiple signals, or using Markov chain models).
What if T is extremely large, and you can only stay in the game up to a certain finite time before you must leave?
Sometimes T can be very large, but you physically can only remain at your station until some time L < T. You must either press by L or forfeit. Does this alter the optimal approach?
Detailed Answer
Truncation at L
You effectively have a new time window [0, L], even if the official game window is [0, T] with T > L. You are forced to leave after L, so you cannot observe or press at signals beyond L.
This means you can only push during (s, L) rather than (s, T).
Revised problem
The probability of a successful press then depends on the chance that no signals arrive in (s, L) before the first signal after s, and that this signal is also the last arrival in [0, T]. But you cannot witness signals after L.
If signals do occur after L, you cannot be present to press at them, so you effectively lose.
Heuristic
If L < T - 1/λ, the original solution s* = T - 1/λ is not feasible. You might place s near L - 1/λ, but that still assumes you can measure the entire final outcome in [L, T].
A more direct analysis would see how likely it is that any signals appear in (L, T). If that probability is high, pressing any signal before L might not align with the final signal of the entire interval [0, T].
Conclusion In real-world usage, if you cannot remain for the entire interval, your winning probability is reduced. The standard formula does not apply. You would need to incorporate the probability that no signals arrive in (L, T), given what happened in [0, L], to refine your strategy.
What if pressing the button slightly shortens the time window T?
In certain game mechanics, pressing the button might cause the time slot to end immediately or reduce the remaining time for further signals. This effectively changes the distribution of future arrivals.
Detailed Answer
Immediate termination If pressing the button ends the time window at once, you cannot have additional signals beyond that press. So to win at the last signal, you want to ensure no further signals would have arrived had the time continued. But in practice, the game terminates, so “last signal” becomes the final signal for that truncated timeline.
Shortening T If pressing at time t sets T to t + Δ (some small leftover portion) or something similar, then the future arrivals are restricted to at most Δ time.
Strategy implication
The probability that your pressed signal is the final one depends on how probable it is that no signals appear in the truncated interval.
A naive approach might be to wait until near T, press on the next arrival, and end the game. But if pressing earlier can manipulate T in a beneficial way (e.g., if you force the game to end before further arrivals can appear), that might be advantageous.
Analysis This problem no longer matches the standard Poisson arrival scenario without intervention. You must incorporate the effect of how your press modifies T. Typically, that leads to a dynamic approach: at each moment, weigh the probability of future arrivals versus the benefit of ending the time slot now.
Conclusion Once pressing the button changes the timeline, you disrupt the normal memoryless environment. A specialized model is needed to precisely calculate the resulting probabilities.
How does the solution hold up if you change the criterion to “the last signal in a window that starts when you press and ends at T”?
Imagine flipping the perspective: you push the button at time s, and from that point onward, you can only win if exactly one signal arrives after s (including s itself if a signal arrives at s). Does that reinterpretation coincide with or differ from the original question?
Detailed Answer
Original question The original states you wait until s, then you push on the first signal that arrives after s. That signal must be the last in [0, T].
Alternative framing If “last signal” is redefined to be the last in [s, T], then memorylessness might make it simpler: The probability that exactly one signal arrives in (s, T) is e^(-λ(T−s)) λ(T−s).
Differences
In the original problem, signals in (0, s) do not directly reduce your chance of winning, but they can matter for whether the signal you press is truly the final one overall.
In the new framing, we only care about signals in (s, T). The notion “last signal in [s, T]” can be simpler or more complicated depending on how the game is set up.
Result If the question literally is “Press at s, then among (s, T), exactly one signal arrives,” you get the same probability expression for “one signal in (s, T)”—but the timing of the press is now locked at s instead of upon the arrival of the first signal after s. That difference changes the mechanics of how you detect the arrival.
Conclusion While it might look similar, the moment of pressing relative to the arrival can differ. Clarifying these small details in the rules can significantly alter the probability model.
If signals occur rarely, can we approximate the probability that you get no signals at all, and how it factors into the winning chance?
In practice, if λ is small and T is moderate, the probability that zero signals occur in [0, T] might be significant. How do you account for that in your strategy or final probability?
Detailed Answer
Zero-signal scenario
If no signals occur in [0, T], you automatically lose, because you never press at a signal.
The probability of zero signals in [0, T] is e^(-λT).
Effect on the one-signal calculation
P_win(s) = e^(-λ(T−s)) λ(T−s) is the conditional probability that exactly one signal occurs in (s, T) given that you wait to press. You still need that at least one signal is in [0, T].
The overall chance of seeing at least one signal in [0, T] is 1 - e^(-λT).
Strategy is unaffected
Even if zero signals are likely, the memoryless property ensures that your best time s is still T - 1/λ to maximize the chance that only one arrives in (s, T).
However, if you want to factor in the possibility that zero signals appear, you might say the unconditional probability of winning is (1 - e^(-λT)) times the conditional probability that the single signal in (s, T) is the last. But that same factor 1 - e^(-λT) does not change which s maximizes the conditional probability.
Conclusion While the zero-signal scenario can be a large chunk of the outcome space for small λ, the memoryless aspect of the process still yields T - 1/λ as the best s. The main difference is that your overall success probability might be smaller in absolute terms because you often see zero arrivals in [0, T].