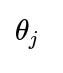ML Interview Q Series: Parametric vs Non-Parametric Machine Learning: Understanding and Choosing the Right Model.

📚 Browse the full ML Interview series here.

Parametric vs Non-Parametric Models: What is the difference between a parametric and a non-parametric machine learning model? Give an example of each (for instance, logistic regression vs. k-nearest neighbors) and discuss in what situations you might prefer a non-parametric approach despite it potentially needing more data to generalize well.

Understanding Parametric Models

A parametric model assumes a specific functional form with a fixed number of parameters. Even as you add more training data, the number of parameters remains constant or grows in a manner that does not strictly depend on the size of the data. Logistic regression is a classic example. Its hypothesis can often be written as a specific function mapping inputs to outputs. In logistic regression, you optimize parameters such that you minimize a loss function measuring how well your model’s predicted probabilities match the actual class labels. Because the model form is specified in advance, you have fewer parameters to learn, which usually requires less data to train reliably and often leads to faster training times. However, parametric models can be more prone to underfitting if your assumptions are not suitable for the complexity of the task.

Understanding Non-Parametric Models

A non-parametric model does not make strong assumptions about the form of the mapping function. Instead, it can grow in complexity as more data is made available. k-Nearest Neighbors (kNN) is a prototypical non-parametric model. At training time, kNN essentially stores the data rather than fitting a compact set of parameters. At inference time, it looks at the k closest training examples to decide on a label or regression output. The capacity of such models can increase with the amount of training data, allowing them to capture more complex decision boundaries and nuances in the input space. However, non-parametric models typically require more data and are computationally more expensive at inference. They also risk overfitting if not carefully tuned (for example, choosing an appropriate k).

Preference for Non-Parametric Approaches

One might still prefer non-parametric approaches in settings where the data distribution is complicated and not well-modeled by common parametric functions. When you lack a priori knowledge about the functional relationship between features and labels, non-parametric models can adapt more flexibly. Though they may need more data to realize this advantage, they often capture local patterns effectively. Hence, for tasks involving highly complex or irregular data distributions, or for scenarios where you can leverage large datasets, non-parametric models can sometimes offer strong performance without explicitly choosing a functional form.

Detailed Mathematical Viewpoint

You often see parametric models expressed in terms of a set of parameters that do not grow with the data size. In logistic regression, the hypothesis might take the form:

where the parameters are contained in

θ

and the input vector is

x

. No matter how large your training set is, you only learn a fixed-size

θ

(assuming a fixed number of features).

In contrast, a non-parametric model like kNN does not have a fixed parameter representation of the data. At prediction time, you find the k nearest neighbors among the stored training data. If your training set grows in size, you essentially keep a larger dataset of examples, which is part of the model itself. The model can adapt its boundary more fluidly but also becomes more computationally heavy during inference.

Possible Code Example

Below is a simple Python illustration of a parametric (logistic regression) vs non-parametric (kNN) classifier using scikit-learn:

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score

# Generate synthetic binary classification data
X, y = make_classification(n_samples=1000, n_features=10, random_state=42)

# Split into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Parametric model: Logistic Regression
lr_model = LogisticRegression()
lr_model.fit(X_train, y_train)
lr_preds = lr_model.predict(X_test)
lr_acc = accuracy_score(y_test, lr_preds)

# Non-parametric model: k-Nearest Neighbors
knn_model = KNeighborsClassifier(n_neighbors=5)
knn_model.fit(X_train, y_train)
knn_preds = knn_model.predict(X_test)
knn_acc = accuracy_score(y_test, knn_preds)

print("Logistic Regression Accuracy:", lr_acc)
print("kNN Accuracy:", knn_acc)

Both models can perform adequately, but they differ in terms of computational cost, how they adapt to complex boundaries, and how they scale with data.

Challenges and Considerations

One challenge with parametric models is model underfitting if the chosen functional form is too simple. For non-parametric models, a frequent concern is computational complexity as the dataset grows, since predictions often require a search among more data points. Another concern is that non-parametric methods can overfit if you pick hyperparameters poorly (like choosing too few neighbors in kNN). However, if your dataset is sufficiently large and you carefully tune your hyperparameters (such as k in kNN), a non-parametric approach can often capture complex patterns without explicit assumptions.

What happens when you have a very large number of features in a non-parametric model like kNN?

When you have a high-dimensional feature space, distance-based methods can suffer from the curse of dimensionality. In high-dimensional spaces, the concept of “distance” becomes less meaningful because points tend to appear equally far from one another. This issue can degrade the performance of kNN, leading to a need for dimensionality reduction or feature engineering. Another potential fix is to move away from purely distance-based approaches and leverage methods that can learn an appropriate representation of the data. For instance, if the feature space is extremely large, you might consider using techniques like principal component analysis (PCA) or autoencoders to reduce dimensionality before applying kNN.

How would you mitigate overfitting in a non-parametric method such as kNN?

You would typically start with tuning hyperparameters, especially the value of k. A higher value of k usually smooths out the decision boundary and reduces variance, which mitigates overfitting. You might also consider distance weighting, where closer neighbors are given more weight than farther neighbors, or applying cross-validation to systematically find optimal hyperparameters. Additionally, employing dimensionality reduction can remove noisy features and help reduce overfitting.

Could you discuss strategies to make parametric models more flexible without fully going non-parametric?

You can often increase the complexity of a parametric model by enriching its hypothesis class. For example, you could use polynomial features in logistic regression or neural networks with more layers or more neurons per layer. Techniques such as regularization help control overfitting while still allowing these models to learn more complex decision boundaries. In practice, deep neural networks are an example of a parametric approach with extremely high capacity, bridging some of the gap between purely parametric and purely non-parametric models. Even though the number of parameters may become very large, it is still generally independent of the size of the dataset.

Why might a non-parametric model be preferred for complex time-series data?

Time-series data often contain nonlinear dynamics, seasonality, and local correlations that might not be well-captured by a simple parametric form. A non-parametric approach can adapt on the fly to local patterns without constraining itself to a rigid functional template. For example, using a kernel-based approach or a nearest-neighbor-based approach can capture local structure more effectively than making an assumption like linear dependence or fixed exponential decay. However, data collection volume, efficiency at inference time, and potential noise in real-world time-series must be addressed to prevent overfitting.

What are practical concerns about using non-parametric models in resource-constrained environments?

Non-parametric models can require storing and scanning through large datasets during inference. In real-time settings or resource-constrained devices, such overhead can be a limiting factor. If you have billions of data points, kNN becomes infeasible without specialized data structures like KD-trees, Ball Trees, or approximate nearest neighbor search. Even with those optimizations, you have to be mindful of available memory, inference latency, and energy costs. A parametric model might be more suitable in embedded systems or edge devices where inference time must be extremely fast.

Could you give an example of a hybrid approach?

One hybrid approach is to train a parametric model on top of non-parametric outputs. For instance, you might generate local features from a non-parametric method and feed them into a neural network or logistic regression. Another approach is to store training data in memory, use a technique like kNN for a coarse classification or regression, and then apply a parametric model locally for refinement. Such strategies aim to get the best of both worlds: the flexibility of non-parametric methods and the compactness and speed of parametric methods.

---

Below are additional follow-up questions

How do parametric and non-parametric models handle missing data, and are there special considerations for each approach?

Missing data is a widespread challenge in real-world machine learning scenarios. In a parametric model such as logistic regression or linear regression, missing data is typically handled via imputation, dropping rows (if feasible), or leveraging techniques like maximum likelihood estimation. Parametric models often rely on a well-defined feature vector for each data point, so if features are missing, the model’s mathematical formulations can break down unless you carefully handle those missing values. For instance, if you are using a standard logistic regression with a feature vector

x

, the expression

becomes incomplete if some components of

x

are missing, so imputation or a specialized missing-data strategy is required.

Non-parametric models like k-Nearest Neighbors can also be sensitive to missing data, especially if distance calculations are used directly for neighborhood determination. When a data point has missing features, the distance metric can be undefined, or severely skewed if you simply treat missing values as zero. In practice, you may need specialized distance metrics that ignore or weight missing features differently. Alternatively, you might impute missing features before running kNN, but if your data has a lot of missing values, your imputation approach can drastically affect the performance. A subtle pitfall is that while kNN might handle partially missing data by ignoring certain dimensions in distance calculations, it can lead to biased neighborhood selections if missingness is not random.

Another subtlety is the correlation between missingness and specific outcomes. If the pattern of missing data itself contains information (for instance, patients who miss a particular test may be systematically different from those who don’t), you may want to introduce an additional binary feature indicating whether that data point is missing a particular value. Parametric models handle this extra feature in a straightforward way (it just becomes another parameter in

θ

), while in non-parametric methods, you have to define how this extra binary feature interacts with your distance measure. In real-world data, it’s often wise to test multiple imputation strategies and see which best suits the modeling approach chosen.

How do these model classes typically deal with outliers, and which might be more robust in the presence of significant outliers?

Parametric models vary in their robustness to outliers. A linear regression model trained with ordinary least squares, for example, is notoriously sensitive to outliers because the objective function squares the residuals, making large errors especially penalizing and shifting the model parameters significantly. Techniques such as robust regression (using a different loss function like Huber loss or absolute deviation) can mitigate this issue by reducing the influence of extreme residuals.

Logistic regression, being a classification model with a log-likelihood objective, can sometimes be less dramatically impacted by a small number of outliers in the feature space, but if those outliers cause large gradient signals, they can still skew the parameter estimates. Regularization is often employed to reduce sensitivity to outliers in parametric settings.

Non-parametric methods handle outliers somewhat differently. In k-Nearest Neighbors, an outlier is essentially a data point that’s far from the bulk of the distribution. It may not significantly impact the decision boundary for the majority of other points, but if your model query happens to be close to that outlier, the classification or regression decision can be skewed. Methods like decision trees (also typically considered non-parametric) can isolate outliers in small leaf nodes, which can lead to overfitting. On the other hand, ensemble methods like random forests average over many trees, partially mitigating the effect of outliers.

A subtle pitfall arises when you have “extreme” outliers that overshadow many other data points. With kNN, if the outlier is included in the dataset, it won’t affect predictions for most points—unless those points happen to be in the local neighborhood. But if your dataset has a high proportion of outliers, or if outliers exist in certain feature dimensions only, standard distance metrics can become misleading. In these scenarios, robust distance metrics or feature scaling strategies can be essential.

In terms of interpretability, how do parametric and non-parametric models differ, and what are some techniques to interpret non-parametric models?

Parametric models often come with a clear mathematical formulation. For linear or logistic regression, the parameters

correspond directly to the weight or influence of feature

j

on the prediction. This transparency makes parametric models relatively easy to interpret, especially if the number of features is not too large. Decision boundaries or regression coefficients can be explained to stakeholders in simpler terms, particularly if the model is linear or logistic.

Non-parametric models, especially those based on instance comparisons (e.g., kNN) or complex structures (e.g., random forests, gradient-boosted trees), can be less interpretable because they do not summarize their knowledge in a fixed parameter set. Instead, you can interpret non-parametric models using techniques such as:

• Feature importance measures: In random forests or other tree-based ensembles, you can measure how each feature contributes to decreasing impurity or error.

• Local surrogate models (e.g., LIME): You can train a simple, interpretable model (like a linear or decision tree model) around the neighborhood of a prediction to approximate how the bigger, non-parametric model behaves locally.

• Partial dependence plots or accumulated local effects (ALE): These show how changing one or two features while keeping others fixed influences model predictions.

A subtlety arises if your non-parametric model has a highly variable local structure. In that case, global interpretations become unreliable, and you may only be able to trust local interpretability methods around specific predictions. Additionally, in high-dimensional spaces, local interpretability itself can be challenging because neighborhoods can become sparse or less meaningful.

What special considerations arise when using parametric or non-parametric models for streaming data or online learning?

Streaming data or online learning refers to scenarios where data arrives continuously, and the model needs to update with new samples in real-time or near-real-time. Many classic parametric methods (e.g., linear models, logistic regression) have well-established online learning variants. You can incrementally update model parameters

θ

using methods like stochastic gradient descent (SGD). This update step is fast and memory-efficient, making parametric models often very practical for streaming or large-scale data. One subtlety is ensuring you pick a learning rate schedule that allows the model to converge while still adapting to changing conditions in the data stream.

Non-parametric models like kNN, in their raw form, can be more challenging to maintain in a streaming scenario. kNN typically stores all training examples, so for a never-ending stream, it’s infeasible to store all data indefinitely. You might need data summarization or sampling strategies. If you consider a tree-based model like a random forest in an online setting, you can incorporate incremental updates, but that typically requires specialized data structures or approximate methods. A naive approach that re-trains from scratch each time new data arrives is computationally expensive. Another subtlety is concept drift—when the data distribution changes over time. Parametric models can adapt by continually updating parameters, but they might forget older patterns that remain relevant. Non-parametric methods can adapt if they discard old data points or reweight them, but deciding how much to forget vs. retain can be tricky.

Are there cases where parametric models might actually require more data than non-parametric counterparts, despite the usual assumption that non-parametric models need more data?

While the common wisdom is that non-parametric models typically require more data to achieve good generalization, there are edge cases where parametric models might require extensive data to reliably estimate their parameters. For example, if you have a parametric model with a large number of parameters (like a deep neural network), the total number of parameters can be extremely high, even though it’s technically “parametric.” In such a high-parameter setting, you may need vast amounts of data to avoid overfitting.

Another nuance arises if your parametric model is misspecified—that is, if the true relationship does not conform well to the chosen functional form. You can end up needing a great deal of data to even approximate the correct relationship, and might still be outperformed by a carefully tuned non-parametric method that can capture nuances without strict functional assumptions. Additionally, certain small parametric models, if forced to represent a highly complex distribution, can become unstable or produce large variance in their parameter estimates without an abundance of data.

What are the differences in how regularization or constraints (like , penalties) are applied to parametric vs non-parametric models?

In parametric models, regularization is typically done by penalizing the magnitude of parameters

θ

. Common approaches include regularization (ridge), where you add a penalty term

, or regularization (lasso), where the penalty term is

. These reduce overfitting by shrinking parameter values, forcing the model to generalize better. Constraints like monotonicity or fairness constraints can also be integrated directly into the model’s objective or parameter domain.

Non-parametric models do not always have a fixed set of parameters to which you can easily apply these penalties. Instead, “regularization” can come in forms like:

• Limiting model complexity (e.g., restricting maximum depth in a decision tree or limiting the number of leaves).

• Adjusting hyperparameters (e.g., setting the number of neighbors k in kNN to a higher value to smooth predictions).

• Using smoothing parameters in kernel methods (e.g., bandwidth in kernel density estimation).

A subtle pitfall arises if you incorrectly assume that the same notion of regularization applies to both families. For instance, applying weight decay (an penalty) is straightforward in logistic regression, but in a kernel-based method or kNN, your primary “regularization” levers are quite different. Another complexity arises when implementing fairness constraints in tree ensembles or nearest-neighbor models: you might need specialized algorithms or data manipulation to ensure fairness objectives are met.

How does domain knowledge influence the choice between parametric and non-parametric methods, and can it be incorporated effectively in each approach?

Domain knowledge plays a pivotal role in model selection. If you have strong hypotheses about the data’s underlying structure—for instance, knowing that the relationship is likely linear or logistic in nature—parametric models can be more effective. You can hard-code domain constraints or transformations (such as polynomial expansions or custom features) that align well with your parametric structure. This can result in a simpler model that is easier to interpret and still quite powerful.

For non-parametric models, domain knowledge can guide your choice of distance metrics, kernels, or neighborhood sizes. For example, if your domain knowledge tells you that certain features are more relevant than others, you can weight those features more heavily in your distance calculation. Or if you suspect local stationarity in time-series data, you might use specialized kernel functions that reflect time-based similarity.

A subtle pitfall is incorrectly imposing domain knowledge that does not reflect the real distribution, leading to biases or over-constrained models. In parametric models, an incorrect assumption can cripple the model’s ability to fit the data. In non-parametric models, an incorrect kernel or distance metric might make it nearly impossible to find “true” neighbors. Balancing domain knowledge with empirical performance is an art; cross-validation and thorough experimentation help confirm if domain-driven choices are genuinely improving the model.

How do these approaches scale to multi-class classification or extremely large label spaces, and what nuances arise for parametric vs non-parametric methods?

In multi-class classification, parametric models like logistic regression typically employ strategies such as one-vs-rest or softmax regression (multinomial logistic regression). Softmax regression extends logistic regression to multiple classes by modeling the probability of each class as a normalized exponential function of linear scores. The parameter set becomes larger because each class typically has its own parameter vector, but training is still usually feasible using gradient-based methods.

For non-parametric methods like kNN, multi-class classification is straightforward in principle: you look at the class membership of the k neighbors. However, if your label space is extremely large (e.g., thousands or tens of thousands of classes), kNN can face serious computational challenges. You need to store enough representatives of each class to get reliable neighborhood estimates. Searching through a large dataset to find neighbors can become very expensive, requiring approximate nearest-neighbor algorithms and specialized data structures. Tree-based methods can handle multi-class classification by splitting on subsets of classes, but large label spaces can lead to deeper or more numerous trees if you attempt to separate many classes distinctly.

An edge case arises when the class distribution is highly imbalanced across a large label space. Parametric models might become dominated by the most frequent classes unless you reweight the loss function. Non-parametric methods might produce poor predictions for rarely observed classes because there are too few neighbors from those classes. Stratified sampling or specialized data augmentation may be required to ensure that minority classes are well-represented.

Are there unique hyperparameter tuning considerations for parametric vs non-parametric models beyond standard cross-validation?

For parametric models, hyperparameter tuning often involves selecting regularization strengths (e.g., the

λ

in ridge or lasso), choosing network architectures for neural networks, or deciding on polynomial degrees. Standard cross-validation works well, but you must be mindful of interactions between different hyperparameters (e.g., network depth, learning rate, regularization). Parametric models often have a relatively smaller number of hyperparameters compared to some sophisticated non-parametric approaches, but deep neural networks can have many architectural hyperparameters.

In non-parametric methods, hyperparameter tuning might involve the choice of neighborhood size in kNN, or kernel bandwidth in kernel density estimation, or tree depth in random forests. These hyperparameters can dramatically affect the model’s complexity. Cross-validation remains a cornerstone of tuning, but you may need specialized approaches like grid search or Bayesian optimization if your hyperparameter space is large. For example, in random forests, you might tune the number of trees, max features used in each split, minimum samples per leaf, etc. Each hyperparameter influences both bias and variance in sometimes non-intuitive ways.

A subtlety arises if your dataset is large and cross-validation becomes prohibitively expensive. You might resort to approximate or online hyperparameter selection methods. Another pitfall is overfitting to the validation set if you test too many hyperparameter configurations. Both parametric and non-parametric methods can fall into this trap, but non-parametric methods, being potentially more flexible, might require particularly careful scrutiny of your validation approach.

How do training and inference times compare for parametric vs non-parametric approaches, especially with specialized hardware accelerators?

Parametric models like linear/logistic regression generally have fast training times for moderate data sizes, and inference is extremely fast once parameters are learned, since prediction involves just a dot product or a small neural network forward pass. This speed advantage is especially pronounced on hardware accelerators like GPUs or TPUs, which are optimized for dense linear algebra operations. Neural networks, though large, also map well to GPUs or TPUs, resulting in potentially fast training and inference once properly parallelized.

Non-parametric methods often have relatively slow inference because you need to search or compare against a subset of the training data. kNN’s inference involves distance computations that scale with the training set size, which can be costly. Tree-based models like random forests also require traversing multiple trees per prediction. Though partial parallelization is possible, it typically doesn’t achieve the same speedups as parametric matrix operations on GPUs. Approximate nearest neighbor (ANN) techniques or specialized data structures (like KD-trees, Ball trees, or variants of vantage-point trees) can reduce the search complexity, but they introduce their own overhead and approximate factors.

A subtle pitfall occurs if your parametric model is so large (like a massive deep neural network) that you exceed memory capacity on your hardware accelerator. This can negate speed advantages or force distributed training. Non-parametric models might face similar scaling issues if the dataset is huge. Deciding how to partition or store the data across multiple machines can become a bottleneck. In resource-constrained environments, it’s often more practical to deploy a smaller parametric model with well-optimized code than a large non-parametric model that requires extensive memory access patterns during inference.

How does one handle or reduce model variance in non-parametric methods without sacrificing too much flexibility?

Non-parametric models are often highly flexible and can exhibit high variance, meaning small changes in the training data or query point can lead to different predictions. To manage this variance, you might employ:

• Bagging (Bootstrap Aggregation): For example, random forests average predictions over many bootstrapped decision trees, reducing variance substantially.

• Carefully chosen hyperparameters: For kNN, selecting a larger k smooths the decision boundary. For kernel methods, setting the kernel bandwidth carefully determines how “broad” or “narrow” the local region of influence is.

• Dimensionality reduction or feature selection: Reducing the dimensionality can help reduce variance by focusing on the most informative features.

The main pitfall is the bias-variance trade-off: while you reduce variance by restricting model complexity or averaging across multiple models, you might increase bias. For instance, in random forests, if you set max depth too low, you reduce variance but risk missing critical patterns. In kNN, setting k too large might overly smooth the decision boundary, losing subtle local structures. Striking the right balance requires thorough experimentation and validation. Another subtlety is that certain real-world data distributions can have local irregularities that are genuinely important. Over-smoothing might remove these crucial signals, so domain knowledge is often key to deciding how much to reduce variance.

What special pitfalls or edge cases can arise when combining parametric and non-parametric components in a single pipeline?

Hybrid approaches can be powerful. For instance, you might use a non-parametric step to extract local features (e.g., distances to nearest neighbors, or local density estimates) and then feed these into a parametric model as additional features. Or you might use a parametric model to embed data in a lower-dimensional space and then apply a non-parametric method in that embedded space. However, several subtle pitfalls can arise:

If the embeddings or features from the parametric model fail to preserve critical structure, the downstream non-parametric method might not perform well. Conversely, if the non-parametric step is poorly tuned, even a high-quality embedding from the parametric model may not yield good results.

There is also the question of interpretability. By stacking approaches, you may lose clarity on how final decisions are derived. Debugging becomes more complicated because errors might stem from either the parametric stage, the non-parametric stage, or interactions between them. Additionally, computational complexity can escalate if each stage significantly increases data dimensionality (e.g., a parametric method that outputs multiple transformations or derived features).

Finally, you could risk overfitting if the pipeline is not regularized or validated properly, especially if you tune parameters in both the parametric and non-parametric components simultaneously. Cross-validation needs to treat the entire pipeline as a single unit, ensuring you don’t leak information or overfit to the validation set by repeatedly adjusting the pipeline’s many moving parts.

---

Could a parametric model effectively become “non-parametric” if we keep adding more parameters or layers (e.g., deep neural networks), and what are the practical implications?

Even though deep neural networks can have millions or even billions of parameters, they remain “parametric” in the strict sense because the number of parameters is finite and fixed by the architecture. This is in contrast to non-parametric methods such as k-NN or Gaussian Processes, where the model complexity can expand with the dataset size itself. However, the boundary between “parametric” and “non-parametric” blurs in practice when the number of parameters is extraordinarily large compared to the training samples, or when sophisticated architectures (like transformers in NLP) are used. These networks can approximate highly complex functions and often exhibit behaviors reminiscent of non-parametric models (e.g., memorization in large capacity networks).

A key practical implication is how these high-capacity neural networks can overfit or memorize data if not properly regularized or if the dataset is too small. For instance, large language models trained on massive corpora can capture an enormous variety of patterns. Yet they still have a fixed limit on their representational power because the architecture imposes a finite—though huge—parameter count. In truly non-parametric scenarios, the capacity would keep growing as you add more data. Nonetheless, large parametric models can approximate this behavior closely when data is abundant.

Another consideration is that, while large parametric models may appear to behave similarly to non-parametric approaches in capturing complex decision boundaries, they still need carefully chosen architectures, hyperparameters, and optimization strategies to generalize well. Non-parametric methods, by contrast, shift the emphasis to the data itself rather than an elaborate, pre-specified architecture. Practitioners often realize that scaling a neural network’s size brings diminishing returns at some point unless there is a corresponding increase in data.

From a resource standpoint, extremely large parametric models can become expensive to train (due to gradient-based optimization over billions of parameters) whereas certain non-parametric methods, though also potentially expensive for storage or inference, can sometimes have more straightforward training (like storing data in k-NN). Thus, the complexity trade-offs differ considerably even if the final function approximations can both be extremely powerful.

Could we constrain a non-parametric method so severely that it behaves similarly to a parametric model, and in what scenarios would that be useful?

One way to constrain a non-parametric method is to limit how much of the training data it references or how it constructs the model boundary. For instance, a nearest-neighbor classifier can be restricted by reducing the size of its neighborhood search or implementing a fixed capacity data structure that prunes older data. If we keep a strict limit on how many samples are retained—for example, a small “window” of recent data or a small random subset—then effectively we reduce the model’s capacity to something that doesn’t grow with the entire dataset. This approach can make a non-parametric model look more “parametric-like,” as it won’t indefinitely expand its knowledge base.

In online or streaming scenarios, this approach might be extremely useful. If data arrives continuously, storing everything for k-NN or kernel methods may become intractable. A fixed-size buffer, plus a rule for discarding older or less relevant data, can keep the model’s memory usage bounded. Such constraints also reduce computational overhead at prediction time. Another scenario is real-time inference on embedded systems with limited resources. Constraining a non-parametric model’s capacity ensures that it can run within memory or power constraints.

The trade-off is that by imposing these constraints, you might lose the main advantage of a non-parametric technique—namely, its ability to leverage all available data to refine the decision boundary. You risk discarding relevant samples, which can degrade accuracy unless your subset remains highly representative of the original data distribution. Still, in practical systems, it can be a necessary compromise to fit real-world deployment requirements.

How do parametric vs non-parametric models handle multi-label or multi-output classification problems in real-world applications?

Multi-label classification involves assigning multiple labels simultaneously to a single instance. Parametric models like logistic regression can be extended to a one-vs-rest or multi-label framework by training a separate classifier (with its own parameter vector) for each label. Neural networks can use multiple output nodes—each producing a probability for a particular label—and train them jointly with, for example, a sigmoid activation per label. This approach can capture correlations among labels if the architecture is designed to do so (e.g., shared hidden layers).

In non-parametric models like k-NN, multi-label classification can be handled by letting the k neighbors “vote” for each relevant label. For instance, if an instance’s k neighbors have sets of labels, you might combine all neighbor labels with some frequency threshold to decide which labels to predict. Alternatively, you could treat each label as a separate classification sub-problem and run k-NN for each label individually. The advantage is that you don’t commit to a strict parametric form; the data determines the label relationships. The downside is that in high-dimensional, multi-label settings, distances may become less meaningful, and you might need advanced techniques or dimensionality reduction.

A subtle real-world issue arises when there’s an imbalance in label frequencies. For example, some labels might be extremely rare, making it difficult for parametric or non-parametric models to learn robust patterns. Specialized sampling techniques or cost-sensitive strategies can help. In parametric models, you might implement class weighting or focal loss to focus more on rare labels. In non-parametric methods, you could weigh neighbors differently (e.g., weighting by inverse frequency of labels) to mitigate label imbalance.

Are there any distinct strategies for calibration (turning raw model outputs into well-calibrated probabilities) when comparing parametric and non-parametric models?

Non-parametric models like k-NN do not inherently yield a smooth probability function; you often approximate a probability by counting neighbors of each class among the k nearest points. That ratio can serve as a probability estimate, but it might be noisy, especially in high-dimensional or sparse data settings. As with parametric models, you can apply isotonic regression or other post-processing steps to map these raw frequency-based predictions to better-calibrated probabilities.

One tricky edge case is when k is small or the data is highly imbalanced, leading to extreme probability estimates (e.g., 0/5 or 5/5). This can cause calibration problems. Smoothing techniques—like adding a small pseudocount (e.g., Laplace smoothing)—can mitigate these edge cases. Another subtlety is that non-parametric models might produce different probability estimates at each point because the local neighborhood can vary drastically depending on distribution. Sometimes, you might want to standardize the neighborhood or build specialized non-parametric probability estimators (like kernel density estimation) and then calibrate them.

What unique challenges arise when applying parametric vs non-parametric approaches to computer vision tasks?

In computer vision, data often involves high-dimensional images (e.g., thousands or millions of pixels). Parametric deep convolutional neural networks (CNNs) have become the de facto standard because they leverage specialized layers (convolution, pooling) that are extremely effective at extracting hierarchical image features. These parametric models can handle high-dimensional inputs by learning localized weight sharing patterns, significantly reducing the total parameter count compared to a naive fully connected approach.

A classic non-parametric method in vision might be a k-NN classifier over image embeddings. Instead of directly using raw pixel distances, practitioners often use features extracted from a pre-trained neural network. Once embedded in this lower-dimensional space, k-NN can act as a quick classifier. This approach can work well for tasks like few-shot learning: you embed your images in a feature space and then classify new examples by nearest neighbors among a small set of labeled examples.

A subtle challenge for purely non-parametric methods in vision is the curse of dimensionality. Raw images can make distance metrics uninformative, forcing an embedding step. Another pitfall is that storing and searching among a huge image database in real-time can be slow unless you use specialized indexing or approximate nearest neighbor techniques. Meanwhile, parametric CNNs require large labeled datasets and substantial compute resources to train effectively. If you have a small labeled dataset, you might rely on transfer learning from a network pre-trained on a large corpus (e.g., ImageNet), which is still parametric but drastically reduces the training data requirement for new tasks.

How do domain adaptation or transfer learning approaches differ for parametric and non-parametric models?

In parametric deep learning, transfer learning often involves taking a model pre-trained on a large dataset (such as a large language model or a CNN trained on ImageNet) and then fine-tuning its parameters on a new domain. This is possible because the model’s parameters (weights) capture rich representations that can be adjusted with a smaller amount of new data. Domain adaptation can also involve freezing some layers (to preserve general features) and retraining only the last few layers to adapt to the new task.

Non-parametric methods can also perform transfer learning, but they do so typically by reusing or augmenting the dataset. For example, in a k-NN approach, you might incorporate data from a related domain if it’s beneficial. One subtlety is deciding how to weight or select neighbors from different domains so that the model doesn’t overfit to domain-specific noise or get confused by dissimilar data. Another approach is to transform the feature space via a domain adaptation technique (e.g., domain-invariant embeddings) and then apply k-NN in this adapted space.

A unique pitfall in non-parametric transfer learning is that if the source domain is vastly larger, it can dominate the neighbor searches in undesirable ways. You may need weighting schemes or filtering strategies to ensure that only relevant samples from the source domain are considered. Another edge case is “negative transfer,” where including data from a different domain actually hurts performance because it introduces misleading neighbors or confounds distribution assumptions. Balancing these aspects can be more challenging compared to the structured approach of parametric fine-tuning.

In reinforcement learning, how do parametric vs non-parametric function approximators differ in policy or value function estimation?

In reinforcement learning (RL), you often need a function approximator for the policy (which action to take) or the value function (expected return). Parametric approaches typically use neural networks (Deep Q-Networks, policy gradients) or linear function approximators. These models can compactly represent a policy with a fixed parameter vector, but can struggle in very large or continuous state spaces unless carefully designed. Overfitting or catastrophic forgetting can occur if you don’t handle exploration and replay correctly.

Non-parametric approaches in RL might store experiences and query them to make decisions. One example is a nearest-neighbor method for value function approximation, where you look up states “similar” to your current state, see what actions led to high returns, and then derive your policy. This can be feasible in lower-dimensional spaces or when you store a large but finite set of experience states.

A subtle real-world issue arises if your state-action space is enormous (as in many real-world RL problems): a naive nearest-neighbor search becomes impractical. Another subtlety is that RL often involves continuously changing data distributions—states you explore at one point might differ drastically from states you see later. Parametric methods can be updated incrementally with gradient steps, whereas non-parametric memory-based methods may need sophisticated strategies to avoid storing an overwhelming amount of historical data. This tension highlights that parametric approaches often scale better in high-dimensional or continuous control scenarios, whereas non-parametric RL might only work well in specialized or smaller environments.

Could you elaborate on how regularization differs between parametric and non-parametric approaches, especially in practical deployments?

In non-parametric models, regularization can look different. For k-NN, choosing a higher k effectively regularizes the model by smoothing decision boundaries. In kernel methods, controlling kernel bandwidth or the complexity penalty in SVM (via hyperparameters such as C and kernel width) acts as a form of regularization. Another subtlety is data-driven regularization—for example, restricting the size of the data used (or weighting it differently) in a nearest-neighbor search. Decision trees can be pruned, or random forests can limit tree depth.

In practical deployments, a parametric model’s regularization is typically performed at training time (e.g., adding a penalty to the optimization). By contrast, non-parametric regularization often involves structural or hyperparameter choices (like k for k-NN, maximum depth for trees, bandwidth in kernel density estimation). An edge case arises when the dataset grows over time: parametric models might need re-training with updated regularization strategies, whereas non-parametric models need to manage data growth or decide how to “prune” their knowledge base. This difference can be critical in production settings where data streams in continuously.

How do we handle interpretability demands from regulatory bodies or stakeholders for parametric vs non-parametric models?

Interpretability can be essential in domains like healthcare, finance, or autonomous systems, where decisions affect safety or legality. Parametric models like logistic regression are often favored in regulated environments because their coefficients are relatively transparent—one can see which features are influential and in which direction. Even neural networks, though more complex, can sometimes be probed with explainability techniques like LIME or SHAP to highlight feature contributions.

Non-parametric methods can pose distinct interpretability challenges. k-NN might appear simple to explain conceptually (“We look at neighbors”), but in practice, it can be difficult to provide a high-level reason why certain neighbors are close or what general rules define the boundary. Decision trees can be more interpretable if they remain small, but ensembles of large trees (random forests) can become opaque. As a result, you might need specialized interpretability tools that show how many trees vote for a certain classification or which features are critical in the splits.

A subtle pitfall arises if regulated industries require robust explanations for every single prediction. Parametric linear models give a straightforward explanation by exposing weight coefficients. Non-parametric methods could require complex “local exploration” of the feature space to approximate reasoning behind each decision. Another real-world issue is that certain regulations might stipulate a maximum complexity or demand “human-friendly” explanations that are easier to provide with simpler parametric forms. Balancing the performance advantages of flexible, non-parametric methods with these regulatory constraints is a critical practical concern.

In industrial applications, how do you decide on parametric vs non-parametric approaches when factoring in model maintenance and iteration cycles?

Parametric approaches usually follow a clearer “train once, deploy, retrain as needed” cycle. Once you finalize the architecture or the parametric form, you can optimize the parameters on a training set, measure performance, and deploy the model. Updating the model means retraining or fine-tuning those parameters when new data arrives or distribution shifts occur. Maintenance involves versioning the parameter sets and ensuring stable reproducibility. This can be straightforward in well-structured MLOps pipelines because the model is represented by a fixed, finite set of weights or coefficients.

Non-parametric approaches may seem simpler to “train” initially (e.g., storing data for k-NN) but can complicate maintenance. As the dataset grows or distribution changes, you might need to remove outdated samples or incorporate new samples. There might not be a single “model file” to version-control easily; instead, you have the entire dataset or specialized index structures. Iterating on the model might mean reconfiguring the indexing or the hyperparameters controlling how neighbors are found.

Another subtlety is that performance improvements in non-parametric models can come from better ways of searching or structuring data (e.g., approximate nearest-neighbor libraries), rather than from param updates. So the iteration cycle might revolve around data engineering, indexing improvements, or hyperparameter tuning. In large-scale industrial systems, this can require more specialized infrastructure and can introduce overhead in storage and real-time query. On the other hand, parametric retraining can be computationally heavy for large neural networks, especially if frequent updates are required. Thus, an enterprise might choose a parametric method if it plans on stable, less frequent batch retrains, whereas a non-parametric approach might be more appealing if it can quickly incorporate new data without a full “retrain,” provided efficient indexing is in place.