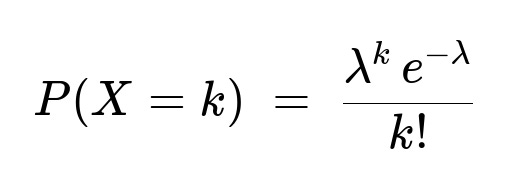ML Interview Q Series: Poisson Distribution: Calculating Probability of Few Chips in a Cookie
Browse all the Probability Interview Questions here.
A process for putting chocolate chips into cookies is random and the number of chips in a cookie follows a Poisson distribution with mean λ. Find an expression for the probability that a cookie contains less than 3 chips.
Short Compact solution
We sum the probabilities that the cookie has 0, 1, or 2 chips, because these are the possible outcomes less than 3. Using the Poisson formula and summing over k=0,1,2 yields:
Comprehensive Explanation
Poisson Distribution and Probability of Fewer Than 3 Chips
The number of chocolate chips X in a cookie is assumed to be Poisson-distributed with mean (or rate) λ. The Poisson distribution is used to model counts of events (in this case, chocolate chips appearing in a cookie) when these events occur randomly and independently, with a known average rate λ.
For a Poisson random variable X, taking non-negative integer values k = 0, 1, 2, ..., the probability mass function (pmf) is:
Here:
λ is the average (expected) number of chocolate chips per cookie.
k! is the factorial of k.
e is the base of the natural logarithm.
To find P(X < 3), we sum up P(X = 0), P(X = 1), and P(X = 2) because X < 3 corresponds to these integer outcomes:
P(X = 0) = e^(-λ) * (λ^0 / 0!) = e^(-λ)
P(X = 1) = e^(-λ) * (λ^1 / 1!) = e^(-λ) * λ
P(X = 2) = e^(-λ) * (λ^2 / 2!) = e^(-λ) * (λ^2 / 2)
Adding these yields P(X < 3) = e^(-λ) (1 + λ + λ^2 / 2).
Hence, the expression:
P(X < 3) = e^(-λ) (1 + λ + λ^2 / 2).
Interpretation
This result tells us the likelihood that a cookie will have no chips, exactly one chip, or exactly two chips. Because the Poisson distribution is discrete, we simply sum the individual probabilities. For a small λ, this probability will be relatively high, since the distribution is more concentrated at lower counts. Conversely, for a large λ, the probability of having fewer than three chips becomes very small, as the distribution shifts toward higher counts.
Example Calculation in Python
Below is a quick Python example to compute P(X < 3) for a specified λ:
import math
def poisson_prob_less_than_3(lmbda):
# Summation for k=0,1,2
total_prob = 0.0
for k in [0, 1, 2]:
term = (lmbda**k * math.exp(-lmbda)) / math.factorial(k)
total_prob += term
return total_prob
# Example usage:
lambda_value = 2.5
result = poisson_prob_less_than_3(lambda_value)
print(f"P(X < 3) for λ={lambda_value} is {result}")
In a practical Machine Learning or data science setting, one might rely on established libraries (e.g., scipy.stats.poisson) rather than coding the formula from scratch.
Potential Follow-Up Questions
How does Poisson differ from a Binomial distribution in this context?
In a Binomial distribution, we have a fixed number of independent trials n, each with a probability p of success. By contrast, the Poisson distribution effectively captures the probability of a given number of events in a fixed interval (or fixed “area”) when events occur with a known average rate λ, with no strict upper limit on the count. For large n and small p such that n*p = λ remains constant, the Binomial distribution approximates the Poisson distribution.
Why do we sum only the probabilities for k = 0, 1, and 2?
When we say X < 3, we specifically mean X can be 0, 1, or 2. Since X is discrete, the event X < 3 is the union of these three disjoint outcomes. Hence, probability theory tells us we can sum P(X = 0) + P(X = 1) + P(X = 2).
What if λ = 0?
If λ = 0, then we expect on average 0 chips per cookie. The Poisson probability becomes:
P(X = 0) = e^(-0) * (0^0 / 0!) = 1
P(X = k>0) = 0 Thus, P(X < 3) = 1 in that degenerate case, meaning we always have 0 chips.
How do we ensure numerical stability when λ is large?
For very large λ, terms like λ^k can be large and e^(-λ) can underflow. In practice, libraries like scipy handle such cases with logarithmic computations or specialized functions to maintain numerical stability. Python’s floating-point arithmetic can handle a fairly wide range of values, but specialized libraries are recommended when λ is extremely large.
How would this concept be used in a real-world ML or data-science project?
In an ML project, modeling counts of events (e.g., clicks, sensor readings, arrivals) is often relevant. You may use the Poisson distribution in a likelihood-based approach or a predictive model if counts of occurrences over an interval are of primary interest.
In anomaly detection, you might compare observed counts in a time period to the Poisson expected counts, and if the observed counts deviate significantly, it might be flagged as an anomaly.
Could we use a cumulative distribution function (CDF) for easier calculation?
Yes. The Poisson cumulative distribution function is P(X ≤ x). If the library provides a Poisson CDF, we can directly compute P(X < 3) = P(X ≤ 2). This approach often simplifies code and reduces manual summation errors.
By addressing these points in an interview, you demonstrate strong understanding of the Poisson distribution’s underlying mathematics, practical computation details, and common applications in data science and machine learning.