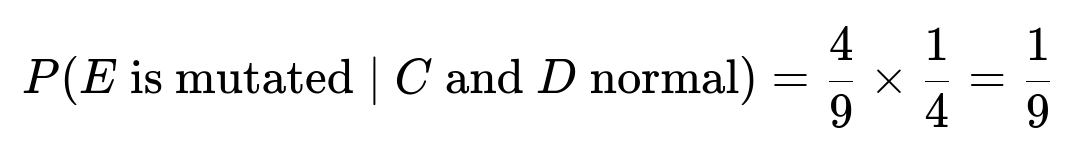ML Interview Q Series: Predicting Mutated Offspring Appearance Using Conditional Probability in Genetics
Browse all the Probability Interview Questions here.
An animal is considered normal when it either has two normal genes or one normal and one mutated gene, and it shows a mutated appearance only if it has two mutated genes. Each parent passes on one of its two genes at random with a 50% likelihood. Suppose there are two animals, A and B, each carrying one normal and one mutated gene. They produce offspring C and D, both of which appear normal. Then C and D mate and produce an offspring E. What is the probability that E has a mutated appearance?
Comprehensive Explanation
Every animal has two genes, each of which can be normal or mutated. If either one or both of these genes are normal, the animal’s external appearance is normal. Only when both genes are mutated does the animal appear mutated.
When an animal with one normal (N) and one mutated (M) gene reproduces, it can pass on either N or M with equal probability. Animals A and B each have the genotype (N, M). The offspring C and D are known to be phenotypically normal, which means they cannot both have mutated genes. C and D then produce E, and we want to find the probability that E ends up with two mutated genes.
Detailed Reasoning on C and D’s Genotypes
When two parents are each (N, M), the possible genotypes for any child are (N, N), (N, M), or (M, M). The chance for each child to have (M, M) in an unconditioned scenario is 1/4. However, C and D both appear normal, so (M, M) is ruled out for each of them.
Among the normal outcomes (N, N) and (N, M)/(M, N), the probability breakdown for a single child, given that it is normal, is:
(N, N) occurs with probability 1/3 (given the child is normal).
(N, M) occurs with probability 2/3 (given the child is normal).
Hence, given C and D are both normal, we have these joint probabilities for their genotypes:
C=(N,N) and D=(N,N) with probability 1/9.
C=(N,N) and D=(N,M) with probability 2/9.
C=(N,M) and D=(N,N) with probability 2/9.
C=(N,M) and D=(N,M) with probability 4/9.
Probability of E Being Mutated
If either parent is (N, N), it only passes N. Therefore, in all cases where at least one parent is (N, N), E cannot receive two mutated genes. The only scenario that produces (M, M) for E is when both parents are (N, M), which happens with probability 4/9 among normal C and D. In that case, each parent has a 1/2 chance of passing on the mutated gene, so E has a 1/4 chance of getting (M, M).
The combined probability that E appears mutated is therefore:
This means there is a 1/9 chance that E inherits two mutated genes and appears mutated, given that C and D are both normal.
Code Illustration in Python
import itertools
def possible_genotypes():
# A and B each have (N, M)
# Return list of tuples (genotype_of_child, prob) for a single child
# ignoring the child's final appearance here, just raw genotype distribution
# genotype_of_child could be ('N','N'), ('N','M'), ('M','N'), or ('M','M')
# Probability of each combination is 1/4
# We can handle (N, M) and (M, N) as same genotype for convenience if we want
return {
('N','N'): 0.25,
('N','M'): 0.25,
('M','N'): 0.25,
('M','M'): 0.25
}
# Calculate genotype distribution given the child appears normal
dist = possible_genotypes()
# Probability child is normal is sum of (N,N), (N,M), (M,N) = 0.25 + 0.25 + 0.25 = 0.75
# Probability of (N,N) among normal = 0.25 / 0.75 = 1/3
# Probability of (N,M) or (M,N) among normal = (0.25 + 0.25) / 0.75 = 2/3
# Check probability that both normal parents each have (N, M)
p_both_nm = (2/3) * (2/3)
# Probability that E ends up (M, M) if both parents are (N, M) = 1/4
p_E_mutated = p_both_nm * 0.25
print("Probability E is mutated given C and D are normal =", p_E_mutated)
Common Follow-Up Questions
Why are the genotypes of C and D considered independent given A and B?
They are independent because each offspring’s gene inheritance is a separate event, provided the parents’ genotypes are fully known and there is no additional condition that ties the genotypes of siblings together. The fact that C is normal does not change B’s or A’s genotype in a way that affects the probability distribution for D, because A and B are already fixed as (N, M).
How does conditioning on normal appearance affect the probabilities?
Conditioning on normal appearance means we exclude the (M, M) genotype from consideration. That exclusion redistributes the probabilities among the remaining genotypes. Originally, (N, N) would have probability 0.25, and (N, M)/(M, N) combined would have probability 0.5, which totals 0.75 for normal. When we condition on normal, these probabilities are scaled proportionally, yielding 1/3 for (N, N) and 2/3 for (N, M)/(M, N).
What if an alternative inheritance mechanism was at play?
In some genetic models, genes may not be passed to offspring with perfect 50–50 probability, or certain genes could be dominant/recessive in more complex ways than “normal vs. mutated.” In such cases, the probability computation and conditional reasoning would need to be adjusted according to the specific inheritance rules.
How do we handle real-world scenarios where multiple genes can affect appearance?
This interview-style question simplifies inheritance to a single gene pair. In reality, an animal’s phenotype often depends on many genes, and environmental factors can also influence whether a trait is expressed. The same fundamental conditional probability principles apply, but the combinatorial complexity grows, and more elaborate modeling approaches (like polygenic risk scores or Bayesian networks) may be needed.
Below are additional follow-up questions
If one of C or D was known to carry two normal genes, but the other’s genotype remained unknown, how would we refine the probability that E is mutated?
Having even partial information about a parent’s genotype can significantly affect our probability calculations. Suppose we learned that C is strictly (N, N). Then C can only pass normal genes to E. Hence, no matter what D’s genotype might be, E cannot inherit two mutated genes from a single (N, N) parent. In that scenario, E’s chances of being (M, M) would immediately be zero, since the best D could do is pass on one mutated gene. On the other hand, if we only know that D has a normal appearance without any additional testing, we must still consider that D could be (N, M). Even though (N, N) is possible for D, we would have to weigh both scenarios. But the guaranteed (N, N) status for C alone rules out the (M, M) possibility for E.
A potential pitfall is assuming that only one parent’s genotype matters. While it is true that if even one parent is strictly (N, N), E cannot be (M, M), real data might be incomplete or subject to testing errors (e.g., a lab test incorrectly labels C as (N, N)). This highlights the importance of data reliability when drawing conclusions in real-world genetic testing scenarios.
If we performed a genetic test on E and found exactly one mutated allele, how would that change our belief about C and D’s genotypes?
This question deals with Bayesian updating. Before testing E, we have certain probabilities for C and D’s genotypes based on their normal appearance. Once we discover E has one mutated allele, that tells us E definitely received that allele from at least one parent. This excludes situations where both parents might have been (N, N). Hence, after discovering E is (N, M), we would re-compute the distribution for C and D’s genotypes with the knowledge that E ended up with exactly one mutated gene. For instance, if both C and D were suspected (N, N) with some probability, that scenario is now impossible because E could not have received a mutated gene from (N, N).
A subtle issue arises if E is tested at an early developmental stage and results are uncertain—false positives or negatives would complicate the Bayesian update. Another pitfall is forgetting that some scenarios (like C=(N, N) and D=(N, N)) might still be partially assigned some probability if one miscalculates or fails to exclude them properly when new evidence emerges.
How would the probability of E being mutated change if we had five offspring from the same parents C and D, all appearing normal?
If C and D have multiple children, and all of them exhibit the normal phenotype, we might suspect that at least one parent is (N, N). That repeated evidence of no child ever being (M, M) can significantly reduce the likelihood that both parents are (N, M). Although each birth is an independent event in terms of gene selection, repeated observation of normal offspring is evidence that reduces the posterior probability of both parents having a mutated allele.
A potential pitfall is incorrectly assuming each child’s outcome is entirely independent of the others without updating our model of the parents’ genotypes. In real-world genetics, seeing multiple normal children in a row would push us to believe that both parents are less likely to carry mutated alleles. However, we must apply this reasoning carefully—there could be rare random outcomes (like repeatedly avoiding the mutated combination by chance) or incomplete penetrance in real genetic contexts.
Could external environmental factors or partial dominance affect the reliability of determining a mutated vs. normal phenotype?
Although the problem statement treats “normal” vs. “mutated” appearance as a clear binary trait dependent solely on the genotype (N, N), (N, M), or (M, M), real-world genetics often involves incomplete dominance, codominance, or external environmental influences. A gene might be mutated but not fully expressed, or an environment might suppress or trigger the trait.
This can lead to cases where an animal genetically (M, M) is phenotypically normal or an (N, M) individual might exhibit an intermediate phenotype. If such complexities exist, our probability-based approach to appearance may not be fully accurate. In interviews, mentioning this complexity shows awareness that Mendelian rules are often an oversimplification in the face of epigenetics or multifactorial inheritance. A major pitfall is forgetting that not all observed “normal” phenotypes map one-to-one with genetic normal alleles, especially in a large population where various factors might mask or enhance certain gene expressions.
What if the frequency of mutated genes is very low in the population, and A and B were chosen randomly from that population?
In the question, it is assumed that A and B each have one mutated and one normal gene. However, if the question evolved into a scenario where we only know the population distribution (i.e., a small fraction of animals carry mutated alleles), then the probability that both A and B are (N, M) might be extremely low a priori. A frequent pitfall is to assume we know the exact genotype of parents without questioning how that knowledge was obtained. In practice, one might need to incorporate population statistics and update the likelihood that A and B are carriers, given any test results or observed offspring phenotypes.
Another subtlety is that, in a scenario with very rare mutations, the chance that an individual with a normal phenotype is actually (N, M) might be very small. This reasoning is fundamental in genetic counseling, where prior probabilities (based on population genetics) must be weighed against new evidence from tests or offspring outcomes.