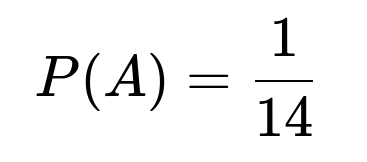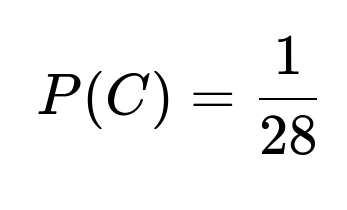ML Interview Q Series: Probabilistic Analysis of Semifinal and Final Encounters in a Knockout Tournament
Browse all the Probability Interview Questions here.
A tennis tournament is arranged for 8 players, randomly allocated over four groups of two players each. The winners of groups 1 and 2 meet each other in a semifinal match, and the winners of groups 3 and 4 meet each other in another semifinal match. In each match, either player has probability 0.5 of winning. Among these 8 players are John and Pete.(a) What is the probability that John and Pete meet each other in the semi-finals?(b) What is the probability that John and Pete meet each other in the final?
Short Compact solution
First define A as the event that John and Pete meet in the semi-finals. Let B1 be the event that they are allocated to the first two groups (groups 1 and 2) but end up in different groups. Let B2 be the event that they are allocated to the last two groups (groups 3 and 4) but again end up in different groups. One finds that P(B1) = P(B2) = 1/7. Using the law of total probability, one obtains P(A) = 1/14.
Similarly, let C be the event that John and Pete meet in the final. One can show that the probability of both being allocated in a way that places them on opposite sides of the draw is 2/7. Then again using conditional probabilities, the overall probability P(C) works out to 1/28. Another way to see this is to note that, by symmetry, every pair of players has an equally likely chance of meeting in the final, and there are 8 choose 2 = 28 possible pairs, so the probability is 1/28.
Comprehensive Explanation
The tournament setup is a standard knockout with 8 players divided into four distinct groups, each containing exactly 2 players. Each group’s winner advances to the semi-finals, where the winner of group 1 faces the winner of group 2, and the winner of group 3 faces the winner of group 4. The winners of these two semi-finals then play each other in the final. John and Pete are any two among these 8 players.
To understand the probabilities:
Step 1: Random allocation of 8 players into four pairs. Since the question is specifically about John and Pete, consider all ways to assign them to one of the four groups without concern for which other 6 players fill the other spots.
Step 2: Meeting in the semi-finals requires both John and Pete to win their respective groups and be placed in groups that face each other in the semis. There are only two pairs of groups that meet in the semis: (group 1, group 2) and (group 3, group 4).
Step 3: Meeting in the final requires John and Pete to be placed in opposite halves of the draw (one in groups 1 or 2, the other in groups 3 or 4), both win their groups, then each win their respective semi-final matches, thus facing each other in the final.
Probability of meeting in the semi-finals
To meet in a semi-final, they must:
End up on the same side of the draw, meaning both are placed in groups 1 or 2, or both in groups 3 or 4. However, they must not be in the same group because then they would meet in the first round, not in the semi-final.
Both need to win their respective first-round matches in order to meet in the semi-final.
A detailed enumeration or use of conditional probability arguments confirms that the result of this process yields 1/14. One outline of the reasoning is:
Probability that John and Pete are placed into groups 1 and 2 but not the same group is 1/7. The probability they then meet in the semi-final, given that placement, is the product of the probabilities they each win their group. Each has a 1/2 chance to win, so the combined chance is 1/2 * 1/2 = 1/4.
A similar calculation shows the probability is also 1/7 when they are placed into groups 3 and 4 but not the same group, with the same 1/4 chance of both winning and meeting in the semi-final.
Adding these (using total probability) gives 1/14 as the final probability.
Probability of meeting in the final
They can meet in the final only if they are placed in opposite halves of the draw (i.e., one in groups 1 or 2, and the other in groups 3 or 4), each wins their first match, and each wins the subsequent semi-final match.
By symmetry (or by explicit calculation), every pair of players among the 8 has exactly the same chance to face each other in the final. There are 28 possible pairs (since 8 choose 2 = 28). Thus the probability that John and Pete—one particular pair—face each other in the final is 1/28.
Alternatively, one can go through the same conditioning approach as with the semi-final calculation. Either perspective leads to the same final answer of 1/28.
Where P(A) is the probability of meeting in the semi-finals, and P(C) is the probability of meeting in the final.
Potential Follow-Up Questions
How exactly do you arrive at the 1/7 placement probability for B1 or B2?
If we concentrate on placing just John and Pete, we can assign John to one of the four groups first. The probability that Pete is placed in a different group but still in the same half (i.e., one of the two groups that meets John’s group in the semi-final) is computed by counting the possible slots available to Pete. Detailed combinatorial counting shows this probability is 1/7, but one can also think of it as:
John goes into, say, group 1. Pete must avoid group 1 but choose group 2 (to remain in the same half) among the remaining 7 positions. The probability that Pete chooses group 2 is 2 out of the 7 remaining slots. Then multiply by 1/2 because half of the time, John might be placed in groups 3 or 4, and you want Pete to go to the other group in that half. This careful breakdown yields the 1/7 figure.
The important insight is that only 2 of the 7 remaining slots place Pete correctly in the same half of the draw but a different group from John.
What if John and Pete end up in the same initial group?
Then they meet in the first round, which is not considered the semi-final or final. The probability that they meet in the first round is a separate event. In that scenario, only one of them progresses, so they cannot possibly meet again. For semi-finals or finals, they must start in different groups.
Could this probability change if the match-winning probabilities were not 0.5?
Yes, if one player had a different probability of winning each match, the calculations for P(A|B1) or P(A|B2) (and similarly for the final) would involve those modified probabilities instead of the simple 1/2 * 1/2. The structure of the problem would remain the same, but each conditional probability of them winning their group or winning the semi-final would be adjusted accordingly.
How can we verify the direct symmetry argument for meeting in the final?
If each player is equally likely to win any match, each of the 8 players is symmetric with respect to the others. Any pair of players is equally likely to end up clashing at any stage, subject to bracket constraints. In a single-elimination bracket of 8, exactly two players reach the final, so there are 8 choose 2 = 28 possible distinct pairs of finalists. Hence each pair has probability 1/28 of being the final matchup.
How do we generalize this result to 2^n players?
For a knockout format with 2^n participants, to find the probability that two particular players meet in the final, use a similar symmetry argument: there are 2^n choose 2 different pairs, and there is exactly one pair of finalists. Thus each pair has probability 1 divided by 2^n choose 2. A more complicated calculation might be required if the bracket is not a simple balanced bracket, but under a standard balanced design with all players equally likely to win, it generalizes in this way.
How would you simulate this in Python?
One could write a Python script that randomly assigns John and Pete to groups, simulates all matches with 50% win probability per match, and counts how often they meet in the semi-finals or finals, then compare those frequencies with the analytical results. A high-level simulation approach could look like this:
import random
def simulate_tournament(num_simulations=10_000_00):
meet_in_semis = 0
meet_in_final = 0
for _ in range(num_simulations):
# Randomly shuffle 8 players (including John and Pete)
# We'll label them: ["John", "Pete"] + 6 others
players = ["John", "Pete"] + [f"Player_{i}" for i in range(6)]
random.shuffle(players)
# Form groups: (players[0], players[1]) is group1, etc.
group1 = players[0:2]
group2 = players[2:4]
group3 = players[4:6]
group4 = players[6:8]
# Randomly determine winners with 0.5 probability
def winner_of(group):
return random.choice(group)
# Semi-final matches
semifinal_1 = [winner_of(group1), winner_of(group2)]
semifinal_2 = [winner_of(group3), winner_of(group4)]
# Winners of the two semis
finalist_1 = winner_of(semifinal_1)
finalist_2 = winner_of(semifinal_2)
# Check if John and Pete met in the semis
# They meet in semifinal_1 if it has both John and Pete
# or in semifinal_2 if it has both John and Pete
if ("John" in semifinal_1 and "Pete" in semifinal_1) or \
("John" in semifinal_2 and "Pete" in semifinal_2):
meet_in_semis += 1
# Check if they meet in the final
# That happens if finalist_1 == John and finalist_2 == Pete or vice versa
if (finalist_1 == "John" and finalist_2 == "Pete") or \
(finalist_1 == "Pete" and finalist_2 == "John"):
meet_in_final += 1
return meet_in_semis / num_simulations, meet_in_final / num_simulations
semis_prob, final_prob = simulate_tournament()
print("Estimated Probability of meeting in semis:", semis_prob)
print("Estimated Probability of meeting in final:", final_prob)
Over enough simulations, one would see the values converge close to 1/14 for the semi-finals and 1/28 for the final, confirming the analytical solution.
Below are additional follow-up questions
If the tournament bracket were seeded, would that change the probability calculations?
Seeding typically means that certain high-ranked players are placed into specific positions in the bracket. In this problem, the random allocation ensures that any player can end up in any group. If the bracket instead were seeded so that, for instance, the #1 seed is always placed in group 1, #2 seed always in group 2, etc., then the probability that John and Pete end up on a collision course might be very different.
One crucial difference is that seeds are typically designed to prevent strong players from meeting too early. For instance, in many tennis tournaments, #1 and #2 seeds are placed so that they can only meet in the final, not in earlier rounds. If John and Pete were seeds #1 and #2 respectively, then under standard seeding rules, they would be drawn in opposite halves. That directly implies a 0% chance of meeting in the semifinals (because they are in distinct halves that only converge in the final), and some positive probability of meeting in the final, typically higher than 1/28 (assuming they both progress).
A pitfall is that you can’t just say “it’s a seeded tournament” and apply the same 1/14 or 1/28 results. The entire bracket arrangement changes the distribution of how players are placed. Additionally, if the seeding rules place #1 in group 1, #2 in group 4, #3 in group 2, etc., the probabilities must be recomputed to reflect that structure.
How would the probability change if John and Pete have different chances of winning their matches?
In our original problem, the probability of winning for any player in any match is 0.5. If John has a probability p of winning a match and Pete has a probability q, then:
The probability they meet in the semifinals still depends on their placement in the bracket. But if they are placed in different groups within the same half, the conditional probability of both winning their first-round matches changes to p * q instead of 0.5 * 0.5.
Furthermore, if you also consider their meeting in the final, you must factor in that once they reach the semifinal, John’s chance of winning it might again be p (assuming we interpret p as his chance of beating any random opponent), and similarly for Pete. Realistically, p might vary depending on the opponent, but if we treat p and q as constants, we must carefully compute the chance that each man wins both his quarterfinal (group match) and semifinal.
A subtle pitfall is to assume p and q stay the same no matter the opponent, which may oversimplify real tournaments. Another subtlety is that these probabilities can also depend on whether John and Pete face each other (if they face each other, the probability of John winning might be p’, which could differ from p). Accounting for all of these intricacies can make the analysis more complex.
What if the tournament is double-elimination rather than single-elimination?
The original problem explicitly assumes a single-elimination knockout format. In a double-elimination format, each player must lose twice before being eliminated. This changes the bracket structure significantly and may allow the same two players (John and Pete) to meet more than once. Consequently, the probability that they face each other in a “semifinal” or a “final” is quite different, since there might be a “loser’s bracket final” and other matchups that feed into a grand final.
A key pitfall here is defining which match we call the “final.” In double-elimination, there is often a final match for the winner’s bracket and a potential “grand final” if the loser’s bracket winner defeats the winner’s bracket champion once. The question “meet in the final” might refer to that very last possible match or the winners’ bracket final, so precise definitions matter. The bracket shape and matches are far less straightforward, requiring new probability trees or combinatorial logic for each stage.
How does the probability of meeting change if the tournament uses a random draw every round instead of a fixed bracket?
Some events use a fixed bracket from the start, whereas others might re-draw players in each new round. For example, after the four group winners are determined, the tournament might randomly pair them for the semifinals instead of having 1 vs 2 and 3 vs 4. That changes the probability structure for who meets whom in each round.
If a new random draw is performed at each stage:
For the semifinals, all 4 winners are placed into a random bracket. The chance that John meets Pete there is the chance that they both have won their group (each having probability 0.5 in the first round if we still assume 50-50) and are then drawn together among the 4 remaining players. If John and Pete are among those 4, the chance that they are paired is 1/3 (because once John is chosen, Pete has a 1/3 chance of being selected as his opponent out of the three other semifinalists).
For the final, if they both reach the semifinals, the bracket is presumably set at that point, or if it’s re-drawn again after the semifinals, the logic changes further. The main pitfall is that you cannot apply the old bracket-based logic to a scenario with repeated random draws. Each round’s pairing mechanism has to be examined individually.
What if there are byes or uneven distribution of players in the first round?
Sometimes, tournaments with 8 players are fully bracketed, but imagine a scenario where a tournament might give a first-round bye to two players. A “bye” means a free pass to the next round. That can alter the structure significantly:
John or Pete could have a bye and thus skip the first round entirely.
This changes the total number of matches and how the bracket converges.
If John or Pete has a bye, then the probability of them eventually encountering each other is typically increased, because skipping a round raises the chance of reaching later rounds.
A common pitfall is to assume that the probability remains the same even with byes. In reality, who gets the byes, how many byes exist, and how the rest of the bracket is arranged can heavily influence the likelihood of certain matchups.
Is there a possibility that John and Pete might play a best-of-three or best-of-five match, and would that affect the probability of meeting?
In a simple sense, whether a match is best-of-three or best-of-five does not change who ultimately advances—only the distribution of possible ways a match can be won or lost. If each player still has an overall 0.5 chance to win the match, the structure is unaffected by the format of the match. The probability of them meeting is determined primarily by bracket placement and who advances, not by how many sets are played.
A subtle consideration arises if the best-of-five format changes each player’s probability of winning overall (for example, if the better player is more likely to prevail in a best-of-five). If John or Pete is consistently the stronger player, best-of-five might give him a higher probability of winning, hence changing the chance that he moves on and can meet the other at a later stage. The main pitfall is ignoring that best-of-five can shift the odds if you assume skill levels differ from 50-50.
How does the probability change if we know that one of them (say, Pete) definitely wins the first-round match?
Sometimes additional information is revealed partway through a tournament. If we learn that Pete is guaranteed to advance from his first match, we need to condition on that event. For example:
Probability(They meet in the semifinal | Pete already in the semifinal) is now the probability that John also wins his group (assuming a 0.5 chance) times the probability that their groups are in the same half but not the same group. One has to re-normalize over possible placements of John that make sense given what we know about Pete.
For the final, you similarly factor in the updated knowledge that Pete is already past his first match, and recalculate the bracket scenarios in which John can still meet Pete.
A subtle pitfall is forgetting to properly condition on new information and inadvertently counting placements or outcomes that are no longer possible.
Could the probability of meeting be influenced by external constraints, like scheduling or TV coverage?
Some real-life tournaments may adjust their brackets mid-way through for viewership reasons or scheduling conflicts, though this is quite unusual in formal tennis events. If, hypothetically, the organizers manipulate draws so that high-profile players do not meet until later rounds, that changes the probability distribution.
A pitfall is to assume tournaments are always fair and strictly bracketed. In smaller or local tournaments, organizers might rearrange to accommodate logistical concerns, so the theoretical results no longer hold. You would have to specify how the rearrangement is done (purely random, or ensuring certain players are kept apart) to recast the probability model accurately.
What if we wanted the probability that they meet at least once at any stage?
So far, we focused on the probability of meeting in a specific round: semifinals or final. But one might wonder: what’s the probability they face each other at any point during the entire knockout? That includes:
The probability they meet in the first round if allocated to the same group.
OR they meet in the semifinal if allocated to the same half but different groups and both win their first matches.
OR they meet in the final if they are in opposite halves and both progress.
You would add these probabilities, but be careful not to double-count scenarios. For instance, if they meet in the first round, that precludes meeting in a later round. This is a bigger sum of events that are mutually exclusive (meeting in Round 1, or meeting in the Semis, or meeting in the Final). A common pitfall is ignoring that “meeting in the semis” depends on them not having met in Round 1, and so on.
How do we handle a scenario where more players are added mid-tournament as wild cards?
In some informal settings, you might see tournaments where new players join in later rounds, or special “wild card” entries are slotted into the second round. This is highly unorthodox for typical tennis tournaments, but it can occur in certain open events or other sports contexts. In that case, the bracket is no longer a closed 8-player system. The presence of new players changes the structure of who meets whom.
A subtle pitfall is to treat new entries as if they had been in the original bracket. Instead, one must treat the bracket as partially known up front and recalculate the possible matchups once the new players appear. Typically, no standard tennis event does this, so it’s more of a hypothetical scenario illustrating how real-world constraints or unusual formats can complicate the neat 1/14 or 1/28 logic.
How might these results extend if we look at an n-round knockout with 2^n players but we only focus on whether John and Pete meet in round k?
One could generalize: with 2^n players, each round halves the field. Rounds are enumerated from 1 (the first round) up to n (the final). If we want the probability of John and Pete meeting specifically in round k (1 <= k <= n), the bracket structure determines which subset of players can face each other in that round. You would count the ways to place John and Pete so that they land in the same “segment” of the bracket of size 2^(n-k+1) but in different “segments” of smaller groupings if needed. Then multiply by the probability both advance from the earlier rounds.
Common pitfalls include incorrectly summing probabilities across rounds (they can’t meet in two different rounds in the same tournament, so events are mutually exclusive), or forgetting to account for the need for each to win all matches leading up to round k. Analyzing it in general form requires careful combinatorial partitions or leveraging symmetry arguments about equally likely draws.