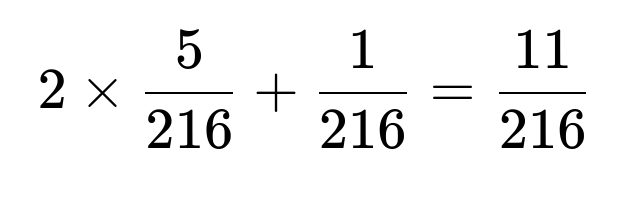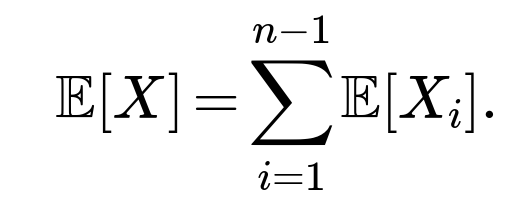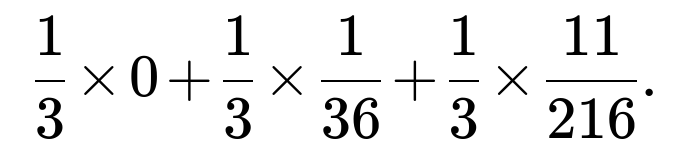ML Interview Q Series: Probability: Calculating Consecutive Sixes in Three Die Rolls
Browse all the Probability Interview Questions here.
You roll a fair six-sided die three times. What is the probability that you observe a pair of sixes on consecutive rolls?
Short Compact solution
Observe that there are only two distinct ways to get consecutive sixes: either they appear on the first and second roll, or on the second and third roll. In the scenario where exactly two consecutive sixes appear (and the third roll is not a six), the probability is twice the product of the chance of not rolling a six on one roll and rolling two sixes on the other two. This is:
Additionally, there is the chance that all three rolls are sixes, which has probability
Summing these probabilities gives
Comprehensive Explanation
One way to see why the probability is 11/216 is to systematically list all possible outcomes of rolling a fair six-sided die three times. There are 6×6×6 = 216 possible ordered outcomes in total. Among these, we count the outcomes where at least two consecutive rolls are sixes:
First possibility is (6, 6, not 6). There are 5 choices for that “not 6” outcome, so 5 possible sequences. Second possibility is (not 6, 6, 6). Again, there are 5 choices for “not 6” in the first position, giving 5 sequences. Third possibility is (6, 6, 6). That is just 1 sequence.
When these are combined, there are 5 + 5 + 1 = 11 favorable outcomes out of 216 total. Hence, the probability is 11/216.
Another way is to consider separate probabilities for exactly two sixes in a row (while the non-consecutive roll is not six) plus the probability that all three rolls are sixes. In the exactly-two-consecutive-sixes scenario, we have either consecutive sixes on rolls 1 and 2 with roll 3 not a six, or consecutive sixes on rolls 2 and 3 with roll 1 not a six. That probability turns out to be (5/108) in total. The chance that all three are sixes is 1/216, leading to a final probability of (5/108) + (1/216) = 11/216.
It is critical to treat the “all three are sixes” case separately rather than attempting to multiply or add the consecutive-sixes cases without proper adjustment. Overcounting can occur if you fail to recognize that the scenario with three sixes is included in both of the “first-two-consecutive” and “second-two-consecutive” calculations.
Reasons this approach works include: It enumerates all possible ways to get two sixes in a row by explicitly distinguishing between exactly two consecutive sixes and all three sixes. It accounts for the probability that the single non-consecutive roll (if it occurs) is not a six. It ensures no double-counting of the all-three-sixes scenario.
Applying the general principle of counting or using probability rules carefully avoids logical missteps, especially regarding overlap cases and complements.
Implementation Example in Python
import itertools
faces = [1, 2, 3, 4, 5, 6]
count_consecutive_sixes = 0
total_outcomes = 6**3
for outcome in itertools.product(faces, repeat=3):
# Check if there are consecutive sixes
if (outcome[0] == 6 and outcome[1] == 6) or (outcome[1] == 6 and outcome[2] == 6):
count_consecutive_sixes += 1
probability = count_consecutive_sixes / total_outcomes
print(probability)
The output should be 11/216 if you run this code.
Pitfalls and Edge Cases
One subtlety involves accidentally counting the scenario with three sixes multiple times. It appears in both “first and second roll” and “second and third roll” consecutive-six calculations. You must either subtract or avoid double-counting by clearly separating “exactly two consecutive sixes” from “all three are sixes.”
Another pitfall is mixing up the logic between having “at least two consecutive sixes” and “exactly two sixes total.” Those are very different probabilities and require different counting techniques.
Why 11/216 is the final answer can also be rationalized by focusing on complement probabilities (though that can be more cumbersome in this particular question) or by listing out sequences systematically.
How would this change if we needed two sixes in a row among ten rolls?
Answer
When the sequence of rolls is extended to ten, the probability of seeing at least two sixes in a row is much larger. One strategy is to use the complement event: “No two consecutive sixes appear at all.” We could then calculate the probability of that event and subtract from 1.
The complement approach works by noticing that if no two consecutive sixes appear, then after every six there must be a non-six. This can be represented by a recurrence or Markov chain approach. In a dynamic programming style, you can track states like “How many ways (or with what probability) can we be in a state where the last roll was a six, or the last roll was not a six?” and so on.
To do this manually would be a bit more involved than in the three-roll scenario. Typically, you would define:
A(n) as the number of valid sequences of length n that do not contain consecutive sixes and whose last roll is not six. B(n) as the number of valid sequences of length n that do not contain consecutive sixes and whose last roll is six.
Use initial conditions for n = 1 or n = 2 and iterate up to n = 10. The ratio of A(10) + B(10) to the total 6^10 would give the probability of having no consecutive sixes. Then 1 minus that would yield the probability of at least one instance of two sixes in a row. A Markov chain approach or matrix exponentiation can also handle this systematically.
What if we wanted the exact number of times we get two sixes in a row?
Answer
If the question is about exactly how many distinct pairs of consecutive sixes appear in the sequence, you would need to count all possible sequences where we have precisely one occurrence of consecutive sixes, or exactly two occurrences, and so on. For instance, in a ten-roll sequence, it is possible to have multiple disjoint pairs of consecutive sixes or even overlapping ones if you count something like (6,6,6) as two overlapping occurrences. Careful combinatorial arguments or dynamic programming are commonly used to enumerate or compute these probabilities. The dynamic programming strategy would involve states that remember whether the last roll was a six and whether you just formed a consecutive pair, proceeding step by step.
How would the probability change if the die was biased?
Answer
With a biased die, say the probability of rolling a six is p and the probability of rolling any other face is (1 – p) distributed among the remaining five faces, the logic remains the same but with probabilities replaced accordingly. For three rolls, the chance of exactly two consecutive sixes (and not a six on the third roll if the pair is in the first two rolls) would be 2 × p²(1 – p) if we only want exactly one pair of consecutive sixes, plus p³ for the case of all three sixes. Summation yields 2 × p²(1 – p) + p³ = 2p² – 2p³ + p³ = 2p² – p³. This reasoning generalizes to more extended sequences via either direct enumerations or Markov chain-based methods.
Is there a Markov chain interpretation for the three-roll scenario?
Answer
Yes. A Markov chain approach categorizes states based on how many consecutive sixes have occurred so far. For a three-roll experiment, you can track states such as “no six in the previous roll,” “exactly one six in the previous roll,” “two consecutive sixes,” etc. Then you transition between states based on whether you roll a six or not. It can feel like overkill for just three rolls, but it showcases a systematic method to analyze longer sequences. If you had many rolls, you would build a small state transition matrix that captures how you move between “no recent six,” “one recent six,” and “two consecutive sixes,” and keep track of probabilities step by step. For three rolls, manual counting is simpler, but the Markov chain approach makes the method straightforward to extend.
Could this be generalized to consecutive outcomes of different faces?
Answer
Certainly. If the requirement was “consecutive identical faces,” not just sixes, you would scale the counting appropriately. With an unweighted die, each face has a 1/6 chance, so consecutive sevens or consecutive fours or any other face follows the same pattern of analysis, except you would now need to look at any face repeated consecutively. The probability would be higher than specifically looking for sixes, because multiple faces can fulfill the requirement. The counting techniques or the Markov chain formalism remain largely the same, just adapted to more possible triggering outcomes.
These questions demonstrate common expansions and variations of the “consecutive faces” problem, which is often used to gauge understanding of probability fundamentals, combinatorial enumeration, and advanced methods like Markov chains or dynamic programming.
Below are additional follow-up questions
If the question asked for “exactly two consecutive sixes” (excluding the case where all three are sixes), how would the probability differ?
A natural extension is to separate the probability of at least two consecutive sixes into two disjoint events:
Exactly two consecutive sixes and the third roll is not six.
All three rolls are six.
When a question asks for the probability of exactly two consecutive sixes, it excludes the scenario with three sixes in a row. Therefore, you only consider the cases:
First and second rolls are sixes, but the third roll is not six.
Second and third rolls are sixes, but the first roll is not six.
Each of those events has probability:
There are two such placements (either rolls 1–2 or rolls 2–3), giving a combined probability of
Hence, when you exclude the event of rolling three sixes, the probability for exactly two consecutive sixes is (10/216). This value is less than (11/216) because you are removing the overlapping scenario (three consecutive sixes).
Potential Pitfall: Some candidates might forget to exclude the case of rolling three sixes, inadvertently double-counting or mixing up “at least two consecutive sixes” with “exactly two consecutive sixes.” Always carefully check if the question includes or excludes the possibility of three sixes in a row.
How do we calculate the expected number of times two consecutive sixes appear if we extend the experiment to more rolls?
To determine the expected count of occurrences of “two consecutive sixes” over multiple rolls (for instance, n rolls), you need to consider each pair of adjacent rolls. For n rolls, there are ((n-1)) pairs of consecutive rolls. Define an indicator random variable (X_i) that is 1 if the (i)th pair (rolls (i) and (i+1)) are both six, and 0 otherwise. The total number of times two consecutive sixes appear is:
The expectation of (X) follows from linearity of expectation:
Since each roll is a fair, independent event, the probability that a given pair is two sixes is ( \frac{1}{6} \times \frac{1}{6} = \frac{1}{36} ). Therefore, (\mathbb{E}[X_i] = \frac{1}{36}). Summing across all ((n-1)) pairs:
Potential Pitfall: One subtlety is that these pairs can overlap. For example, in the sequence (6,6,6), there are two overlapping occurrences of consecutive sixes. Nevertheless, linearity of expectation holds even if random variables are correlated. This is a frequent stumbling block: many worry that overlaps “break” the formula, but linearity of expectation does not require independence. So you can straightforwardly compute the expected count without extra corrections.
If we already know the result of the first roll, how does that information update the probability of observing two consecutive sixes in three total rolls?
When partial information is revealed, conditional probabilities come into play. Suppose you observe the first roll and want the revised probability that by the end of three rolls you have at least one instance of two consecutive sixes. Consider two cases:
Case 1: The first roll is a six.
Then to get two consecutive sixes in three rolls, you only need the second roll to also be six. If that happens, you have your two consecutive sixes immediately (rolls 1 and 2). Even if you miss on roll 2, you could still get consecutive sixes on rolls 2 and 3 if roll 2 or 3 ended up being six in some pattern. But the most direct route is that if roll 2 is six, you are already done. This changes the probability from the unconditional 11/216 to something higher because the first roll is already six.
Formally, let (A) = “two consecutive sixes in the three-roll sequence,” and let (B) = “the first roll is six.” We want (P(A | B)). We can break down the next two rolls and count how many ways two consecutive sixes can occur given that we started with a six.
Case 2: The first roll is not a six.
Now the only chance to get two consecutive sixes is if rolls 2 and 3 are both six. The probability of that event happening is ( \frac{1}{6} \times \frac{1}{6} = \frac{1}{36} ). This is a simpler scenario because you lose the possibility of getting a pair on rolls 1 and 2.
Hence, your updated probability depends on the observed outcome of the first roll:
If the first roll is six, the conditional probability is higher than (\frac{11}{216}). Detailed enumeration or direct conditional probability formulas can be used:
If roll 2 is six, you instantly have consecutive sixes, and that occurs with probability (\frac{1}{6}). If roll 2 is not six, you can still get a pair if roll 2 = not six and roll 3 = six, but that only yields consecutive sixes if roll 2 also ended up being six, which it isn’t. So you’d specifically be looking for (6,6,x) or (6,x,6) with x not necessarily non-six, because if roll 2 is not six, that breaks the consecutive chain, so you only have the possibility that roll 2 is six and roll 3 is six if that second scenario is being counted. An explicit enumeration is best here.
If the first roll is not six, you only get the pair on rolls 2 and 3, so the probability is (\frac{1}{36}).
Potential Pitfall: A common mistake is ignoring the knowledge of the first roll or incorrectly mixing up the separate conditional cases. Always split by the event “first roll is six or not six” and analyze each branch properly.
What if the dice are physically large or small, or the rolling mechanism is unusual? Does that affect the assumption of independence?
From a purely mathematical perspective, rolling any fair six-sided die yields independent trials: each outcome does not affect the next. However, in real-world situations with physically unusual dice (for instance, extremely large foam dice that might systematically land on certain faces more often, or dice rolled in a contraption where the outcome might be biased), the independence assumption can break. The probabilities might shift or become correlated from one roll to the next.
Examples of how real-world biases might arise:
If the surface is not level, certain faces may be favored.
If a person’s rolling style is consistent in a particular pattern (e.g., always landing with a high face up).
If the dice have minute differences in weight distribution (loaded dice).
To handle real-world issues, one might conduct many experimental rolls, gather empirical data on the frequency of each face, and then assess whether consecutive outcomes are correlated. A standard independence-based theoretical model would be adjusted using these observed frequencies and correlation estimates.
Potential Pitfall: Candidates might forget that “independence” is an assumption. It can be incorrect in physically constrained conditions, so always confirm if real-world data matches or diverges from the theoretical ideal.
Could two sixes in a row be treated as a “success” in a repeated Bernoulli process if we roll sets of three dice many times?
Imagine you repeatedly roll a die three times, observe whether you got consecutive sixes, and then reset. Each set of three rolls is an independent “trial” that results in a success (yes, consecutive sixes) or a failure (no, consecutive sixes). The probability of success in any given set of three rolls is (\frac{11}{216}). This is effectively a Bernoulli process with parameter (p = \frac{11}{216}).
Once you define each triple-roll set as a single trial, you can ask questions like: “How many successes out of N sets do we expect?” or “What is the variance in the count of successes?” The expectation would be (N \cdot \frac{11}{216}). The random variable counting the number of successful sets follows a Binomial((N, \frac{11}{216})) distribution.
Edge Cases and Pitfalls:
Overlapping sets of three rolls are not truly independent if you slide the window (e.g., consider rolls 1,2,3 as one set and 2,3,4 as another set). This leads to correlation. For the Bernoulli viewpoint to hold exactly, each triple is entirely separate and does not share rolls with another triple.
If the same dice are used in varying conditions (like temperature or mechanical differences), the assumption that each triple has the same success probability might fail over time.
If we change the question to, “at least two consecutive sixes in any number of rolls from one to three,” is that a different probability?
Yes. If the number of dice rolls could be 1, or 2, or 3, chosen at random (say each with probability 1/3), then the overall probability of seeing two consecutive sixes becomes a weighted combination:
With only 1 roll, it is impossible to have two consecutive sixes, so probability = 0 in that scenario.
With 2 rolls, the probability of consecutive sixes is (\frac{1}{36}).
With 3 rolls, the probability is (\frac{11}{216}).
Hence, if you randomly decide whether to roll 1, 2, or 3 times, each with probability 1/3, your final overall probability of “two consecutive sixes” is:
Potential Pitfall: Mixing up or ignoring which random scenario you are in can lead to an incorrect aggregated probability. This is a classic “law of total probability” application. One must carefully weight each conditional probability by the probability of that condition (in this case, the number of rolls).
Is there a scenario where rolling two dice at once each time changes the probability of consecutive sixes?
If the question is reinterpreted so that “consecutive sixes” means “two dice from successive throws both show six,” we must ensure the structure is consistent. Rolling two dice simultaneously at each “step” can create confusion about what “consecutive” means. Usually, consecutive rolls refer to outcomes from the same single die over multiple throws. If you throw two dice simultaneously, you might ask: “Do both dice in one throw show six, or do I look at dice from separate throws?”
If you interpret “consecutive throws” as each pair of time steps, then for a single die that is thrown once per time step, the situation is the same as the standard “one die over multiple throws.”
If each time step has two dice thrown, you must define whether you are checking if die1 on throw t and die1 on throw t+1 are both six, or if you might mix die1 on throw t and die2 on throw t+1, etc. Usually, you keep track of each die separately if you want a “consecutive” concept for that die’s outcomes.
Potential Pitfall: Confusing “two dice at once” with “two consecutive sixes in a single die’s sequence” or mixing up which die is which can lead to complicated or inconsistent definitions of consecutive. Always clarify how “consecutive” is being tracked: does it apply to the same physical die, or across dice, or across time steps?
What if we allow the event “two consecutive sixes” to count overlapping occurrences more than once? Would that change anything in a three-roll scenario?
In three rolls, the only way an overlap can occur is if you get three sixes in a row, which contains two overlapping pairs of consecutive sixes: (Roll1, Roll2) and (Roll2, Roll3). If the question were, “How many total pairs of consecutive sixes occur in three rolls?” the distribution can be:
0 if no pairs of consecutive sixes appear.
1 if exactly two consecutive sixes appear (but not a third).
2 if all three rolls are sixes (overlapping pairs).
Hence, counting occurrences or weighting each pair separately is relevant if you care about “how many pairs total” rather than just “at least one pair.” In that scenario:
Probability of 2 occurrences in three rolls = Probability(all three are six) = (1/216).
Probability of 1 occurrence in three rolls = Probability(exactly two consecutive sixes) = (10/216).
Probability of 0 occurrences = (205/216).
Then you could define an expected value for the total number of pairs found in three rolls:
E[# of consecutive-six pairs] = 0 × (205/216) + 1 × (10/216) + 2 × (1/216) = 10/216 + 2/216 = 12/216 = 1/18.
Potential Pitfall: Overlapping events like (6,6,6) produce two distinct pairs of consecutive sixes, which some might mistakenly count as just one or incorrectly ignore. Always clarify whether you are counting pairs as separate events (even if they overlap) or simply checking if at least one pair occurs.