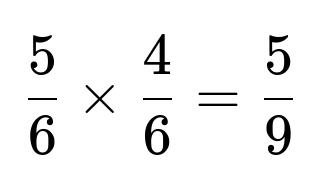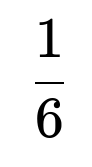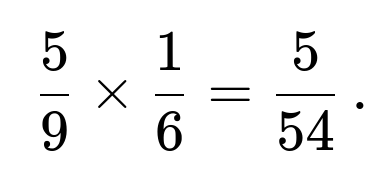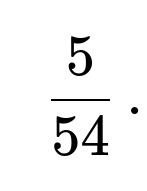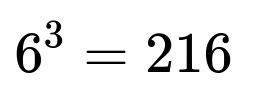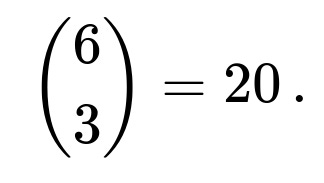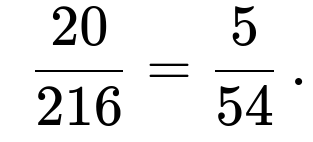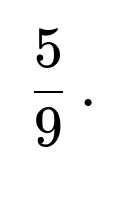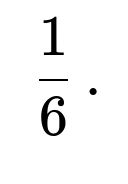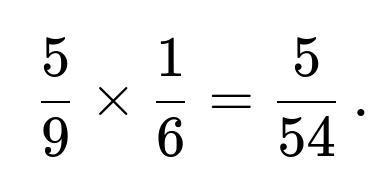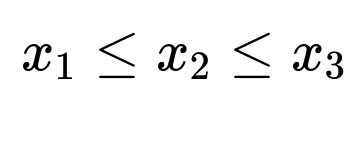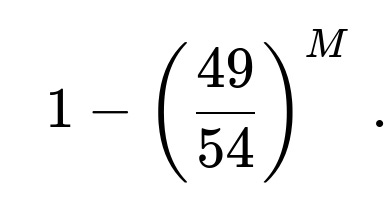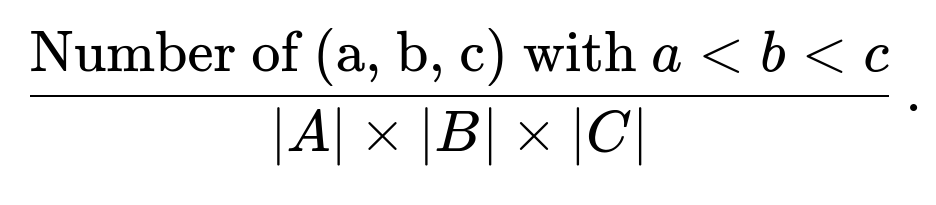ML Interview Q Series: Probability of a Strictly Increasing Sequence from Three Dice Rolls

Browse all the Probability Interview Questions here.

You roll a fair, six-sided die three times in a row. What is the probability that the three outcomes form a strictly increasing sequence?

Short Compact solution

First, all three results must be distinct; if any two are the same, a strictly increasing pattern is not possible. The probability that the three rolls show three different values is

because, after the first roll, the second has a 5/6 chance of differing from the first, and then the third has a 4/6 chance of differing from the previous two.

Given that the three numbers are distinct, there is exactly one way (out of the 3! possible permutations of three distinct numbers) that arranges them in strictly increasing order. Therefore, the conditional probability of getting a strictly increasing pattern, once we know they are all different, is

Multiplying these two probabilities gives

Hence, the probability of obtaining three strictly increasing outcomes from three successive dice rolls is

Detailed Explanation and Reasoning

Overview of the total possible outcomes

Whenever you roll a fair six-sided die three times, the total number of outcomes is

because each roll can result in one of six possible values independently. We are interested in the proportion of these 216 outcomes that satisfies “strictly increasing” results, meaning the value on the second roll must be greater than the first, and the value on the third roll must be greater than the second.

Two primary methods to calculate this probability

Method 1: Counting all strictly increasing triplets directly

• Each strictly increasing sequence of length 3 must pick three distinct numbers out of the set {1, 2, 3, 4, 5, 6}.

• The count of ways to choose three distinct numbers out of six is

• For each choice of 3 distinct numbers, there is exactly one way to place them in strictly ascending order.

• Thus, there are 20 favorable outcomes. The total outcomes are 216. This directly gives a probability of

  

  Method 2: Using conditional probabilities

  • As explained in the short solution, the probability all three values are distinct is

    

    Given three distinct values, the probability of exactly one permutation of these three distinct numbers forming a strictly increasing sequence is

  

  Multiplying these yields

Both methods yield the same probability,

$$\frac{5}{54},,$

which confirms the result.

Why the probability that all three rolls are distinct is (5/6 × 4/6)

The first roll can be anything. For the second roll to be different from the first, there are 5 valid faces (out of 6) remaining. For the third roll to differ from both the first and second, there are 4 valid faces remaining. Since each roll is independent and has six equally likely outcomes, you multiply these independent probabilities to get

Why the conditional probability of strictly increasing order among three distinct values is 1/6

Once you know three dice results are all different, you can list the values in ascending order, descending order, or any of the other permutations. There are 3! = 6 ways to arrange three distinct numbers. Exactly one of these permutations is strictly increasing. Thus the probability is 1/6.

Practical verification via simulation

It can be helpful to write a quick simulation in Python to confirm:

import random

N = 10_000_000
count_increasing = 0

for _ in range(N):
    rolls = [random.randint(1,6), random.randint(1,6), random.randint(1,6)]
    if rolls[0] < rolls[1] < rolls[2]:
        count_increasing += 1

empirical_probability = count_increasing / N
print("Empirical Probability:", empirical_probability)

If you run this with a sufficiently large N, you should see the approximate result converge near 5/54, which is approximately 0.09259 (about 9.259%).

What would happen if the dice were not fair?

If each die roll had a different probability distribution (for instance, if some faces were more likely than others), the main change would be in how you compute the probability of each face appearing. The concept of “strictly increasing” remains, but you no longer can assume each outcome has probability 1/6. Instead, you would need to calculate:

• The probability of a specific triplet (x, y, z) given the biased distributions.

• Sum these probabilities over all triplets x < y < z.

  

How do we extend this problem to more rolls, say four or five dice throws?

For more than three dice, the same logic applies, but the counting can be generalized. If you roll n dice, the total outcomes are

$$6^n,.$

The number of strictly increasing sequences is equivalent to choosing n distinct numbers out of 6, then ordering them in exactly one way. The number of ways to choose these n distinct faces is

$$\binom{6}{n},.$

Hence, the probability of strictly increasing order is

$$\frac{\binom{6}{n}}{6^n},.$

For n > 6, the probability is zero, because you cannot have n distinct faces when only six faces exist.

How does this analysis change for non-strictly increasing sequences (allowing repeats)?

If repeats are allowed in the sense of non-decreasing (i.e., each roll is greater than or equal to the previous roll), you can treat it as a stars-and-bars combinatorial problem. You would be effectively looking for the number of solutions to

with each x in {1,2,3,4,5,6}. Another way is to think of it as the number of ways to pick 3 values in ascending order, allowing repeats. The formula typically involves combinations with repetition. That count is

$$\binom{6 + 3 - 1}{3} = \binom{8}{3} = 56,.$

Then you would divide 56 by 6^3 = 216 for the probability, giving 56/216 = 14/54 = 7/27. This is a distinct scenario from the strictly increasing one.

Could we solve it by direct enumeration?

Yes, for three dice it’s small enough to enumerate all 216 outcomes by systematically listing them and checking which ones meet the strictly increasing condition. For each triple (a, b, c) with a, b, c in {1,2,3,4,5,6}, we count how many satisfy a < b < c. We should find 20 such sequences, leading to the probability 20/216 = 5/54.

What are typical pitfalls or mistakes in solving this problem?

One mistake is forgetting that the total number of ways to order three distinct numbers is 3!, which can lead to an incorrect fraction for the conditional probability. Another common error is forgetting that repeated numbers make strict inequality impossible, leading to incorrect counting of the favorable cases. Additionally, using the 3 distinct number approach but not multiplying it by the correct fraction for the strictly increasing arrangement is a common slip.

What real-world scenarios might this concept relate to?

Even though rolling dice is a straightforward scenario, the concept of strictly increasing sequences can appear in:

• Timing of network packets arriving in strictly increasing timestamps.

• Quality control where measurements must show a strictly increasing pattern in certain processes (though real-world distributions may not be uniform).

• Various discrete event simulations where certain states must be strictly ascending to qualify as a success state.

In these cases, the uniform distribution assumption might not hold, so you would adapt the approach by weighting each possible outcome according to its probability distribution and summing the probabilities of all strictly increasing outcomes.

---

Below are additional follow-up questions

What if you want to ensure a strictly increasing sequence at least once after multiple sets of three rolls?

One might ask: if you roll the dice in sets of three, say M independent times, and you want to find the probability that you get at least one strictly increasing triplet among these M sets, how would you approach that?

To solve this, you can use the complement rule. First, note that the probability of getting a strictly increasing sequence in a single triple is 5/54. The probability of not getting a strictly increasing sequence in that triple is 1 – (5/54) = 49/54. If you roll M separate and independent sets of three dice, the probability of never obtaining a strictly increasing triplet is (49/54)^M. Hence, the probability of getting at least one strictly increasing triple in M sets is

A subtle real-world issue might arise if the M sets of rolls are not truly independent. For example, if the same physical die is used across sets and is biased in a way that changes over time, or if you do not properly randomize, then this formula may underestimate or overestimate the probability. You would need to consider correlation between different sets of rolls in a practical scenario.

What if each die has a different number of faces or labeling?

Sometimes dice may not be standard 1-to-6 dice. You might have dice labeled with unusual numbers, or they could even have a different number of sides (for instance, an 8-sided or 10-sided die). For strictly increasing outcomes, the key is to account for the exact set of possible faces for each die and then enumerate or calculate the probability of all valid triples (a, b, c) where a < b < c based on the distribution of faces.

For three dice with distinct sets of faces A, B, and C, the total number of outcomes is |A| × |B| × |C|. You would enumerate all possible triples (a in A, b in B, c in C) and check how many satisfy a < b < c. If the dice are fair, each triple is equally likely, so the probability of a strictly increasing sequence is:

A practical pitfall might be forgetting that each die can have a different face set or different probabilities for each face. You must account for each die’s unique configuration carefully, rather than assume a uniform distribution over identical faces.

How do we handle incomplete information about the rolls?

Imagine a scenario where you rolled three dice but only observed two results, or you know that two of the dice landed on odd faces but not exactly which odd faces. In such partial-observation cases, you need a conditional probability approach:

1. Determine what partial information you have (e.g., “the first die is known to be 2, the second die is unknown, the third is known to be greater than 3”).

2. Enumerate all possible combinations of the unknown rolls consistent with the partial observations.

3. Among those valid combinations, count how many satisfy a strictly increasing pattern.

4. Divide by the total number of valid combinations.

A subtle point here is that partial observations might alter the probabilities if the partial observation is itself correlated with the outcome. For instance, if you somehow suspect that not seeing the second die fully is more likely if that die shows a high number, you would need a Bayesian updating mechanism to incorporate that prior knowledge. In an interview, clarifying how partial information arises and how it influences the probability distribution is crucial.

How does the result generalize to random draws from a continuous distribution?

If instead of rolling dice, you draw three numbers independently from a continuous distribution (like Uniform(0, 1)), the probability of those three draws being strictly increasing is 1/6. More precisely, for n draws from a continuous distribution, the probability that the sample is in strictly ascending order is 1/n!. For the discrete dice case, we have 5/54 because there is only a 6-element sample space for each draw, and the outcomes can coincide. In the continuous case, the probability of duplicates is effectively zero, so you get a simpler ratio.

A subtlety is that if the continuous distribution can generate identical values with some probability (e.g., a mixture with discrete spikes), then the duplicates are no longer negligible, and the strict inequality logic changes. You would then have to split the probability space into a purely continuous portion and the point masses, carefully analyzing how often duplicates arise.

What happens if we consider a different inequality condition, like “a ≤ b ≤ c” (non-strict) and we also require that at least one inequality be strict?

In some practical scenarios, you might allow the dice results to be non-decreasing but also require that not all three be the same. If you want to ensure it’s not all equal while still being in ascending order, you can think of it as:

• Total ways to have a ≤ b ≤ c, which includes duplicates.

• Subtract the single pattern where a = b = c, because that’s entirely equal.

• The remainder is the set of outcomes that are at least weakly increasing with at least one strict inequality.

The total count for non-decreasing triples from a discrete set of size 6 is computed by combinations with repetition:

There are 6 ways for all three numbers to be the same (1,1,1), (2,2,2), ..., (6,6,6). So the new total is 56 - 6 = 50. The probability would then be 50/216. One subtlety here is double-checking if the problem’s condition means “not all three are equal” or “at least one strict inequality.” Always confirm the exact logical requirement for the inequality to avoid off-by-one or miscounting errors.

What if there is a time element where each die roll could be invalid if it was too slow or outside a certain time window?

One could imagine a scenario where each roll must happen quickly, or it’s discarded. This might create a truncated dataset where only some fraction of the rolls are deemed “valid.” Now, your probability calculation must be updated to reflect that you only consider successful valid rolls. For instance:

1. Each roll has a probability p of being valid (rolled in time), and 1 − p of being invalid (discarded).

2. If any one of the three is discarded, you can’t form a valid triple.

3. Among the valid sets, you then look for strictly increasing sequences.

Hence, the total valid sets form a binomial-like distribution for each roll’s success or failure. The probability that all three dice yield valid results is p^3, and within those valid sets, the fraction that is strictly increasing is 5/54 (assuming normal fair dice). The final probability is p^3 × (5/54). A subtlety might be that if the probability p depends on the face value shown (e.g., maybe rolling a 6 is quick to observe, rolling a 1 is slow to pick up), that could introduce complex correlations between validity and face outcome. You would need a more intricate model in that case.

What if the dice can land off the table or get re-rolled under certain rules?

Sometimes, if the dice land off the table, that roll is voided, and you roll again. This is an example of a conditional sampling process. If you only keep outcomes that land on the table, you need to figure out the probability distribution of the valid “on-table” faces. Potentially, a certain face might be more prone to rolling off the table in real life if the physical dice are unbalanced or if the player rolls them in a certain way. The mathematics then shifts from a pure theoretical 1/6 per face to a conditional distribution for on-table results. Once you know that distribution, you can re-derive the probability of strictly increasing sequences under that new distribution. A subtlety arises if the off-table event is not uniform across faces. In an interview, clarifying these real-world complexities is often a sign of deeper understanding.

How can we leverage dynamic programming if the number of rolls increases?

For a large number of rolls, direct enumeration can become unwieldy. Although for dice with only six faces, you could still theoretically use counting formulas, you might want a dynamic programming approach to handle constraints like “no partial repeats,” “strictly increasing,” and so on. A dynamic programming approach would consider states defined by how many rolls have been made and the last roll’s value, and it would accumulate the number of valid strictly increasing sequences up to that point.

For instance, let DP(k, v) be the number of ways to have a strictly increasing sequence of length k that ends with value v. Then you can sum over possible preceding values that are strictly less than v for the (k − 1)-roll sequence. This can be generalized for more complex constraints, such as skipping certain faces or having limited face availability. A subtlety is that you must set appropriate boundary conditions, like DP(1, v) = 1 for v in {1, ..., 6}, and carefully handle transitions to avoid counting invalid sequences.

How to approach hypothesis testing for “the dice yields a strictly increasing sequence more often than expected”?

In certain settings, someone might suspect the dice or the way the dice are rolled is rigged to produce an unusually large number of strictly increasing outcomes. If you want to test this hypothesis:

1. Null hypothesis: The dice are fair, so the probability of a strictly increasing triple is 5/54.

2. Collect a sample of N triples of rolls.

3. Count how many strictly increasing triples occurred.

4. Compare to the expected value under the null (N × 5/54). Use a binomial or chi-square test to see if the discrepancy is statistically significant.

A subtle real-world issue is ensuring independence in your sample. If the person rolling the dice changes their technique mid-way, or if there is a hidden systematic pattern (like certain times of day they roll differently), the binomial assumption might be violated. You might need to model correlation effects or repeated measures.

How do marginal probabilities compare for each position in a strictly increasing sequence?

You might be curious about the distribution of the first, second, and third die values given that they form a strictly increasing triple. For instance, which value is most common for the first die under a strictly increasing constraint? One can deduce it by counting how many triples start with 1, how many with 2, etc., all with strictly increasing properties. For example:

• Start with 1: The second can be 2, 3, 4, 5, or 6, and the third can be anything bigger still, leading to a certain sub-count.

• Start with 2: The second can be 3, 4, 5, or 6, and so on.

By enumerating or using combinatorial logic, you find a distribution of the first-die value under the condition that the entire triple is strictly increasing. A subtlety is that for real dice, if the outcomes are correlated (e.g., the way you roll the second die depends on the first), this distribution might differ from the purely combinatorial approach.

How to modify the probability if there is a “reroll chance” after each roll?

Suppose you have a game rule allowing you to reroll the second or third die if you don’t like its value, trying to get a strictly increasing sequence. This changes the probability drastically, because you now have strategic rerolls that can eliminate certain undesired outcomes. You might approach it by enumerating all possible outcomes of the first roll, the reroll policies for the second, and so on. For instance:

1. Roll the first die (no choice but to keep).

2. Roll the second die; if it’s not bigger than the first, maybe you choose to reroll once more.

3. Roll the third die; if it’s not bigger than the second, maybe you reroll.

The probability of success becomes the result of a tree of probabilities weighted by the chance of each outcome and the policy you use for deciding to reroll or keep. A subtlety here is the existence of a finite number of rerolls. If you have only one reroll, you have to decide carefully whether it’s better used on the second or third die, which can lead to a more complex decision-making process.