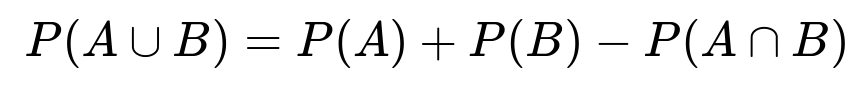ML Interview Q Series: Probability of Concurrent Head/Tail Runs in Tosses using Inclusion-Exclusion.

Browse all the Probability Interview Questions here.

A fair coin is tossed 20 times. The probability of getting three or more heads in a row is 0.7870, and the probability of getting three or more heads in a row or three or more tails in a row is 0.9791. What is the probability of getting three or more heads in a row and three or more tails in a row?

Short Compact solution

Using the principle of inclusion-exclusion for events A (three or more heads in a row) and B (three or more tails in a row), we have:

P(A) = 0.7870 P(B) = 0.7870 P(A ∪ B) = 0.9791

Hence,

P(A ∩ B) = 0.7870 + 0.7870 − 0.9791 = 0.6049

Comprehensive Explanation

Inclusion-Exclusion Principle

A key relationship in probability theory is that the probability of the union of two events A and B can be expressed as:

This formula tells us that if we want to find P(A ∩ B), we can rearrange to get:

P(A ∩ B) = P(A) + P(B) − P(A ∪ B)

Here:

• A is the event “three or more heads in a row in 20 tosses.” • B is the event “three or more tails in a row in 20 tosses.”

We are given: • P(A) = 0.7870 • P(B) = 0.7870 • P(A ∪ B) = 0.9791

Thus,

P(A ∩ B) = 0.7870 + 0.7870 − 0.9791 = 0.6049

This implies there is a 0.6049 probability that in 20 tosses, you will see at least one run of three heads and at least one run of three tails.

Why the Inclusion-Exclusion Principle Works Here

The reasoning is straightforward if we imagine drawing a Venn diagram with two overlapping circles: one circle for the event A (three or more heads in a row) and the other for B (three or more tails in a row). If we simply add P(A) + P(B), we count the intersection region (the outcomes that have both three heads in a row and three tails in a row) twice, so we subtract P(A ∪ B) from that sum once to correct for double counting.

Interpretation

A probability of around 0.60 for getting both a three-heads streak and a three-tails streak underscores that in 20 fair coin flips, it is quite common to see both phenomena occur. Because the coin is fair, each toss is equally likely to be heads or tails, so the chance of seeing both patterns is significantly high once you have 20 trials.

Practical or Computational Approaches

1. Markov Chain or State Machine: One could build a Markov chain whose states encode how many heads or tails have just appeared in a row and calculate P(A), P(B), and P(A ∩ B) exactly. This is usually done in texts covering runs in Bernoulli processes.

2. Dynamic Programming: Another exact approach is to use dynamic programming to keep track of the probability of each possible “run state” at each step. The approach counts how many ways (or the probability) that certain run constraints can be satisfied.

3. Simulation: A Monte Carlo simulation can be performed to verify or approximate these probabilities. Simply simulate 20 coin flips many times (e.g. a few million) and estimate the probabilities of A, B, and their union and intersection.

Follow-up Question: Why might these events overlap so much?

When we say “these events overlap a lot,” we mean that P(A ∩ B) is fairly large. Intuitively, once you have 20 flips, it is likely to see a short run of heads at some point and a short run of tails at some point. Runs of heads and runs of tails do not necessarily exclude each other; in fact, multiple transitions between heads and tails across 20 flips often allow both runs to appear.

Follow-up Question: How could we confirm the correctness of these probabilities?

One could create a brute-force enumeration of all 2^20 possible outcomes of 20 coin tosses. For each outcome (string of length 20 composed of H or T):

• Check if it contains HHH. • Check if it contains TTT.

Then tally the frequencies of outcomes that satisfy A, B, and both A and B. From that count, you get the exact probabilities by dividing by 2^20. This method, however, requires enumerating 1,048,576 possibilities, which is feasible for a computer. A smaller-scale dynamic programming or Markov chain can also confirm these exact probabilities without enumerating all possibilities.

Follow-up Question: If the coin were biased, how would the probability change?

If the coin has probability p of landing heads and 1 − p of landing tails, the events A (run of three heads) and B (run of three tails) become more or less likely depending on how p deviates from 0.5:

• If p >> 0.5, runs of heads become much more likely, and runs of tails become less likely (so A is more likely, B is less likely). • If p << 0.5, the reverse happens.

One could adapt either the state-based Markov chain or dynamic programming approach to handle the biased case, but the closed-form answers often become more complicated. Simulation is a straightforward way to empirically approximate these probabilities for a biased coin.

Follow-up Question: How does run probability analysis appear in real machine learning or data science work?

Patterns of runs arise in time-series analysis, reliability analysis, and anomaly detection. For instance:

• Quality control: Checking for runs of defective items in a production line. • Financial modeling: Looking at runs of gains or losses in stock price data (though those distributions are not necessarily i.i.d.). • A/B testing analytics: Observing consecutive visitor responses (e.g., sign-ups vs. non sign-ups) to see if performance is consistent or if there’s a run that indicates a particular user segment might be responding differently.

In machine learning contexts, runs could manifest in sequential data patterns or in Markov chain Monte Carlo processes, where you might be concerned about consecutive samples falling into certain states. Understanding the probabilities of these runs can be important for interpreting model outputs or diagnosing unexpected sequence behavior.

Follow-up Question: Could you show a quick Python simulation?

Below is a simple Python code snippet to approximate these probabilities. It might not match exactly the given values for small sample sizes but will converge with a large number of simulations:

import random

def has_three_in_a_row(sequence, char):
    # Checks if char (e.g., 'H') appears three times consecutively in sequence
    for i in range(len(sequence) - 2):
        if sequence[i] == char and sequence[i+1] == char and sequence[i+2] == char:
            return True
    return False

N = 10_000_00  # Number of simulations
count_A = 0
count_B = 0
count_AB = 0

for _ in range(N):
    flips = [random.choice(['H', 'T']) for _ in range(20)]
    eventA = has_three_in_a_row(flips, 'H')  # A: 3 heads in a row
    eventB = has_three_in_a_row(flips, 'T')  # B: 3 tails in a row

    if eventA:
        count_A += 1
    if eventB:
        count_B += 1
    if eventA and eventB:
        count_AB += 1

pA = count_A / N
pB = count_B / N
pAB = count_AB / N
pA_union_B = pA + pB - pAB

print("P(A):", pA)
print("P(B):", pB)
print("P(A ∩ B):", pAB)
print("P(A ∪ B):", pA_union_B)

As you increase N, these estimates will tend to hover around the values in the problem statement (0.787 for P(A), 0.787 for P(B), etc.), verifying the theoretical answer via simulation.

Below are additional follow-up questions

What if we want the probability of exactly one event happening (three heads in a row but not three tails in a row, or vice versa)?

An important variation is to find the probability of “A but not B” or “B but not A.” For instance, if A is the event of getting at least one run of three heads, and B is the event of getting at least one run of three tails, then:

• Probability of only A (i.e., A and not B) can be expressed as P(A) − P(A ∩ B). • Probability of only B (i.e., B and not A) can be similarly expressed as P(B) − P(A ∩ B).

To see why, note that P(A) includes all outcomes where three heads appear (whether or not three tails also appear). If we want strictly A and not B, we remove the cases where B also occurs. The major pitfall here is to forget that events can overlap significantly, leading to an incorrect assumption that simply subtracting from 1 gives the probability of the other event not happening. Instead, we must precisely isolate only those outcomes that belong exclusively to one event.

In real-world testing, you might want to identify sequences that show a run of a particular type (e.g., repeated positives in a quality control test) but not the other (repeated negatives). Paying attention to overlaps is crucial because runs of different categories can occur in the same sequence.

Could having many short runs reduce the chance of both events happening?

One might wonder if frequent switching between heads and tails (i.e., many short runs but never reaching three in a row) affects the intersection probability. In principle, if the coin sequence toggles very frequently, you might never get three consecutive heads or three consecutive tails, thus missing both A and B entirely. However, if you do get three consecutive heads at some time, that does not necessarily preclude you from also getting three consecutive tails later (or earlier) in the same sequence of 20 flips.

The subtlety: frequent toggling reduces the chance of even a single run of length 3 (because you keep “breaking” the streak). But once you do form a run of length 3 in one category, toggling does not necessarily disrupt the other category from eventually forming its own run, especially if there are enough flips left. A pitfall is to assume that frequent toggling either “guarantees” both runs or “prevents” both runs, when in fact the effect is more nuanced and depends on the overall distribution of heads and tails across the 20 flips.

How would overlapping runs (like HHHH) factor into the counting of three in a row?

Overlapping runs can sometimes complicate how we think about counting. For example, HHHH is effectively two distinct occurrences of “three heads in a row” (the first three heads are indices 1,2,3 and the second three heads are indices 2,3,4). However, for the event A (having at least one run of three heads), it only matters if at least one run of length 3 is present. The difference between a single run of length 3 versus multiple runs of length 3 does not affect the event A in a yes/no sense—both scenarios simply satisfy A.

In practice, an important pitfall is to overcount or double-count runs. For instance, while enumerating or checking by code, if you track every occurrence of HHH, you could incorrectly assign more weight to sequences that have multiple such runs unless you carefully structure your logic. In the probability calculation for “at least one run,” we just need a binary indicator (true/false). Overlapping runs do not inflate or reduce the probability beyond that of simply having at least one run, so it’s essential to keep the event definition consistent.

What if we need to account for longer runs (like four or more heads or tails in a row) and compare them to runs of length three?

Sometimes, interviewers may extend the question to scenarios like “at least one run of four heads” (or five or six) versus “at least one run of three heads.” The pitfall is that as you change the run length requirement, you can’t directly rely on the same numeric results or intuitive overlap. For example, the probability of at least one run of four heads is less than that for at least one run of three heads, so the intersection of “four heads in a row” and “three tails in a row” might be quite different.

Moreover, a sequence that has a run of four heads also automatically has at least one run of three heads (embedded within the four). But the reverse is not always true (three heads doesn’t necessarily mean four heads). This nested relationship can create logical dependencies that require more careful state-based analysis. If you simply try to apply the same 0.7870 or 0.9791 numbers, you would be making a significant assumption error because those probabilities are specifically for three consecutive heads/tails.

Could we extend the scenario to more than two events, such as “three or more heads in a row,” “three or more tails in a row,” and “five or more heads total”?

In an interview context, it’s common to see expansions to multiple events. For instance, you might want:

• A = “three or more heads in a row” • B = “three or more tails in a row” • C = “five or more heads total”

Now you have three events, and you might be interested in P(A ∪ B ∪ C) or some intersection like P(A ∩ C). The challenge increases because the union of three events formula is more complicated:

P(A ∪ B ∪ C) = P(A) + P(B) + P(C) − P(A ∩ B) − P(A ∩ C) − P(B ∩ C) + P(A ∩ B ∩ C)

A big pitfall is to forget to add back in the triple intersection. People often overcount or undercount because they either miss the final correction term or do not properly calculate each pairwise intersection. Furthermore, these events might not be independent or even “weakly dependent,” so you can’t simply multiply or do naive approximations without carefully analyzing all overlaps.

What is the role of negative correlation or dependence between runs of heads and runs of tails?

Even though events A and B can occur together, they are not entirely independent. One might suspect that having a run of three heads early in a sequence could reduce the time or “opportunity” to get a run of tails of length three, but with 20 flips, there is still ample room for multiple transitions.

In advanced probability, the term “dependence” refers to whether the occurrence of one event influences the probability of the other. For short sequences (e.g., only five flips), A and B would be nearly mutually exclusive because it’s hard to fit both runs of three in such a small sequence. But as the number of flips grows, the events overlap more frequently, indicating less negative correlation. Recognizing how correlation between runs arises is crucial in real-world tasks like analyzing reliability data, where you might suspect certain types of failures (analogous to heads runs) might reduce or increase the likelihood of other failures (tails runs) within the same timeframe.

How do we handle boundary cases like fewer tosses (e.g., 3 or 4 tosses)?

If the coin is tossed fewer than 3 times, obviously neither event A nor event B can occur, so probabilities for both would be 0. For 3 tosses exactly, you could have exactly one run of three heads or three tails if all flips are the same, so:

• Probability of three heads in a row is (1/2)^3 = 1/8.

• Probability of three tails in a row is also 1/8.

• Probability of A ∩ B in exactly 3 flips is 0 because you can’t have both three heads and three tails in only 3 tosses.

If you have 4 tosses, the scenarios are a bit more involved, but the maximum number of distinct runs of length 3 is still only 2 overlapping runs (e.g., HHHH or TTTT). As you move from small sequences (3, 4, 5 flips) up to 20 flips, the intersection probability transitions from 0 to a more substantial number. The pitfall is to assume the pattern for 20 flips generalizes in a straightforward way to a smaller number of flips; each situation must be calculated or simulated carefully based on the exact sequence length.

How might real-world data deviate from the idealized model of fair, independent coin flips?

Real data often violates the assumptions of:

1. Independence: In many real processes, consecutive events might be correlated (e.g., system performance can degrade over time, making consecutive events more likely to be failures).

2. Identical distribution: The probability of heads vs. tails might change over time. For instance, in a sensor reading scenario, the chance of reading a “high” (analogous to heads) could drift due to environmental changes.

3. Exact 50-50 chance: Many real processes have underlying probabilities p different from 0.5.

These assumptions, if broken, can drastically alter the probability of seeing specific runs. If events are positively autocorrelated (i.e., a run of heads makes future heads more likely), then runs become even more probable. The major pitfall in data science is applying theoretical formulas derived from fair, independent coin flips to real data that does not meet those conditions. Always test or estimate the actual autocorrelation structure before applying run-based probability formulas.

How can partial-run boundaries (like HHTHH at the boundary of a set of flips) affect your counting in streaming data?

In streaming data contexts, you might continuously observe data points and want to detect runs in rolling windows of length 20. A subtle pitfall occurs if you treat each new 20-length window in isolation without remembering that some portion of a run might have “started” in the previous window. For instance, if the 20 flips window ended with HHH, your next window might start with that same triple, effectively merging with additional heads in the subsequent flips.

In practice, you’d maintain state between windows—for example, how many heads in a row had occurred at the tail end of the previous window. If you reset on each new window, you might underestimate the probability of runs because you are artificially truncating them. So in continuous monitoring systems (like network packet analysis, quality control lines, or event streams in IoT data), you need to carefully handle boundary overlaps when computing probabilities of runs across windows.