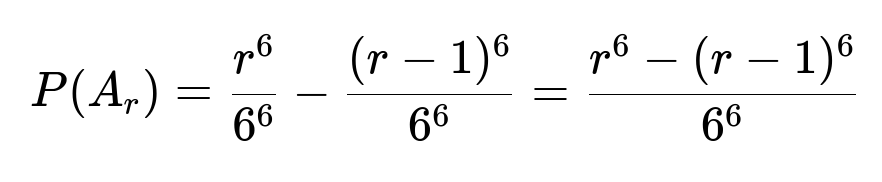ML Interview Q Series: Probability of Maximum Value in Six Die Rolls via Cumulative Distribution

Browse all the Probability Interview Questions here.

A fair die is rolled six times. What is the probability that the largest number rolled is r for r = 1,...,6?

Short Compact solution

Define A_r to be the event that the maximum of the six rolls is r. Observe that the total number of possible outcomes in six rolls of a fair die is 6⁶ (each roll can independently be from 1 to 6). Let B_k be the event that all six outcomes are at most k. Hence, P(B_k) = k⁶ / 6⁶. Then A_r can be interpreted as the event that all six rolls are at most r, but not all six at most (r-1). Therefore,

A_r = B_r \ B_r-1,

leading to

P(A_r) = P(B_r) - P(B_r-1) = (r⁶/6⁶) - ((r-1)⁶/6⁶) = [r⁶ - (r-1)⁶] / 6⁶.

An alternative derivation is to consider j of the rolls exactly equal to r and the remaining (6 - j) rolls to be strictly below r. Summing over j from 1 to 6 (since we must have at least one roll equal to r for the maximum to be r) gives the same result.

Comprehensive Explanation

When we roll a fair six-sided die six times, each outcome is a sequence of length 6, where each element can be an integer from 1 to 6. Thus, there are 6⁶ equally likely ways to roll the die six times.

To find the probability that the largest number observed is exactly r, we use two main methods:

Difference of Cumulative Counts Approach

We introduce:

B_k = "All six dice show a value from the set {1, 2, ..., k}."

Because there are k choices per roll if the dice values must be at most k, the number of sequences that satisfy B_k is k⁶. So:

P(B_k) = (k⁶) / (6⁶).

Now, A_r = "The maximum value in the six rolls is r." This is the same as saying "All six rolls are at most r, and at least one of them is equal to r." Equivalently, A_r = B_r \ B_r-1, because B_r is the event that the rolls are all ≤ r, and B_r-1 is the event that the rolls are all ≤ r-1, so removing B_r-1 from B_r leaves exactly the set of outcomes whose largest number is r (none larger than r, but at least one r).

Hence:

Here:

• r⁶ is the number of ways to roll six dice with faces in {1, 2, ..., r}.

• (r-1)⁶ is the number of ways to roll six dice with faces in {1, 2, ..., r-1}.

• 6⁶ is the total number of equally likely outcomes for six rolls.

Summation / Binomial Approach

Alternatively, we can think of A_r by enumerating the ways in which the largest die can be r:

• Suppose exactly j of the dice show r (j ≥ 1), and the other (6 - j) dice each show a value from 1 to (r-1).

• The probability that any particular sequence of j dice being r and the other (6 - j) being below r is (1/6)^j · ((r-1)/6)^{(6 - j)}.

• The number of ways to choose which j dice show r is C(6, j).

• Summing over j from 1 to 6 gives:

This summation can be shown to be identical to [r⁶ - (r-1)⁶]/6⁶ by the binomial expansion of r⁶ - (r-1)⁶.

Edge Cases and Basic Checks

1. When r = 1, the largest number is 1 if and only if all dice are 1. Then (1⁶ - 0⁶) / 6⁶ = 1/6⁶.

2. When r = 6, the probability is 6⁶/6⁶ - 5⁶/6⁶ = 1 - (5⁶/6⁶).

These edge cases match intuition: r=1 means all dice must be 1 (a very small probability), r=6 means at least one 6 occurs.

Example Computation in Python

from math import comb

def prob_largest_r(r):
    # Using difference approach
    return (r**6 - (r-1)**6) / (6**6)

# Alternatively using binomial approach
def prob_largest_r_binomial(r):
    total = 0
    for j in range(1, 7):
        ways = comb(6, j)
        p_r = (1/6)**j
        p_less = ((r-1)/6)**(6-j)
        total += ways * p_r * p_less
    return total

for r in range(1, 7):
    print("r =", r, "=>", prob_largest_r(r), " / binomial =>", prob_largest_r_binomial(r))

Either approach returns the same probabilities.

Possible Follow-up Questions

If an interviewer asks: "How do we verify that these probabilities sum to 1?"

We note that the events A₁, A₂, …, A₆ partition the entire sample space. Each sequence of six rolls has a unique maximum (it must be exactly one of 1, 2, 3, 4, 5, or 6). Hence,

P(A₁) + P(A₂) + ... + P(A₆) = 1.

Mathematically, from the difference expression:

Σ[r=1..6] (r⁶/6⁶ - (r-1)⁶/6⁶) = (1⁶ - 0⁶ + 2⁶ - 1⁶ + ... + 6⁶ - 5⁶) / 6⁶ = (6⁶ - 0⁶) / 6⁶ = 1.

If asked: "How can we extend this to dice with n sides or more than six rolls?"

For an n-sided fair die rolled m times, the same reasoning applies, with total outcomes n^m. The probability that the largest roll is r (for r = 1, …, n) becomes:

Largest number ≤ r means B_r has r^m outcomes. Then:

P(A_r) = [r^m - (r-1)^m] / n^m,

or via the combinatorial approach:

P(A_r) = Σ[j=1..m] C(m, j) (1/n)^j ((r-1)/n)^(m-j).

If asked: "What is the expected value of the largest roll in six throws of a fair die?"

The expected largest roll L is:

E[L] = Σ[r=1..6] r × P(A_r).

This quantity can be computed directly by plugging in the probabilities found. Numerically, it is often around 4.45 for six rolls of a fair six-sided die.

If asked: "What if the die is biased so that each face i has probability p_i?"

Then the direct counting method (r⁶ etc.) no longer applies because the total number of sequences is still 6⁶, but they are not equally likely. Instead, we sum over the probabilities:

Let the largest roll be r. This means each face is at most r, at least one face is exactly r, and we use:

P(A_r) = Probability(all rolls ≤ r) - Probability(all rolls ≤ r-1).

But "Probability(all rolls ≤ r)" is [p(1) + p(2) + ... + p(r)]⁶. So:

P(A_r) = [p(1) + ... + p(r)]⁶ - [p(1) + ... + p(r-1)]⁶.

One must be careful since the p₁, p₂, …, p₆ might not all be 1/6.

If asked: "How can you use these probabilities in a real application, like gaming or simulation?"

In many games, the distribution of the maximum roll determines chances of success (for instance, if you roll multiple dice and only the largest matters). One can compute expected payoffs, or the chance of exceeding a certain threshold, by knowing P(A_r). Similarly, in simulations, checking if the maximum surpasses a boundary is relevant in bounding extreme events.

All these points demonstrate how the straightforward idea of "largest number among multiple throws" can be systematically tackled by either:

1. Subtraction of cumulative event probabilities for "values not exceeding r."

2. A combinatorial sum capturing the possibility of having exactly j dice land on r and the rest below r.

Below are additional follow-up questions

If an interviewer asks: "How would you find the probability that exactly k distinct faces appear among the six rolls, and how is that related to the distribution of the largest roll?"

One might wonder how often we see exactly k distinct numbers in 6 throws and how that event might constrain the largest roll. To approach this:

• First, recognize that “exactly k distinct faces” is a more general event encompassing multiple possible largest values.

• We can count the number of ways to choose which k faces appear, assign them among the six positions, and ensure all chosen faces occur at least once. This involves Stirling numbers of the second kind or the inclusion-exclusion principle.

• If we want to incorporate the largest face condition, we can fix the largest face to be r and then count how many distinct faces are used among the remaining (r-1) possible faces plus the forced presence of r. That is a more intricate inclusion-exclusion question.

• Potential pitfalls:

  1. Overcounting if we do not carefully enforce “exactly k distinct faces.”

  2. Failing to account for the forced presence of r if we want the largest face to be r.

  3. The complexity can grow quickly, so it is easy to introduce small miscounts that distort the result.

If an interviewer asks: "How do we calculate the probability of the largest roll being at least r, and how might that be more useful than finding exactly r?"

Sometimes, we care about “at least r” rather than “exactly r.” For instance, “What is the chance of rolling at least one 5 or 6 in six throws?”

• We define A_≥r = “The largest roll is at least r.”

• A direct approach is: P(A_≥r) = 1 - P(all rolls < r). Because if the largest is not at least r, then all rolls must be ≤ (r-1).

• So, P(A_≥r) = 1 - ((r-1)/6)⁶.

• Pitfall: Overlaps might occur if we try to do the complement incorrectly (for example, mixing up “all rolls < r” with “all rolls ≤ r”).

This is typically simpler than “exactly r” because we avoid enumerating each maximal outcome in detail and can just exploit the complement.

If an interviewer asks: "What is the probability that the largest roll appears exactly m times (for example, we want the largest face r to appear exactly 2 times), and how can this be computed in tandem with P(A_r)?"

This question combines the concept of having a largest roll r with a specific frequency of r:

1. We already know P(A_r) is the probability the largest value is r.

2. Within that event, we might want the largest value r to appear exactly m times.

To drill down:

• First ensure at least one r occurs (so the max can be r). Then we specifically count the number of ways for exactly m dice to show r.

• The other (6 - m) dice must be strictly from {1, 2, ..., r-1}, but none of those (6 - m) dice can be r (otherwise we exceed m occurrences of r).

• We can use combinations to choose which m positions are r, multiply by the number of ways to fill the remaining positions with faces < r, and then normalize by 6⁶.

Pitfalls include forgetting to exclude the possibility of a larger face or not ensuring that if m < 6, we still have no dice face > r.

If an interviewer asks: "How would you handle dependent dice rolls or real-world scenarios where the outcomes of the rolls are not truly independent?"

Real dice rolls in an ideal environment are typically modeled as independent. But some real-world situations (or contrived problems) might introduce correlations among the rolls:

• For instance, consider a scenario where we suspect a mechanical or physical dependency: if one roll is high, maybe the next is more likely to be low due to how the dice are tossed.

• In that case, the standard counting approach (r⁶ out of 6⁶) doesn’t apply directly because it relies on independence to ensure the 6⁶ equally likely outcomes.

• We would need the joint distribution of all six rolls. The “largest roll = r” event would then be integrated (or summed) over this joint distribution.

• Potential pitfalls:

  1. Assuming independence incorrectly, leading to flawed results.

  2. Attempting to apply the simple formula (r⁶ / 6⁶) when the probabilities of each combination are not uniform.

If an interviewer asks: "How do we simulate rolling a die six times, record only the largest result, and use that to estimate P(A_r) empirically? What mistakes do people often make in simulation-based estimates?"

A simulation-based approach can empirically approximate P(A_r):

1. Generate a large number of trials, each with six i.i.d. uniform(1..6) draws.

2. Track the maximum of each trial’s six draws.

3. Estimate P(A_r) by the frequency of trials whose maximum is r.

Common mistakes:

• Not using enough trials, leading to high variance estimates or confidence intervals that are too wide.

• Mixing up the index of the largest die face with the face value (for instance, confusing the position of the largest roll with its numeric value).

• Failing to reset random seeds or incorrectly collecting data, which can skew results or hamper reproducibility.

If an interviewer asks: "How do we extend or adapt these ideas if dice have faces that are not integer-labeled (e.g., a specialized gaming die with arbitrary symbols)?"

In many custom dice or specialized gaming scenarios, each side might have a different label or symbol, possibly not even numeric. To adapt:

• The notion of 'largest roll' might be replaced with 'the highest-ranked symbol' if we can define a ranking or ordering among the symbols.

• We must identify an ordering from least to greatest among those faces. Once established, the count of “faces ≤ r” can be used similarly.

• Potential pitfalls:

  1. If no clear total ordering exists (some games may have multiple categories rather than a single rank), the concept of “largest” might be ambiguous.

  2. If each face does not share equal probability, the uniform count approach breaks down, and we must rely on the sum of probabilities for faces up to “r” instead of counting them as consecutive integers.

If an interviewer asks: "How does the concept of 'the largest of n random variables' generalize to continuous distributions, and what parallels exist with the discrete dice roll approach?"

Though dice are discrete, there is a continuous analogue:

• For continuous i.i.d. random variables X₁, X₂, ..., X_n with cumulative distribution function F(x), the probability the maximum is less than or equal to some value x is F(x)ⁿ.

• Therefore, the probability the maximum is in (a, b] is F(b)ⁿ - F(a)ⁿ.

• This directly mirrors the discrete approach (k⁶ out of 6⁶ for dice) but with integrals or continuous CDFs.

• Pitfalls:

  1. Failing to adjust for the fact that continuous distributions have infinitely many possible values, so we can’t just “count.”

  2. Mixing up the PDF and CDF in computations for the maximum or misusing independence assumptions.

If an interviewer asks: "What if we are interested in the median or other order statistics (like the third highest) rather than the largest roll? How do we generalize from 'maximum' to 'k-th order statistic'?"

While we have formulas for the largest roll, order statistics in general are about the k-th largest (or k-th smallest) roll. The method:

• For discrete uniform dice, we can count the ways that exactly (k−1) dice exceed a certain value, a certain number of dice equal that value, and the rest are less. This gets complicated, but binomial coefficients and combinatorial arguments extend.

• A standard approach uses the “distribution of order statistics” in i.i.d. discrete random variables, where the probability mass function can be computed by enumerating how many samples are above, how many are equal, how many are below.

• Pitfall: The biggest challenge is complexity. The formula for a general order statistic has more terms, and it is easy to lose track of constraints like “no more than that many dice can exceed the stated value.”

If an interviewer asks: "How might rounding or measurement error affect the analysis if the 'die roll' can come from sensors or real-world measurements rather than perfect discrete outcomes of 1 through 6?"

In some physical or sensor-based scenarios:

• The measurement for each roll might be an approximate value, say a floating-point reading.

• We then typically define thresholds for deciding if the measured outcome is ‘close to 1,’ ‘close to 2,’ etc.

• The event “largest measured outcome is r” can get blurred if we have misclassifications or rounding: a true 5 might be recorded as 4.99 or 5.01.

• Pitfalls:

  1. Failing to account for the uncertainty in classification can lead to skewed probability estimates of the largest face.

  2. If the thresholds for rounding are not consistent, then the distribution of outcomes could systematically bias the reported largest roll.