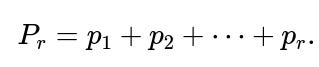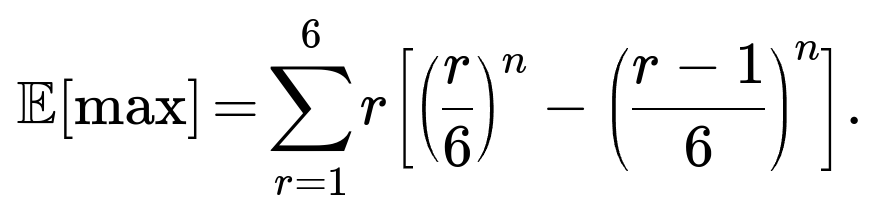ML Interview Q Series: Probability of Maximum Value in Dice Rolls Using Cumulative Distribution.
Browse all the Probability Interview Questions here.
A fair six-sided die is tossed n times. For each r in {1,2,3,4,5,6}, determine the probability that r is the highest value observed across all n throws.
Short Compact solution
Define an event where all n throws are at most r. This event has probability
because each throw has a 1/6 chance of producing any face, and we require each throw to show a value not exceeding r. Let the event that the maximum throw is exactly r be represented by subtracting the probability that all throws are at most (r−1) from the probability that all throws are at most r. Therefore, the probability that the largest number is r becomes
Comprehensive Explanation
When a fair, six-sided die is rolled n times, each outcome is one of the integers from 1 to 6, each with probability 1/6. We want the probability that the highest face value seen in all n trials is exactly r, where r goes from 1 up to 6.
The key idea is to frame this in terms of counting how many outcomes fail to exceed r, and how many fail to exceed r−1. By calculating the proportion of sequences that never exceed r and then subtracting those that never exceed r−1, we isolate the cases where the maximum is precisely r.
Considering Bᵣ as the event "all n rolls are at most r," the probability of Bᵣ is the fraction of all possible n-roll sequences in which each roll is no larger than r. Since each roll is independently at most r with probability r/6, it follows that
Similarly, Bᵣ₋₁ is the event "all n rolls are at most (r−1)," which happens with probability
Now define Aᵣ to be "the largest roll is exactly r." Observing that if the highest value is r, then none of the outcomes exceed r, and at least one outcome equals r. Equivalently, from a counting argument on entire sequences, this event can be separated out as all rolls at most r, minus all rolls at most (r−1). Hence the probability is
This is valid for r = 1, 2, 3, 4, 5, or 6. One can check that summing these probabilities from r = 1 to 6 yields 1, as it must, because the maximum must be some integer between 1 and 6.
The intuition can be understood in simpler terms: To get a maximum value of r, we count all ways that remain within r (no roll exceeding r). We then exclude all ways that remain within (r−1) to remove those sequences where the maximum is actually below r. That difference isolates the sequences where r is indeed the largest face observed.
Potential Follow-Up Question 1
How can we verify this probability formula by a simulation in Python?
It can be insightful to write a quick code snippet that simulates rolling a die multiple times and records the highest outcome. By comparing the frequency of each highest outcome to the theoretical probabilities, we can confirm the formula.
import random
from collections import Counter
def simulate_dice_rolls(num_simulations=10_000_00, n=5):
# We'll roll a fair six-sided die n times, repeat many simulations
# and see how often each r in 1..6 is the maximum observed.
results = []
for _ in range(num_simulations):
rolls = [random.randint(1, 6) for __ in range(n)]
results.append(max(rolls))
# Count occurrences of each possible maximum
count = Counter(results)
# Compute empirical probability
for r in range(1, 7):
empirical_prob = count[r] / num_simulations
theoretical_prob = (r/6)**n - ((r-1)/6)**n if r > 1 else (1/6)**n
print(f"r = {r}: Empirical = {empirical_prob:.5f}, Theoretical = {theoretical_prob:.5f}")
simulate_dice_rolls()
This code approximates the probabilities experimentally and then prints them alongside the theoretical values. For sufficiently large num_simulations, the empirical results should align closely with the derived probabilities.
Potential Follow-Up Question 2
What happens in edge cases, like r = 1 or r = 6?
For r = 1, the event that the largest number is 1 means every throw resulted in a face of 1. The probability for that is
Our formula also confirms this. When r=1, there is no term for (r−1), so it simply becomes (1/6)ⁿ.
For r = 6, the event that the largest value is 6 is the complement of the event that the largest value is at most 5. Thus the probability can be found by 1 − (5/6)ⁿ. Our expression also matches because
Potential Follow-Up Question 3
If n is large, what interesting behavior emerges?
As n grows, the chance that the maximum roll is 6 grows significantly. In fact, the probability that the highest number is less than 6 shrinks quickly. More precisely, the probability that the maximum is 6 after n rolls is
which approaches 1 as n → ∞. This illustrates that with many rolls, it becomes very likely that at least one roll will be a 6.
Potential Follow-Up Question 4
How might this concept be extended to different dice or distributions?
The same reasoning can be applied to any discrete distribution where you want to find the probability that the maximum among n samples is a particular value. If you had a d-sided die, the probability that the maximum is r would be
for r in {1,...,d}. If you consider continuous distributions (such as rolling a random variable that is uniformly distributed from 0 to 1), the principle remains the same, but you would integrate instead of summing, and compute the cumulative distribution function (CDF) to find the probability of all values being at most r, then take differences accordingly.
Potential Follow-Up Question 5
How do we ensure that these probabilities sum up to 1 over r = 1..6?
In discrete scenarios, partitioning events where the “maximum is r” for r=1..6 forms a disjoint set covering all possible outcomes. Because each n-roll sequence has a unique maximum, the probabilities over r=1..6 must add up to 1. One can quickly verify that summing
over r = 1..6 yields 1. This is a simple telescoping sum in which intermediate terms cancel, leaving the final expression equal to 1.
All these details underline a general principle: to find the probability that a maximum among multiple samples lies exactly at a certain value, calculate the probability that all samples do not exceed that value, then subtract the probability that they are strictly less than that value. This approach elegantly handles discrete distributions such as dice rolls.
Below are additional follow-up questions
What if the die is biased so that each face does not have equal probability?
In a scenario where each face of the die has a different probability (for instance, a loaded die), the probability that a single roll is at most r becomes the sum of the probabilities of the faces 1 through r. Denote these probabilities by p₁, p₂, …, p₆, where p₁ + p₂ + … + p₆ = 1. Let
Then, the probability that all n rolls are at most r is
and the probability that the largest number observed is exactly r becomes
A subtlety arises if some faces have zero probability. If pᵣ = 0 for certain r, then the highest face might have no chance of being that particular value. You would need to verify that each face’s probability is strictly between 0 and 1 if you are relying on the possibility of every face being observed. Another pitfall is numerical stability: if probabilities are extremely small or large, you can face underflow or overflow issues in code, requiring special handling such as log-transforms.
How to find the probability that exactly k dice show the maximum value r?
To tackle the event “exactly k out of n dice show the face r, and r is the largest observed,” we can break this down into two components:
Ensure that none of the other (n − k) dice exceed r, which means they are at most (r − 1).
Precisely k dice match r, and the remaining (n − k) are strictly less than r.
We can use a binomial coefficient to count how many ways to choose the k dice that show r. Specifically, for a fair die:
Probability that a single die equals r is 1/6.
Probability that a single die is at most (r − 1) is (r − 1)/6.
Probability that a single die is at most r but strictly less than r is (r − 1)/6.
Hence for exactly k copies of r:
One must confirm that among the (n−k) dice, none exceed r, which is accounted for by having them ≤ (r−1). Numerical pitfalls include mixing up “at most r” vs. “exactly r” in the count. Also, if r=1, then k must be either 0 or n (and if it’s 0, that violates having a maximum of 1). This boundary condition needs careful checking so you do not end up with a contradictory scenario.
Can we extend this to compute the expected value of the maximum roll?
Yes, the expected maximum can be computed by summing over r × P(Aᵣ) for r from 1 to 6, where P(Aᵣ) is the probability that the maximum is r. For a fair die,
A common pitfall is to try to compute the expected maximum by averaging the maximum from each outcome. It’s simpler to use the closed-form approach above. One subtlety with large n is that the result heavily weights the higher faces—indeed, as n grows, the maximum skews strongly toward 6.
How does dependence between rolls affect the probability distribution of the maximum?
The derivation we use for the maximum assumes independence between different rolls: each roll does not affect the others. If the rolls are correlated (for example, from a physical process or in a scenario where rolling one face influences the next outcome somehow), then the probability factorizes differently. You can’t just raise (r/6) to the nth power anymore to find the probability that all outcomes are at most r.
In a real-world scenario, dice might be slightly imperfect or external factors might create correlations (like rolling on a surface that causes the die to show certain values more often under certain conditions). Handling this requires modeling the joint distribution of the outcomes rather than the product of marginals. This dramatically increases complexity, and you’d usually need empirical or measured correlation coefficients to handle it accurately.
What if the dice outcomes are only partially observed?
Sometimes in practical data-gathering situations, you might not see every roll. If some of the rolls are hidden or lost, you only know the outcomes for a subset. You might still want to estimate the distribution of the maximum of all n rolls. In such a case, you might use missing-data strategies:
If the missing data are assumed to be missing completely at random, you can attempt an unbiased estimate of the maximum using partial observations plus likelihood-based reasoning for what the unobserved rolls might have been.
If the missing data are not random (perhaps you only lose data when high rolls occur), your analysis will be biased unless you correct for that mechanism.
A serious pitfall is incorrectly assuming missing data is random, leading to an underestimate or overestimate of the probability that the maximum hits a large value. In real-world analytics or ML pipeline logs, missing data is rarely purely random.
Is there a continuous analog of this result?
Yes. Suppose you have n i.i.d. samples from a continuous distribution with cumulative distribution function (CDF) F(x). The probability that the maximum is at most a certain value x is [F(x)]ⁿ. If you want the probability that the maximum lies within some small interval (x, x+dx), you differentiate the above. Specifically, the probability that the maximum is in (x, x+dx) is n [F(x)]^(n−1) f(x) dx, where f(x) is the probability density function (PDF). A pitfall here is assuming a discrete approach applies directly to continuous data or vice versa without adjusting for integrals versus sums. Another subtlety is if the distribution is unbounded; care must be taken in integrals that extend to infinity or negative infinity.
How might we apply this concept in a ranking or ordering system?
When multiple items are randomly assigned scores (like recommendation systems or ranking candidates by some feature), the top score among n items can be seen as a “maximum roll.” You can extend the same logic:
Identify the probability that an item’s score is less than or equal to some threshold.
Raise that to the nth power to find the probability all items are below or equal to that threshold.
Subtract from the scenario with a smaller threshold to get the chance that the maximum is within a narrow band.
A subtlety arises if items are not identically distributed—some items might systematically have higher or lower expected scores. Another pitfall is ignoring tie scenarios (the exact “highest” might be shared by multiple items). This often matters in real-world ranking, where many items might end up with the same top score.
How do we handle real-time dashboards that continuously display the highest observed roll?
If you are receiving dice rolls in a streaming fashion, you might want the probability that the maximum so far is r at any point in time. At each new roll:
Update the maximum if the newly observed value exceeds the current maximum.
Track the distribution of possible maxima as you accumulate more rolls.
A pitfall is that simple formulas like (r/6)ⁿ rely on the entire set of n rolls being in memory. In streaming contexts, you typically only store the current maximum (and perhaps some additional statistics). Another subtlety is ensuring the distribution is updated properly across many increments without reprocessing the entire history each time. In a machine learning system with high throughput, you might store summary statistics (like how many times each face has been observed) to maintain an approximate distribution of the maximum without incurring high memory or computational costs.