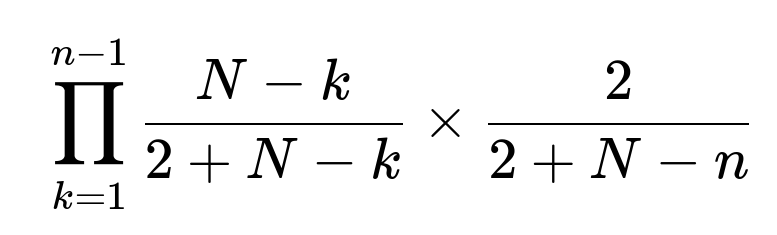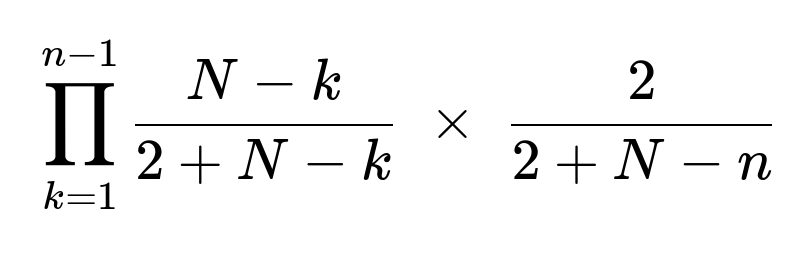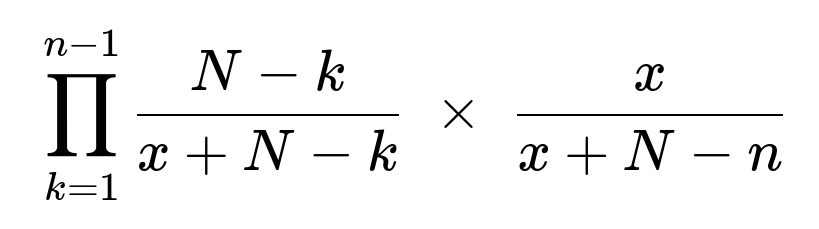ML Interview Q Series: Probability of n-th Placement in Lottery with Advantage via Conditional Probability.

Browse all the Probability Interview Questions here.

You are among N players that will play a competition. A lottery is used to determine the placement of each player. You have an advantage. Two tickets with your name are put in a hat, while for each of the other players only one ticket with her/his name is put in the hat. The hat is well shaken and tickets are drawn one by one from the hat. The order of names appearing determines the placement of each player. What is the probability that you will get assigned the n-th placement for n = 1, 2, …, N?

Short Compact solution

Define A_n to be the event that your name appears in the n-th draw and A_i the event that your name does not appear in the i-th draw for i=1,…,n−1. We use the multiplicative law:

P(A₁ A₂ … A_n) = P(A₁) × P(A₂ | A₁) × … × P(A_n | A₁A₂…A_n−1).

Hence, the probability that you get the n-th placement is

Comprehensive Explanation

Setup and Basic Idea

We have N total players. You have 2 tickets in the hat, while each of the other N−1 players has exactly 1 ticket each. Therefore, the total number of tickets is (N−1) + 2 = N+1. When tickets are drawn one by one:

• The 1st ticket drawn corresponds to the 1st placement (winner of the 1st place).

• The 2nd ticket drawn corresponds to the 2nd placement, and so on.

• The n-th ticket drawn corresponds to the n-th placement.

We want the probability Pn that your name is exactly in position n in this drawn sequence.

Probability Computation via Conditional Probability

We define:

• A_n: event “Your ticket is drawn in the n-th draw.”

• A_i: event “Your ticket is not drawn in the i-th draw,” for i=1,…,n−1.

We need P(A₁A₂…A_n), which unfolds by the chain rule for probabilities:

P(A₁A₂…A_n) = P(A₁) × P(A₂ | A₁) × … × P(A_n | A₁A₂…A_n−1).

Step 1: Probability of not being drawn on the 1st draw

• There are 2 tickets with your name and N−1 tickets corresponding to other players, for a total of N+1 tickets.

• The probability that you are drawn on the 1st draw is 2/(N+1).

• So the probability you are not drawn on the 1st draw is (N+1−2)/(N+1) = (N−1)/(N+1).

Hence, P(A₁) = (N−1)/(N+1).

Step 2: Probability of not being drawn on the 2nd draw (given not drawn on the 1st)

• If your ticket is not drawn on the 1st draw, that means one of the other N−1 players’ tickets was drawn. Now the total tickets left is N (because one non-your ticket was removed).

• Out of those N remaining tickets, 2 are still yours.

• The probability you are not drawn on the 2nd draw is (N−2)/N.

Hence, P(A₂ | A₁) = (N−2)/N.

Continuing in General

At the k-th draw (for k ≤ n−1), if your ticket has not been drawn so far, exactly k−1 tickets have been removed, all belonging to other players. The total tickets left is (N+1) − (k−1) = N+2−k, and your 2 tickets are still in the pool. Thus:

• Probability you are not drawn at the k-th draw (given not drawn in all previous draws) is (N+2−k−2)/(N+2−k) = (N−k)/(N+2−k).

So for k=1,…,n−1, the factor for “not drawn at the k-th step” is (N−k)/(N+2−k).

Probability of being drawn exactly at the n-th draw

Finally, once you survive the first n−1 draws, the probability of being the n-th draw is:

2 / [ (N+1) − (n−1) ] = 2/(N+2−n).

Hence multiplying them all together:

P(A_n exactly) = ∏_{k=1 to n−1} [ (N−k)/(N+2−k ) ] × [ 2/(N+2−n) ].

This simplifies to:

where

• N is the total number of players,

• n is the position of interest,

• 2 is the number of tickets in the hat with your name.

Intuitive Interpretation

Since you have one extra ticket compared to every other player, your chance of appearing in each draw is slightly larger at every step. This formula quantifies precisely how that advantage spreads over all possible positions from 1 to N. Notice that for n=1, the probability is 2/(N+1). For large n, you first must fail to show up in earlier draws, and then succeed exactly on the n-th draw.

Example and Numerical Check

Suppose N=3 (4 total tickets: 2 are yours, and 1 each for two other players). The placements are among players A (you) and B, C (others). We want P(you are 1st), P(you are 2nd), P(you are 3rd).

• P(you are 1st) = 2/4 = 1/2.

• P(you are 2nd):

  • Not 1st: 2 tickets of others out of 4 total → Probability(not 1st) = (4−2)/4 = 2/4 = 1/2.

  • Then be 2nd: Now 3 tickets left, 2 are yours → Probability(be 2nd) = 2/3.

  • Multiply → 1/2 × 2/3 = 1/3.

• P(you are 3rd):

  • Probability(not 1st) × Probability(not 2nd) × Probability(be 3rd in the last step).

  • We can also confirm P(you are 3rd) = 1 - P(you are 1st) - P(you are 2nd) = 1 - 1/2 - 1/3 = 1/6.

This small example aligns with the general formula.

Follow-up question: How do we generalize if you had x tickets instead of 2?

If you had x tickets instead of 2, while each of the other N−1 players still has exactly 1 ticket, then:

• The total number of tickets in the hat is x + (N−1).

• The probability you are not drawn on the k-th draw, given you were not drawn in the first k−1 draws, becomes:

(N+1−x−k) / (N+1−k),

because initially there are x tickets with your name, and after k−1 draws (all from the other N−1 players), there are x tickets of yours left out of N+1−(k−1) = N+2−k total. More precisely, the factor “(N+1−x−k)/(N+2−k)” might need to be re-evaluated carefully if we reduce x > 1 in subsequent draws, but the logic is that as long as your name has not been drawn at all, you retain all x tickets. Hence the final formula for the probability of being drawn exactly at the n-th draw would be:

where x is the number of your tickets.

Follow-up question: How does this probability behave for large N?

For very large N (with only 2 of your tickets), your probability to appear in early draws is roughly 2/(N+1). Because N is large, the difference between having 2 tickets and having 1 is less dramatic. Effectively, the distribution of your position flattens out, but it remains slightly more likely to see your name earlier than other single-ticket players if all tickets are drawn. If N is extremely large, the difference between 2 tickets vs. 1 ticket might be small enough that your probability across all positions becomes nearly uniform at 1/N, but with a slight bias toward earlier placements.

Follow-up question: What is the expected placement (position) you receive?

You can calculate the expected position by summing n×Pn for n=1 to N, where Pn is the probability your name appears in the n-th draw. While the closed-form expression for the sum can be derived, a simpler conceptual approach is:

• The expected position is the average draw index at which your ticket is pulled out. Since each draw is equally likely to be any ticket (with a weighting by the number of tickets you have left each time), you effectively have 2 tickets out of N+1. By symmetry arguments (or by summing n×Pn), the expected position can be found to be (N+1)/(2+1) = (N+1)/3 if you want a quick argument from known results about random permutations with weighting.

• More rigorously, E[position] = Σ_n=1^N n × Pn. You can either do that sum directly (some references do) or rely on a known combinatorial identity.

Follow-up question: Could we simulate this to verify in Python?

Yes. Below is a quick Python snippet that performs a Monte Carlo simulation for large repeats to estimate Pn:

import random
import numpy as np

def simulate_probability(N=5, num_sim=10_000_00):
    # We label the 'tickets': your tickets as 'Y' x 2, others as O1, O2, ... O(N-1)
    # But for simulation, we just store them in a list: 'Y','Y','O','O','...'
    tickets = ['Y']*2 + ['O']*(N-1)
    placement_counts = [0]*N  # placement_counts[i] will count how often we get i-th position (i from 0 to N-1)

    for _ in range(num_sim):
        random.shuffle(tickets)
        # The order of the shuffled list is the drawn order
        # Find where the first 'Y' occurs
        your_position = tickets.index('Y')  # 0-based index
        placement_counts[your_position] += 1

    # Convert to probabilities
    probabilities = [count/num_sim for count in placement_counts]
    return probabilities

if __name__ == "__main__":
    N = 5
    probs = simulate_probability(N=N, num_sim=1_000_00)
    print("Estimated probabilities for N=5:")
    for i, p in enumerate(probs, start=1):
        print(f"Position {i}: {p:.5f}")

This code:

1. Constructs a list of N+1 tickets, including 2 labeled 'Y' for you, and N−1 labeled 'O' for others.

2. Shuffles the tickets repeatedly.

3. Identifies the index of the first occurrence of 'Y' in the shuffled list (because that is your earliest appearance).

4. Tally the result and estimate probabilities.

Comparing these estimated probabilities to the theoretical values from the formula should confirm correctness.

Follow-up question: What if the competition stops drawing after awarding the top K places?

If the competition only draws K places out of the N players (K < N), then the question might be: “What is the probability you appear in the top K positions?” or specifically “What is the probability you get i-th place for i=1…K?” The derivation is very similar, but we only consider the first K draws. The total probability that you are among the top K is the sum of probabilities that your name shows up in any of those K draws:

P(position in {1,...,K}) = Σ_n=1^K Pn.

Once again, each term Pn can be computed by skipping the first n−1 draws and then landing exactly on draw n, up to K.

All these variations follow the same combinatorial/conditional probability logic. The main difference is that once the competition stops, if you are not drawn in the first K, you have zero chance of any placement beyond K.

Below are additional follow-up questions

What if there is a sudden rule change mid-draw allowing a random number of extra tickets for another player?

Imagine partway through the lottery process (say, after a few tickets have already been drawn), an organizer decides that one of the other players also deserves an advantage and adds some extra tickets for that player into the pool before the next draw. How would this shift your probability of getting a certain placement?

Detailed Answer

• Step-by-step logic: Initially, your probability distribution follows the well-known logic that you have 2 tickets, while the others have 1 each. But after k draws, if new tickets for another player are added, the total count of tickets and their composition changes.

• Before the change: For the first k draws, you can compute the probability of not being drawn for each of those draws using the original ratio (for each draw, you have 2 tickets vs. the other total).

• At the moment of rule change: Suppose you are still in the hat (i.e., none of your tickets has been drawn yet). Now an extra m tickets for a particular other player are tossed into the hat. Suddenly the hat composition includes:

  • 2 of your tickets (if you haven’t been drawn)

  • 1 ticket for each of the remaining players (if they haven’t been drawn)

  • m additional tickets for the favored player

• Post-change draws: The probabilities must be recalculated from that point onward, taking into account the new total number of tickets. This changes your probability in two major ways:

  1. You survived the first k draws.

  2. Your odds of being drawn on the next step are 2 / (current total), but that total is now bigger than anticipated due to the extra m tickets.

• Potential pitfalls:

  • If the add-on occurs after some tickets are removed, you must carefully track whether your tickets or that other player’s original ticket(s) are still in the hat. If the other player’s single original ticket was removed, yet they add m new ones, that player effectively re-enters the lottery with a changed chance.

  • If the new tickets are supposed to represent a “fair” compensation, you may need to consider the exact number m that ensures the final distribution of positions is still acceptable to all participants.

• Real-world scenarios: In real contests or raffles, new rules might be introduced to offset perceived unfairness. Such rule changes can substantially alter the probabilities after partial information (like who was drawn in the first few picks) is already revealed.

How do dependencies among different positions matter if the contest awards multiple “special” prizes at random draws?

Sometimes there might be separate special prizes associated with specific random draws (for example, the 2nd draw gives a “bonus trophy,” the 5th draw gives “free merchandise,” and so on). How does the probability you get a later special prize depend on the chance you might have already won an earlier one (assuming you can’t win more than once)?

Detailed Answer

• Multiple dependent events: In standard scenarios, being drawn for an early position removes you from the hat entirely for the subsequent draws. This means you either appear exactly once (at the earliest draw in which one of your tickets gets picked) or not at all, so you can’t win multiple prizes.

• Incompatibility or exclusivity: If any special prize is associated with draw number i, only the person drawn at step i gets that prize. Since you cannot appear in both step i and step j if i < j, the events “You get the special prize at step i” and “You get the special prize at step j” are mutually exclusive for i ≠ j.

• Conditional probability perspective: If you want to know the probability that you specifically get the special prize on the j-th draw (and not on the earlier i-th draw for i<j), you can factor in the must-fail for earlier positions and must-succeed exactly on j. This is effectively the same logic used for the probability of being the j-th placement, but specifically interpreted for the j-th prize.

• Potential pitfalls:

  • If your name can appear more than once (e.g., your multiple tickets are returned to the hat after a draw), the scenario changes drastically: you could theoretically win multiple prizes. That is a different mechanical process than the usual no-replacement draw.

  • If partial knowledge is revealed (like you see who won at earlier draws), your conditional probabilities must be updated after each draw.

• Real-world issues: Fundraisers and raffles often have multiple “door prizes” announced at different times. The independence or lack thereof between draws can cause confusion for participants. If a participant can win multiple times, that must be stated clearly; otherwise, removing their ticket after the first win ensures exclusivity.

What if there is uncertainty in the total number of players (or tickets) at the time of the draw?

Sometimes the exact count of participants might be unknown—maybe some are absent, or some join last minute, or the hat is missing a ticket. How does the probability distribution change if we do not know N for certain?

Detailed Answer

• Unknown N: You might only have a probability distribution over possible values of N. For instance, you think there’s an 80% chance that N=10 but a 20% chance it’s actually 11. Then your final probability of being drawn in the n-th position is an expectation across these scenarios: (80% × Probability given N=10) + (20% × Probability given N=11).

• State of knowledge: This is a Bayesian approach where your prior distribution over N (the possible number of players) must be taken into account. If you observe partial draws or see how many unique names appear early on, you can update your posterior for N.

• Pitfalls:

  • If an entirely new player arrives mid-process, that changes the total from N to N+1. Now you must handle the draws that have already occurred plus the updated future draws with the extra tickets.

  • If some tickets were lost or miscounted (like the hat actually has only 1 of your tickets instead of 2), your theoretical assumption about having 2 tickets might be wrong from the start.

• Real-world scenario: Conferences or tournaments that allow last-minute registrations might finalize brackets only after some participants check in. If you came early with your extra advantage, but then more participants arrive, your advantage ratio might shrink or the total distribution changes.

How do we handle the case where multiple people (besides you) also have multiple tickets?

In the original scenario, you have 2 tickets, and every other participant has 1. What if there are several “privileged” players, each with multiple tickets, and others still have just 1 each?

Detailed Answer

• Generalization: Suppose:

  • You have x tickets.

  • M other players each have y_i tickets (some might have 2, some 3, etc.).

  • The remaining players each have 1 ticket.

• Computing your position probability: The logic is the same, but the total ticket pool is now x + Σ(y_i) + (number of single-ticket players). At each draw, the chance of not picking you depends on how many tickets remain for you relative to how many remain overall.

• Step-by-step:

  1. At draw k=1, Probability(not you) = 1 − x/(total tickets).

  2. At draw k=2, if you still haven’t been drawn, that implies some other player’s tickets were removed. But how many tickets for each other privileged player remain depends on whether that draw belonged to a single-ticket player or to a privileged player. So you need a conditional structure that branches out for each possible draw outcome.

  3. For a simpler formula, it suffices to note that if none of your x tickets have appeared by draw k−1, you still have x tickets in the hat. The total left is total tickets − (k−1). So Probability(not you at step k given not you so far) = (total tickets − (k−1) − x) / (total tickets − (k−1)).

  4. Finally, Probability(you at step n given not you in previous n−1 draws) = x / (total tickets − (n−1)).

• Pitfalls:

  • The presence of other multi-ticket holders changes the distribution each time they or you get drawn. If they appear earlier, they exit with all their tickets, eliminating a large chunk of total tickets at once.

  • In the strict no-replacement model, once a multi-ticket holder is drawn, all that holder’s tickets effectively become irrelevant for future draws.

• Real-world example: In large raffles, sponsors or VIPs might get multiple entries, while some other special guests also get multiple, leading to a complicated but systematically derivable probability distribution.

How do we confirm that all n from 1 to N indeed sum to 1 for your probabilities?

It might seem obvious that your probability of being 1st, 2nd, …, or Nth should sum to 1, but can we show this explicitly (and what if it doesn’t sum to 1)?

Detailed Answer

• Summation property: In standard no-replacement draws, exactly one of your tickets must appear at some unique position from 1 to N (assuming no two tickets with your name can both count for different positions). Hence the sum of probabilities P(position = n) for n=1,...,N must equal 1.

• Sketch of proof:

  1. Let X be the random variable denoting the earliest draw index where your name appears.

  2. X must take a value in {1, 2, …, N} or possibly “not drawn at all” if you had fewer tickets than N? Actually, with 2 tickets, you are guaranteed to appear at some position since the total number of distinct positions is N, and you are among the N players. (In some permutations, you might worry about “not drawn,” but actually in a scenario of N players, your name must appear in the top N draws because the number of distinct tickets that can appear in the top N draws is exactly N, and you have 2 tickets among N+1 total. However, it’s possible one ticket remains undrawn if N < N+1, but that leftover is still your second ticket if the first one was drawn. Hence your earliest appearance is definitely among the first N draws.)

  3. Because the draws form a partition over all possible permutations of tickets, the probability of each distinct scenario is well-defined. Summing over all positions must yield 1.

• Pitfalls:

  • If you are worried about the possibility that neither of your tickets is drawn because there is a leftover ticket in a bigger pool, recall that the competition draws exactly N distinct tickets to assign N placements. With N total players, each player (including you) must appear exactly once, so you do get drawn somewhere.

  • If the logic says your sum is not 1, that indicates a miscount or missing event in your derivation.

• Real-world check: This is essentially verifying that the outcome “you appear in position 1 or 2 or … or N” covers every possibility, which it does if the drawing is used to assign each distinct placement exactly once to each of the N players.

How is the distribution changed if each ticket you have corresponds to a different skill level or separate entry, and you can occupy multiple placements?

Sometimes the rules might allow you, in principle, to hold more than one “spot” if each of your tickets represents a distinct “team” or “instance.” In that scenario, you could appear in multiple draws. How does that alter the probability that the first time you appear is at the n-th draw, or that you appear in multiple positions?

Detailed Answer

• Multiple wins for the same person: In a typical scenario, if you get drawn at one position, all your tickets are effectively considered “used up” for that event. But if the rules state that each ticket you own is a separate entity that can earn a separate spot, then you do not remove your remaining tickets from the lottery after your first draw.

• Probability changes:

  1. For the earliest time your name appears, you still have a chance to appear in subsequent draws as well.

  2. The event “You appear in the n-th draw for the first time” only means your first ticket was not drawn in draws 1,...,n−1, but you could have other tickets still in.

  3. The standard formula for the earliest appearance might remain identical. But your probability of also appearing at draw n+1 or n+2, etc., can only be computed by tracking how many of your tickets remain after each appearance.

• Pitfalls:

  • If the rules allow multiple placements for one person, the total number of unique “positions” among N places is not well-defined for “players.” Possibly the same person occupies multiple top spots, which might be unusual for a real competition.

  • In more realistic terms, multiple entries often represent different teams or categories. So be sure to interpret the meaning of “placement” correctly.

• Real-world scenario: It can happen in tournaments where a single sponsor can register multiple participants. If those participants are effectively the same person or brand, you might see multiple placements going to that same sponsor’s entries. Probability calculations must reflect that each entry remains in the competition unless specifically removed or merged.

How do we handle extremely large or small edge cases (e.g., N=1, N=2, or extremely large N)?

• N=1: If there is only 1 player (you), then you trivially occupy the 1st position with probability 1. The formula for the probability that you appear in the n-th position for n>1 is moot because only one position exists. This is a trivial boundary case but reveals that we must handle degenerate scenarios carefully.

• N=2: You have 2 tickets, the other player has 1 ticket, so total 3 tickets. Then the probability that you get 1st place is 2/3. The probability you get 2nd place is computed by not being drawn first (1/3) and then drawn second (2/2). So that’s 1/3, and it sums to 1. That’s consistent with the general formula.

• Extremely large N:

  • As N grows, the probability that you appear in the earliest positions changes in a small but non-negligible way compared to a single-ticket holder. Numerically, you can see that for n=1, it’s 2/(N+1). This approaches 0 as N→∞, but is still twice as large as if you had only 1 ticket (which would be 1/(N+1)).

  • Summing or analyzing the distribution might require approximate methods if you want explicit closed forms. However, the limiting distribution often flattens out, with only a minor edge in the early draws.

• Pitfalls:

  • For very large N, floating-point precision in simulations or combinatorial calculations can become an issue.

  • For extremely small N, you might need to handle cases like N=1 or N=2 as special logic in code or analysis.

• Real-world scenario: If you are applying this to large-scale raffles or tournaments with thousands of participants, you might rely on simulation or limiting approximations. In smaller tournaments, you can rely on direct combinatorial computations.