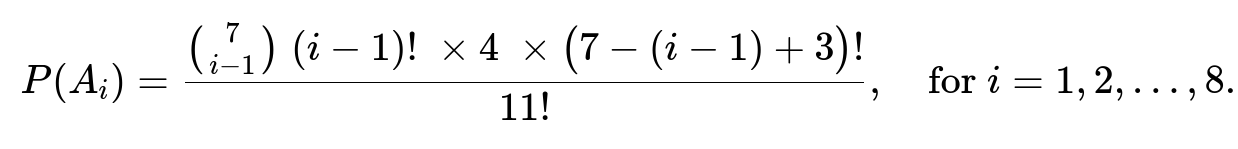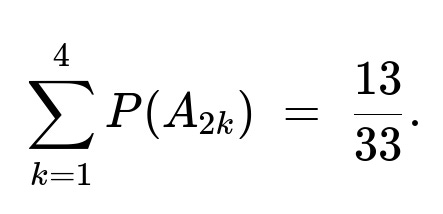ML Interview Q Series: Probability Without Replacement: Odds Second Player Draws the First Red Ball
Browse all the Probability Interview Questions here.
Bill and Mark take turns picking a ball at random from a bag containing 4 red balls and 7 white balls, without replacement. Mark picks first. What is the probability that Bill is the first person to pick a red ball?
Short Compact solution
One way to solve this is to label the 11 balls distinctly and consider all permutations of these 11 balls (4 red and 7 white). Define Ai to be the event that the first red ball appears exactly on the i-th draw. By counting how many permutations satisfy this condition, one obtains
Because Bill picks on the even-numbered draws (2nd, 4th, 6th, and 8th), the probability that Bill is the first to get a red ball is
Hence, the probability that Bill is the first to pick a red ball is 13/33.
Comprehensive Explanation
This problem involves two players, Mark and Bill, drawing from a bag of 11 total balls without replacement. There are 4 red and 7 white balls. Mark draws first (on the 1st, 3rd, 5th, 7th draws, etc.), and Bill draws second (on the 2nd, 4th, 6th, 8th draws, etc.). We want the probability that Bill is the first to pick a red ball.
A direct combinatorial approach is to note that if the first red ball appears at the i-th draw, then:
There must be exactly i-1 white balls in the first i-1 positions.
The i-th ball is red.
The remaining positions can be any arrangement of the leftover balls.
By enumerating permutations and dividing by the total 11! permutations, one arrives at the expression for P(Ai).
Because Bill only draws on the even-numbered turns 2, 4, 6, and 8, we sum up the probabilities of the event “the first red ball appears at an even draw”:
The first time a red ball appears at draw 2 means the 1st ball was white, and the 2nd ball is red.
Similarly for draw 4, it means the first 3 draws were white, the 4th is red, etc.
This is continued up to draw 8. (We do not need to go beyond draw 8 for the first red ball because there are 4 red balls in total, and if the first 7 draws are all white, the 8th draw must be red.)
Summing these probabilities gives 13/33.
From a more intuitive viewpoint, Bill’s advantage or disadvantage depends on whether Mark happens to draw a red ball before Bill. One might attempt a purely probabilistic argument by listing Mark’s and Bill’s draw positions and computing conditional probabilities of no red ball in the preceding draws. However, the combinatorial approach directly handles all cases simultaneously, leading to the 13/33 result.
Potential Follow-up Questions
How could we verify this result by simulation?
One might write a Python simulation that performs many trials of this turn-based drawing process, counts how often Bill picks the first red ball, and then estimates the probability. Each trial would randomly shuffle an array of 4 red and 7 white, track who picks at which index, and check who encounters the first red ball.
A simple outline in Python might be:
import random
def simulate_bill_probability(num_sim=10_000_00):
import math
successes = 0
for _ in range(num_sim):
balls = ['R']*4 + ['W']*7
random.shuffle(balls)
# Mark picks on indices 0, 2, 4, 6,...
# Bill picks on indices 1, 3, 5, 7,...
first_red_picker = None
for i, ball in enumerate(balls):
if ball == 'R':
first_red_picker = 'Mark' if i % 2 == 0 else 'Bill'
break
if first_red_picker == 'Bill':
successes += 1
return successes / num_sim
print(simulate_bill_probability())
Over many runs, this will converge toward 13/33 ≈ 0.3939.
Why does the first red ball never appear after the 8th draw?
Because there are 4 red balls among 11 total. If the first red had not appeared by the time we have drawn 7 balls, that means all 7 drawn were white. In that scenario, the remaining 4 balls are all red. Hence the next draw (which is the 8th draw) is guaranteed to be red, so the very first red ball must occur by the 8th draw at the latest.
How would the probability change if the players replace the balls after each draw?
With replacement, each draw is an independent event with probability 4/11 of being red on any draw. If Mark always draws first each round, the probability that Bill draws the first red is different because the draws do not eliminate balls. You would have to compute the probability that Mark does not get a red on his first draw but Bill does on his first draw, or if neither gets red in the first round, we continue to the second round, and so on. This becomes a geometric-like series calculation, but it no longer matches the 13/33 solution because the draws are independent with replacement.
What if Bill picks first instead?
If Bill were the one to draw first, the roles would be reversed, and we would calculate the probability that Bill draws the first red in that scenario. By symmetry, if Bill picks first from 4 red and 7 white, the probability changes because Bill now has the first opportunity. You can set up a similar combinatorial approach or run a simulation. In fact, if Bill picks first, the probability that Bill is the first to draw a red would be larger than 13/33 since Bill holds the advantage of going first.
If there were more than two players taking turns, how would we generalize?
You could define events for the first red ball to occur on each of the possible draw positions and then determine which player draws at that position. You would sum the probabilities of the events that correspond to a specific player’s turn. The combinatorial logic becomes more involved, but the principle remains the same: count all permutations that yield a first red on a certain draw, check which player is drawing on that draw, and then divide by the total permutations.
Are there any combinatorial pitfalls in problems like these?
A common pitfall is forgetting that the players draw in a strict sequence, so the position (turn order) matters. Another pitfall is failing to account for the fact that no red appears in previous draws, leading to missing or double-counting certain permutations. Another subtlety is ensuring you realize the maximum possible position for the first red ball if there are multiple red balls in the bag.
These are the main ways to think about and verify the probability that Bill is the first person to pick a red ball in this turn-based drawing scenario without replacement.
Below are additional follow-up questions
Could we solve this using a negative hypergeometric distribution perspective, and why might that be simpler?
One elegant way to tackle the question "What is the probability that the k-th draw is the first red ball?" is through the negative hypergeometric distribution. The negative hypergeometric distribution directly models the scenario of drawing from a finite population without replacement until a certain number of "successes" (red balls) appears.
When dealing with "Who draws the first red ball?" we can map it directly to this distribution by focusing on the trial at which the first success (red ball) is observed. Each position in the sequence of draws (from 1 through 11) is equally likely if we consider all permutations. The negative hypergeometric formula tells us the probability that exactly i-1 "failures" (white balls) occur before the 1st "success" (red ball).
In practice, this approach sidesteps the need to count permutations directly since the distribution inherently takes care of the combinatorial relationships for you. A pitfall can be mixing up the negative hypergeometric distribution with the hypergeometric distribution, as the latter describes how many successes you get in a fixed number of draws, rather than when the first success appears.
Could the result differ if we do not thoroughly randomize the balls in the bag?
In standard probability treatments like this, we usually assume that each arrangement of the balls in the bag is equally likely. This is equivalent to assuming the balls are fully randomized and that every draw is equally likely to be any of the remaining balls.
If the randomization process is not thorough—for instance, if there is some bias in how the balls are mixed—the probability of drawing a red ball at certain positions can change. A real-world example might be if someone just placed four red balls on top of the white ones without any proper shuffling, thus giving an increased chance that Mark (who draws first) would pick a red ball early. In that scenario, the 13/33 result would not hold.
A subtle real-world issue: Even if you physically shuffle the bag, there might still be slight biases in how the balls settle. In practice, if you suspect incomplete shuffling, you might run multiple draws or deliberately swirl the bag to ensure uniform mixing.
What if Bill and Mark do not reveal whether the drawn ball is red or white?
If neither player reveals what they drew, the game becomes more of a hidden-information scenario. The question "Who picked the first red ball?" might remain uncertain until the end, or players might attempt to infer what the other person drew based on partial knowledge of the number of red/white balls.
However, from a purely mathematical standpoint—if you were to retroactively check who must have encountered the first red ball—the probability distribution remains the same under the assumption that the initial arrangement is uniformly random. Each position for the first red ball in the sequence is still equally likely across all permutations. The main difference is that the players themselves do not know in real-time who got the first red ball unless they reveal it.
Potential pitfall: Some might incorrectly assume that secrecy changes the probability. In reality, if all permutations are still equally likely, the secrecy only affects the players’ knowledge states, not the underlying combinatorial probabilities.
How does the approach change if Bill and Mark each draw multiple balls per turn?
Sometimes variations of such problems allow each player to draw a certain number of balls each turn. For instance, if Bill and Mark each draw two balls on their turns instead of one, we’d have to update the condition for "the first red ball appears in a given turn." Specifically, each "turn" would now involve two balls drawn consecutively by the same person. Then we must check whether the first red ball came on the first or second ball of that turn, and so on.
The event that Bill is the first to draw a red ball can happen if:
Mark draws 0 red balls in his entire turn,
Then Bill draws at least 1 red ball in his subsequent turn,
And that ball is earlier than any red ball Mark may have drawn on a later turn.
The counting can get more involved because in one turn, a player might draw more than one red ball. The main pitfall here is to avoid oversimplifying "turns" as single-draw events when each turn has multiple draws.
How would the solution change if we only have partial information on how many red and white balls there are?
Imagine a scenario where you know there are a total of 11 balls, but you do not know if it’s 4 red and 7 white or 5 red and 6 white, or some other combination—only that it’s more likely to be 4 and 7, for example. Then you might assign a prior distribution over the number of red balls. In that case, you would compute the probability that Bill draws the first red ball by:
Integrating (or summing) over all possible values of how many red balls are actually in the bag.
Weighting each scenario by its prior probability that the bag has that many red balls.
This becomes a Bayesian inference problem. You can write the overall probability as:
p(Bill draws first red) = sum over r [ p(Bill draws first red | r red balls) * p(r) ]
where p(r) is the prior probability that there are r red balls in the bag. A real-world example could be if you have a machine that sometimes mislabels a ball’s color, so you aren’t fully certain how many red balls ended up in the final bag.
A major pitfall is failing to incorporate the prior probabilities correctly or ignoring the possibility that r could vary. Another subtlety is updating your prior if you see new evidence (like seeing some draws are white).
What if the game stops as soon as one red ball is drawn, and all further draws are canceled?
In the standard scenario, we conceptually consider all 11 draws to be arranged, and the first red ball’s position is identified. But some real-world processes might actually stop immediately once someone draws a red.
Mathematically, these two viewpoints are the same if all permutations of the 11 balls are equally likely. The reason is that the event "the first red appears on the i-th draw" inherently ends the process for the question we care about, even if the physical game might continue in a traditional approach. So the probability that Bill draws the first red ball remains 13/33 under the assumption of uniform random arrangement.
A pitfall is to think that physically stopping changes the probability. It does not, because the random arrangement is determined at the start. Stopping early merely means you do not discover the rest of the arrangement. Unless the act of stopping somehow influences the distribution (for example, some adaptive process or knowledge gleaned from partial draws), the standard combinatorial reasoning still holds.
How do we ensure that labeling the balls and counting permutations doesn’t lead to double-counting?
A common methodological approach is to label each of the 11 balls distinctly (e.g., W1, W2, ... for the white balls and R1, R2, ... for the red balls). Then every distinct permutation of these 11 labeled balls is equally likely. When we say "the first red ball appears in position i," we don’t care which specific red ball it is among the four possible red-labeled balls—we only care that a red-labeled ball is in position i and that positions 1 through i-1 contain only white-labeled balls.
This is a robust way to avoid double-counting: each permutation is counted exactly once. A pitfall can occur if someone tries to treat all red balls as indistinguishable and all white balls as indistinguishable in some places but then inadvertently assigns permutations incorrectly in others. Mixing distinguishable and indistinguishable counting methods within the same argument can lead to confusion.
How would the probability be affected if we changed the ratio of red to white balls, but Mark still picks first?
If we have r red balls and w white balls (for a total of r + w balls), and Mark still picks first, the probability that Bill is first to draw a red ball will depend on the relative proportions of red and white. The general method stays the same, but the final numeric value, like 13/33 in the original 4-red-7-white scenario, will become a more general fraction.
One might guess that if we increase the number of red balls, it becomes more likely that the first draw (Mark’s) could be red, thereby reducing Bill’s chance. Conversely, if red balls become rarer, then it might be more likely that Bill gets the first red because multiple initial draws are white. The exact formula would involve summing probabilities that the first red ball appears on an even draw index within r + w draws. A pitfall is simply trying to plug in the numbers for one scenario into a formula that was explicitly derived for a different ratio, without adjusting the combinatorial logic properly.