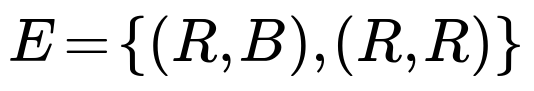ML Interview Q Series: Probability Fundamentals: Sample Space and Events for Ordered Ball Draws.

Browse all the Probability Interview Questions here.

A bag contains fifteen balls distinguishable only by their colours; ten are blue and five are red. I reach into the bag with both hands and pull out two balls (one with each hand) and record their colours.

(a) What is the random phenomenon? (b) What is the sample space? (c) Express the event that the ball in my left hand is red as a subset of the sample space.

Short Compact solution

(a) The random phenomenon is the colors of the two drawn balls (one for each hand). (b) The sample space is the set of all possible ordered pairs of colors:

(B,B), (B,R), (R,B), (R,R).

(c) The event that the ball in the left hand is red is:

(R,B), (R,R).

Comprehensive Explanation

Part (a): Random phenomenon

The random phenomenon involves choosing two balls from the bag—one in each hand—and observing their colors. Even though the draws might occur simultaneously, the left and right hands each pick a ball, so we distinguish these outcomes by which hand picks which color.

Part (b): Sample space

Since one ball is drawn in the left hand and one ball in the right hand, and each ball can be red (R) or blue (B), we must include order in our listing of the possible outcomes. That is why we have four distinct pairs:

Here, (B,R) indicates the left hand holds a blue ball while the right hand holds a red ball, and (R,B) is the opposite.

Part (c): Event: “The ball in my left hand is red”

We want the subset of the sample space where the left-hand ball is red. That corresponds to all outcomes whose first component is R. Thus:

This event captures precisely those scenarios where the left-hand ball is red, regardless of what color appears in the right hand.

Follow-up Questions

How do we know the sample space must be ordered pairs rather than unordered sets?

In many probability problems involving drawing multiple items, we have to decide whether order matters. Here, the question explicitly references the “ball in my left hand” and “ball in my right hand” as separate phenomena. Consequently, the outcome (R,B) differs from (B,R) because in the first case the left ball is red and in the second case the left ball is blue. If the problem did not distinguish the left and right hand, then we could consider unordered outcomes. But as stated, order is crucial.

What if we wanted the probability of each outcome?

If all balls are drawn randomly and without replacement, each specific pair of draws can have different probabilities. However, for color observations alone (B vs. R):

• Probability(Left = B, Right = B) is the chance that the left hand draws blue and the right hand draws blue from the remaining balls.

• Probability(Left = B, Right = R), etc.

Specifically, if you wanted the probability of (B,R) under the assumption of random drawing without replacement, you could compute:

P(Left = B) = 10/15. Then P(Right = R | Left = B) = 5/14. Hence P(Left = B, Right = R) = (10/15) * (5/14).

You would perform analogous calculations for the other outcomes.

What if we only cared about the count of red and blue in the two draws?

Sometimes, we only look at how many red balls appear in the two draws, disregarding order. In that case, the outcomes would be:

• 0 red (both blue),

• 1 red (one blue, one red),

• 2 red (both red).

But since this particular question asks for the left hand’s color specifically, we maintain the distinction between left and right.

How might you simulate this drawing process in Python?

In a real-world scenario or data-science context, you can simulate drawing from the bag:

import random

def simulate_draws(num_simulations=10_000):
    colors = ['B']*10 + ['R']*5
    results = {'(B,B)':0, '(B,R)':0, '(R,B)':0, '(R,R)':0}

    for _ in range(num_simulations):
        # Shuffle or pick randomly
        random.shuffle(colors)
        left = colors[0]
        right = colors[1]
        outcome = f"({left},{right})"
        results[outcome] += 1

    # Convert counts to approximate probabilities
    for outcome in results:
        results[outcome] /= num_simulations

    return results

print(simulate_draws(100000))

This approach creates a list of 10 blue plus 5 red balls, simulates many random draws, and tracks the frequency of each color pair. Over many iterations, you get an empirical estimate of each pair’s probability.

Are there any special considerations regarding conditional probabilities?

One subtle point is whether the act of drawing one ball in the left hand affects the probability distribution for the right hand. Because we are drawing from the same finite set of 15 balls without replacement, the events are not independent. For example, if the left hand ball is red, there are only 4 reds left among 14 total balls. This can matter if you want to compute probabilities precisely rather than just listing the sample space. Nonetheless, the sample space itself (the set of possible colors in each hand) remains the same four elements.

Could the sample space have included outcomes like (no draw) or (G, B) if there was some other color not mentioned?

No, because the problem states there are only two colors: blue and red. If there were additional colors, or if draws could fail somehow, the sample space would need to reflect those additional possibilities. As is, each ball must be red or blue, so only four ordered pairs are logically possible.

What if the problem was about counting or combinatorial formulas instead of enumerating?

Sometimes these questions appear in a form where you need to calculate the probability that both balls are red, or that at least one ball is red. In that situation, you might use combinatorial expressions:

• Probability(both red) = (5 choose 2)/(15 choose 2).

• Probability(exactly one red) = [ (5 choose 1)*(10 choose 1 ) ] / (15 choose 2 ),

and so forth. But the fundamental idea remains that for color-based outcomes, we look at the same four categories: (B,B), (B,R), (R,B), (R,R).

All of these observations reinforce how the event “ball in left hand is red” can be represented as a subset of the sample space: namely the pairs that start with R.