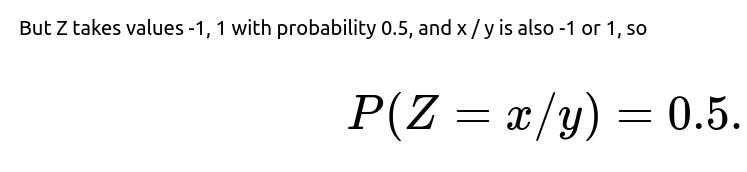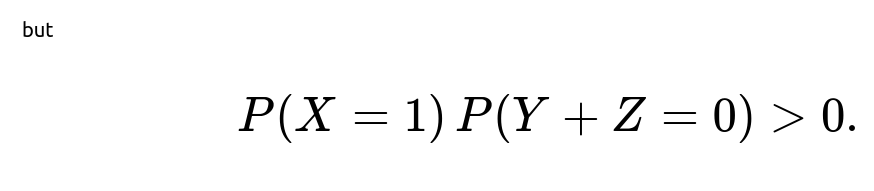ML Interview Q Series: Product of Binary Variables: Independent of Factors, Dependent on Their Sum
Browse all the Probability Interview Questions here.
Let the random variable X be defined by X=YZ
where Y and Z are independent random variables, each taking the values -1 and 1 with probability 0.5. Verify that X is independent of both Y and Z, but not of Y+Z.
Short Compact solution
Consider X and Y. For any x, y in {-1, 1},
Thus X depends on Y+Z.
Comprehensive Explanation
Independence of X and Y arises because X = YZ can be viewed as the product of Y and an independent factor Z. If Y takes values -1 or 1 with probability 0.5, and Z also takes values -1 or 1 with probability 0.5, then for any fixed y, the distribution of X given Y = y amounts to choosing Z so that X = y * Z. Since Z is equally likely to be -1 or 1, X itself is equally likely to be -1 or 1, independent of y. Mathematically, once Y is fixed to some y, the probability that X = x becomes the probability that Z = x / y, which is 0.5, so it does not depend on y at all.
If we wish to check actual joint probabilities, we can note:
P(Y = 1) = 0.5 and P(Y = -1) = 0.5.
P(Z = 1) = 0.5 and P(Z = -1) = 0.5.
Once Y = y, X = x happens only when Z = x / y, which has probability 0.5.
This leads to P(X = x, Y = y) = 0.5 × 0.5 = 0.25 whenever x, y in {-1, 1}, which matches P(X = x)P(Y = y) because P(X = x) = 0.5 and P(Y = y) = 0.5.
By a symmetric argument, X is also independent of Z. Indeed, for any z in {-1, 1}, P(X = x | Z = z) = P(Y = x / z), and once again that equals 0.5.
However, X is not independent of Y+Z because Y+Z can take values in {-2, 0, 2}, and the event X = 1 together with Y+Z = 0 never occurs. To see why, if Y+Z = 0, that means one of Y or Z is 1 and the other is -1. Then YZ = -1, so X = -1. Hence for Y+Z = 0, we must have X = -1, so P(X=1, Y+Z=0) = 0. Meanwhile, P(X=1) is 0.5, and P(Y+Z=0) = P(one is 1 and the other is -1) which is 0.5 as well. So P(X=1, Y+Z=0) = 0 while P(X=1)*P(Y+Z=0)=0.5 * 0.5=0.25, which violates the criterion for independence.
Possible Follow-up Questions
Why does the product of two ±1-valued independent random variables have a 50–50 distribution over ±1?
The key point is that for each possible pair (Y, Z), the product YZ is either -1 or 1. Since Y and Z each take ±1 with probability 0.5 independently, there are four equally likely outcomes: (1,1), (1,-1), (-1,1), and (-1,-1). Out of these four outcomes, two yield X=1 and two yield X=-1. Hence P(X=1) = 2/4=0.5 and P(X=-1)=0.5.
What if Y or Z had a different distribution than 50–50?
If Y or Z did not have an equal 0.5-0.5 split, we would need to compute the joint distribution more carefully. For example, if P(Y=1)=p and P(Y=-1)=1-p, independence from Z would still hold, but the probabilities P(X=1) and P(X=-1) could change. We would then need to verify whether P(X = x | Y = y) remains constant. In general, if Y and Z remain independent but have different distributions, X could still be independent of Y or Z under specific symmetric constraints, but it would require a direct check of the joint probabilities.
What about higher-dimensional generalizations, or if X was a function of multiple independent random variables?
We can extend this notion. If X = f(Y, Z) for some function f, independence of X from Y or Z depends on whether knowledge of Y or Z alone restricts the possible values or distribution of X. For instance, for a product f(Y, Z) = YZ, knowledge of Y alone does not constrain Z in a way that changes the distribution of the product. But if we consider a different function, such as X = Y + Z, then that might not remain independent of Y or Z. The same logic applies in higher dimensions, but the independence checks become more intricate.
How can we reason about independence of X from Y+Z in more general terms?
To show independence between two random variables W and V, we must have P(W = w, V = v) = P(W = w) P(V = v) for all w, v. If we suspect dependence, one typical approach is to identify a specific combination of events whose intersection has probability zero, but each event alone has positive probability. That is precisely what happens here: “X=1” and “Y+Z=0” cannot occur together, yet each event by itself has positive probability.
Could one approach this problem through covariance or correlation?
For ±1-valued variables, independence is stronger than zero correlation. In fact, if random variables take values ±1, zero correlation implies they are uncorrelated, but not necessarily independent. In this example, X is uncorrelated with Y or Z, yet it still remains truly independent of each. With Y+Z, it is not only correlated but actually deterministically forbidden to coincide in certain ways (X=1 cannot co-occur with Y+Z=0), which shows strong dependence. Checking correlation alone is not always sufficient to conclude or disprove independence.
These details highlight important subtleties that often arise in probability and independence questions, especially when random variables are discrete and take on limited values such as ±1.
Below are additional follow-up questions
If Y or Z are not discrete or do not have a 0.5–0.5 distribution, how does the independence argument change?
When Y or Z depart from the specific ±1 values with probabilities 0.5 each, the approach to verify independence must be more general. For instance, if Y can take different values (like -1, 1, or even other real numbers) or if the probabilities deviate from 0.5, the product X = YZ could still be independent of Y or Z, but we need to check the joint and marginal distributions more carefully.
For independence of X and Y, we still require P(X = x, Y = y) = P(X = x) P(Y = y) for all x, y in the support. If the distribution of Y or Z is not symmetric, it is possible that certain values of X become more likely given Y. In that case, the independence may break. One subtle pitfall is that even if P(X = x) = P(X = -x) for all x, it doesn’t necessarily imply the independence unless the mapping from (Y, Z) to X is symmetric in a way that preserves probabilities across all outcomes.
A real-world scenario might arise if Y and Z are measurements with non-uniform distributions (e.g., sensor outputs with skew). Even though Y and Z might be independent sensors, the functional relationship X = YZ can inadvertently carry partial information about each sensor, thus losing independence if the distributions are asymmetric.
Could partial knowledge of X = YZ reduce the possible outcomes of Y or Z in non-trivial ways?
Yes. Even if X is independent from Y in the global sense (meaning knowledge of Y does not change the distribution of X across the entire domain of outcomes), sometimes partial or “localized” knowledge might eliminate certain combinations of Y and Z. For example, if we learn that X takes a particular value combined with another event about Z, that can constrain the possible values of Y.
A subtle pitfall appears in real-time decision-making or iterative processes: if we know X from a prior step and then measure Y in the next step, we might impose constraints on Z to remain consistent with the value of X at each time. This can become complicated in dynamic systems that feed back the knowledge of X into subsequent random draws.
If we define another variable W = f(Y, Z), under what conditions is X = YZ independent of W?
In general, X will be independent of W if and only if knowledge of W does not change the probability distribution of X. Formally, for any x in the support of X and w in the support of W,
P(X = x | W = w) = P(X = x).
This hinges on how f(Y, Z) relates to the product YZ. If f(Y, Z) “factors out” the same kind of symmetry we see in YZ, then X could remain independent. For example, if W = (Y^2 + Z^2) and Y, Z only take ±1, then W will always be 2, which offers no information about X. Consequently, X and W would trivially be independent. By contrast, if W is Y + Z, as in the original scenario, that function shares certain constraints with YZ (like sign relationships), making independence fail.
An edge case arises when f is a trivial function (e.g., always returns the same constant). In that case, independence holds trivially because a constant variable has no effect on the distribution of X. But in practice, more nuanced functions can exhibit partial or complete dependence.
In practice, how do assumptions about independence in modeling lead to pitfalls?
In machine learning and statistics, one often assumes that certain features are independent for simplicity—particularly in naive Bayes classifiers or factorization approaches to joint distributions. When variables like X = YZ appear, it is easy to accidentally treat X and Y+Z as if they are uncorrelated or uninformative about each other.
A real-world pitfall could be in a scenario such as user interaction data. If Y and Z are user metrics (like “clicked vs. not clicked” and “time on site above/below average”), their product might be a composite metric representing user engagement. However, that composite could be heavily dependent on the sum or difference of the original metrics. Failing to account for this dependency can lead to incorrect probability models, poor classification performance, or misguided conclusions about user behavior.
How does this scenario relate to conditional independence?
X can be independent of Y and Z marginally, but if we condition on a third variable, we might see that the independence no longer holds. For example, if we condition on Y+Z, we already know that X is determined to be -1 if Y+Z=0. Hence, X and (Y+Z) are not independent unconditionally, but they might exhibit certain conditional relationships with Y or Z.
In some Bayesian networks or probabilistic graphical models, discovering that X is marginally independent of Y but dependent on Y+Z is a sign of “explaining away” or v-structure patterns (though not exactly in the typical sense, it’s related to how variables can become dependent once another variable is observed).
Are there situations where X remains a constant or degenerate variable under certain distributions of Y and Z?
Yes. If Y or Z take values ±1 but in a deterministic manner (for example, if Y is fixed to always be 1), then X = YZ just becomes equal to Z. In that degenerate scenario, X and Z would be the same variable, so obviously they would not be independent. Furthermore, if Y = 1 deterministically, X is basically Z, which is trivially independent of Y only if Y is indeed a constant.
A degenerate case can occur in more practical contexts if an error or design choice in data collection makes one variable unchanging. For instance, if a sensor (Y) is stuck at a certain reading and never changes due to hardware failure, the product X = YZ might effectively just replicate Z. This can cause severe confusion in feature engineering, as one might incorrectly label X as a separate feature even though it carries no novel information.
How might continuity of Y or Z affect the argument?
If Y and Z are continuous random variables taking values in (−∞, ∞) (or a subset), then X = YZ could also be a continuous variable. Independence from Y or Z would require that, for example,
P(X ≤ x, Y ≤ y) = P(X ≤ x) P(Y ≤ y) for all x, y.
The same symmetry argument can hold if Y and Z are symmetrical around 0 and independent. For instance, if Y and Z each follow symmetric distributions like a Rademacher distribution (discrete ±1, 0.5–0.5) or a continuous distribution that is symmetric about 0 (like a normal with mean 0) and if we interpret X as the product, we might preserve some symmetrical properties. But the verification is more involved because one has to evaluate integrals rather than discrete sums.
A subtlety: in continuous cases, if Y is almost surely nonzero and Z is also almost surely nonzero, then X = YZ might share partial correlation or dependence with Y or Z depending on whether the distribution is truly factorized with symmetrical shapes. Any deviation from perfect symmetry can break the independence.
Could the independence fail if Y and Z have different dependency structures across time or scenarios?
Yes. If Y and Z are only independent in certain conditions (for example, certain time intervals or subpopulations), and correlated otherwise, then even though globally you might think “Y and Z are independent,” it might not be strictly true in all conditions. Once X is formed as the product, the question of whether X remains independent from Y or Z also depends on these partial correlations.
In real-world deployments, you could have time-series data where Y and Z are independent during stable periods but become correlated during extreme events. That correlation can propagate and break the independence assumptions for X = YZ. Being aware of changes in the underlying environment (concept drift) is crucial for ensuring the independence properties remain valid.
Does symmetry guarantee independence, or are there subtler conditions?
Symmetry of Y and Z (e.g., each equally likely to be +1 or -1) is a strong reason that X = YZ becomes ±1 with equal probability 0.5. However, symmetry alone does not guarantee independence in all scenarios for more complex functions. Independence specifically requires that for each fixed value of Y, the distribution of X does not change, and vice versa.
A hidden pitfall might arise if Y and Z have symmetrical distributions but are not truly independent. If Y and Z share some hidden factor (like a time-based correlation or an underlying noise source), the product X = YZ might convey partial information about Y or Z once we learn X. Hence, verifying that Y and Z are genuinely independent is a prerequisite for X to be independent of each.