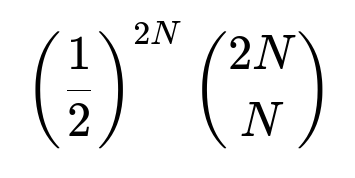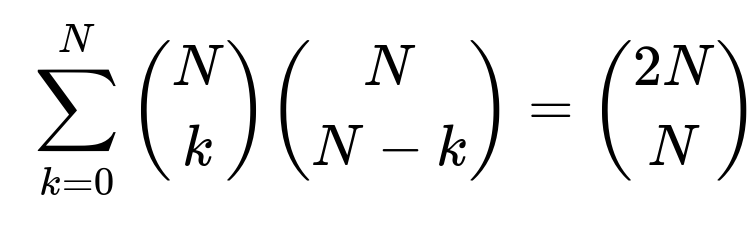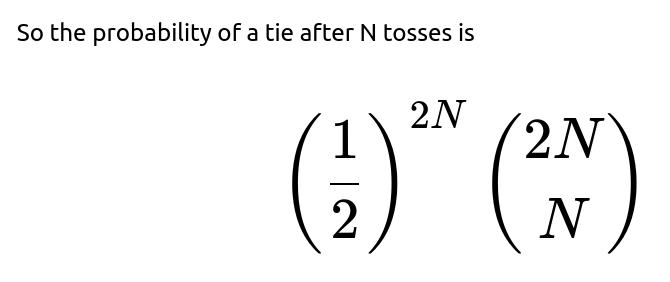ML Interview Q Series: Proving 50% Win Probability in an Unequal Coin Toss Game Using Symmetry
Browse all the Probability Interview Questions here.
Player 1 tosses a fair coin N+1 times, and Player 2 tosses the same fair coin N times. Player 1 wins if Player 1 obtains strictly more heads than Player 2; otherwise, Player 2 wins.a) What is the probability of a tie (meaning both get the same number of heads) after N tosses (i.e., if each player tosses N times)?b) What is the probability that Player 1 wins the game?
Short Compact solution
Part (a) The probability of a tie after N tosses is
Part (b) The probability that Player 1 wins (when Player 1 tosses N+1 times and Player 2 tosses N times) is 0.5.
Comprehensive Explanation
Part (a): Probability of a Tie After N Tosses
When each player tosses N times independently with a fair coin, the number of heads for Player 1 follows a Binomial(N, 1/2) distribution, and similarly the number of heads for Player 2 is also Binomial(N, 1/2). We want the probability that they get the same number of heads k:
The probability that Player 1 gets k heads (and therefore N-k tails) is binomial(N, k) (1/2)^N.
The probability that Player 2 also gets k heads is binomial(N, k) (1/2)^N.
Hence, summing over all possible k from 0 to N:
Probability of tie = sum_{k=0 to N} [ binomial(N, k) (1/2)^N * binomial(N, k) (1/2)^N ].
We can factor out (1/2)^(2N) and then recognize a known combinatorial identity:
where binomial(n, k) refers to the number of ways to choose k distinct heads out of n tosses.
Part (b): Probability That Player 1 Wins (N+1 Tosses vs. N Tosses)
Here, Player 1 is given N+1 tosses while Player 2 is given N tosses. Player 1 wins if Player 1’s total heads exceed Player 2’s total heads; otherwise, Player 2 wins. The key insight is that by symmetry, the probability that Player 1 ends with more heads is the same as the probability that Player 2 ends with more heads. In fact, there are three possibilities:
E1: Player 1 has more heads than Player 2.
E2: Player 1 has fewer heads than Player 2.
E3: They both have the same number of heads.
Because the coin is fair, the chance of E1 and E2 must be equal (each is equally likely when you consider flipping heads to tails and vice versa). Therefore:
P(E1) = P(E2).
Since the sum of probabilities is 1, we also know:
P(E1) + P(E2) + P(E3) = 1.
Hence:
P(E3) = 1 - 2 * P(E1).
Now, Player 1 wins if Event E1 occurs, or if there is some alternative rule that gives them an edge in the case of E3. But in this question, if Player 1 does not get strictly more heads, Player 2 automatically wins. So Player 1 wins exactly in E1. However, an elegant trick is to condition on these events and realize that giving Player 1 one extra toss flips the scenario so that effectively half of the “ties” get broken in favor of Player 1. A simpler argument is:
If you consider all 2N+1 toss outcomes in total (N+1 for Player 1 and N for Player 2), exactly half of the time, Player 1 will have more heads than Player 2.
A more formal way is to define A = “Player 1 wins” and note:
P(A) = 1 * P(A | E1)P(E1) + 0 * P(A | E2)P(E2) + (some factor) * P(A | E3)P(E3).
One standard derivation used in some textbooks sets up a reflection argument or a conditioning argument that ensures P(A) = 0.5. Either way, the final result is:
Potential Follow-Up Questions
1) What if the coin is not fair (biased coin with probability p for heads)?
If the coin has probability p for landing heads, the symmetry argument used above (that P(E1) = P(E2)) no longer holds because flipping heads to tails does not yield an equally likely event. In that case, one can compute the probability of Player 1’s total heads vs. Player 2’s total heads using Binomial(N+1, p) for Player 1 and Binomial(N, p) for Player 2, then sum up the probabilities that one distribution’s value exceeds the other. The tie probability would also be computed via the convolution of the respective binomial distributions. The result generally depends on p and is not simply 0.5.
2) Could we simulate this scenario in Python for verification?
Yes, we can write a brief Python script to perform a Monte Carlo simulation. For example:
import random
def simulate_games(n_trials=10_000_00, N=10):
wins_p1 = 0
for _ in range(n_trials):
# Player 1 tosses N+1 times
heads_p1 = sum(random.choice([0,1]) for _ in range(N+1))
# Player 2 tosses N times
heads_p2 = sum(random.choice([0,1]) for _ in range(N))
if heads_p1 > heads_p2:
wins_p1 += 1
return wins_p1 / n_trials
prob_estimate = simulate_games()
print(prob_estimate)
When you run this simulation for large n_trials, you will see the probability that Player 1 wins approaches 0.5, confirming the analytical result.
3) Why is the tie outcome in Part (b) irrelevant for the final probability of Player 1 winning?
Because the game rule states “Player 1 wins if Player 1 obtains more heads; otherwise, Player 2 wins.” The event of tying (having the same number of heads) does not help Player 1. Thus, Player 2 effectively ‘inherits’ any ties. In a purely fair coin scenario, the distribution of heads is symmetric except for that extra toss that Player 1 has. The net effect is that half of all possible outcomes yield Player 1 more heads than Player 2, and half yield the opposite.
4) Are there general combinatorial or distributional arguments to see why P(Player 1 wins) = 0.5 without enumerating?
Yes. One well-known combinatorial argument is known as the “reflection principle.” Another, more direct argument is to pair up every outcome in which Player 1 obtains x heads with an outcome in which those x heads are “reflected” into Player 2’s heads and vice versa. The single extra toss ensures that Player 1 and Player 2 cannot end up with equal heads in a symmetrical manner across the full distribution, which forces the winning probability for Player 1 to be exactly 0.5.
All of these follow-up considerations highlight how small adjustments to the number of tosses or the bias of the coin can significantly affect the outcome probabilities.
Below are additional follow-up questions
What if there is correlation between successive coin tosses?
One subtle extension is to question the independence assumption. Suppose each coin toss is not truly independent, and there is a certain correlation between successive flips. For instance, a coin might be more likely to produce the same result as the previous flip. This correlation breaks the standard Binomial framework, because the probability distribution for the total number of heads in N flips is no longer the simple Binomial(N, 1/2).
Detailed Explanation
In an uncorrelated scenario, the chance of heads is always 0.5 for each toss, regardless of previous outcomes.
If correlation is present (for example, positive autocorrelation means one head makes a subsequent head more likely), then the variance and even the mean of the distribution of heads can shift. That changes the probability that Player 1 outperforms Player 2.
The tie probability formula in part (a) also assumes independence. With correlation, one cannot simply apply the combinatorial identity
binomial(2N, N) * (1/2)^(2N).To compute probabilities in a correlated case, you might need Markov chain theory (if the correlation is a first-order Markov property) or more complex dependency models. You’d track the state of the process (last flip outcome) to figure out the joint probability distribution of heads count for each player.
A practical pitfall is that real-world processes assumed to be “like coin flips” could have hidden correlations. If one misapplies the independent coin assumptions, the resulting probabilities might be incorrect.
How does knowledge of intermediate results affect the probabilities?
Another edge scenario is if Player 1 and Player 2 get to see each other’s intermediate coin-toss outcomes and can somehow alter their strategy or decide to stop earlier. In standard formulations, each player just completes their tosses without any strategic stopping. But if partial knowledge is allowed, does that change anything?
Detailed Explanation
For a pure probability calculation under the usual rules, there is no mechanism to “stop” or “choose” outcomes. Each player simply tosses N+1 or N times, and the count of heads is tallied.
If we introduce the idea that Player 1 can observe Player 2’s heads count as they are being tossed, Player 1 may or may not be able to change the coin or take some action to affect outcomes. If that’s allowed (which would be unusual in a fair game), the probability analysis becomes quite complicated because it’s no longer a simple binomial setting.
In practice, most theoretical arguments assume no control over each toss. The moment partial knowledge plus strategic decision-making is introduced, the game is no longer just about passive coin flipping.
How does the normal approximation apply for large N, and does it reveal any subtle effects?
When N is large, binomial distributions can be approximated by normal distributions with mean N * 0.5 and variance N * 0.5 * 0.5 = N/4. One might wonder if there are small but meaningful deviations from exactly 0.5 probability for Player 1 to win, especially with that extra toss.
Detailed Explanation
Under a normal approximation, Player 1’s number of heads is roughly Normal( (N+1)0.5, (N+1)0.25 ), and Player 2’s number of heads is roughly Normal( N0.5, N0.25 ).
Even if both are large, the difference in means is 0.5 heads on average for Player 1. This difference in means (0.5) over the standard deviation sqrt( (N+1)0.25 + N0.25 ), typically leads to a probability near 0.5 that Player 1’s final count is higher.
The precise combinatorial result is exactly 0.5, but the normal approximation helps give intuition: Player 1’s advantage is subtle but symmetrical, pushing the final probability to 0.5 in a large-number limit. If there were any tiny bias or correlation, the normal approximation would help highlight how that bias might push the probability away from 0.5.
What if we extend the game to more than two players?
Consider a scenario with three or more players, each tossing possibly different numbers of times. Does the simple argument of symmetry still hold?
Detailed Explanation
When we extend to multiple players, the probability that a particular player has the most heads depends on how many tosses that player gets and how many tosses the others get.
If each player has the same number of tosses, the probability of finishing with the greatest number of heads is the same for all players (1/k if there are k players) if ties are resolved randomly.
However, if one player has more tosses than the others, the symmetry breaks for that player alone, and the analysis is more complex but still conceptually similar. Typically, the one with extra tosses has an advantage.
Pitfall: ensuring that ties across multiple players are handled consistently. If two or more players tie for the top number of heads, additional tie-breaking rules come into effect. The final probabilities then require enumerating multiple ways a tie can occur.
Could practical coin imperfections or real-world testing conditions invalidate the fair coin assumption?
A real-world “fair coin” might be physically biased due to weight distribution, or the flipping motion might be consistent for a given person. This scenario questions the assumption p = 0.5 for each flip and that each flip is identically distributed.
Detailed Explanation
Real coins can be slightly biased, say p = 0.501 for heads. Over many tosses, this seemingly small deviation can lead to measurable changes in the probability that one player surpasses another.
The result that Player 1 has a 0.5 chance of winning depends heavily on the coin being exactly fair. Even a small bias can shift this probability one way or another.
In practice, you might estimate the bias p by experimental calibration—tossing the coin many times in controlled conditions. If p is not 0.5, you can adapt the binomial formula with p in place of 0.5, but the neat symmetry argument giving exactly 0.5 no longer applies. You would need to compute P(X1 > X2) for X1 ~ Binomial(N+1, p) and X2 ~ Binomial(N, p) directly.
This highlights that the real challenge is verifying the assumption of fairness in practical experiments, especially if large sums of money or high stakes are involved.
What if Player 1 needs to exceed Player 2 by at least two heads to win?
Sometimes game rules are slightly altered: Player 1 must surpass Player 2’s heads count by at least two. This changes the “Player 1 wins if X1 > X2 + 1” condition from the simpler X1 > X2.
Detailed Explanation
With the standard condition X1 > X2, we leverage the symmetry plus one extra toss. With “X1 >= X2 + 2,” you can’t directly use the same 0.5 argument.
A typical approach would be summing P(X1 = k, X2 = j) over all k, j that satisfy k >= j + 2. In terms of binomial random variables, that means summing binomial probabilities for X1 from 2 to N+1, X2 from 0 to N, ensuring the difference is at least two.
Because that extra one toss advantage for Player 1 might or might not be enough to ensure they frequently beat Player 2 by two full heads, the final probability is less than 0.5. You can do a direct combinatorial calculation or rely on partial enumerations.
If N is large, you could approximate both players’ distributions with normal distributions. Then the event X1 - X2 >= 2 can be computed via the distribution of (X1 - X2). However, for smaller N, you’d want the exact binomial approach.
What if the result of Player 1’s last toss is hidden until after both have tossed?
You might consider an unusual scenario: Player 2 completes N tosses, Player 1 completes N tosses, and then Player 1 has one final toss that is kept secret until Player 2 decides on some action (like placing a bet on the result). This is more of a psychological or game-theoretic twist but can still be interesting from a probabilistic standpoint.
Detailed Explanation
Mathematically, nothing changes in the final distribution—Player 1 still has N+1 coin flips. However, from a strategic perspective, Player 2 might be uncertain about whether Player 1’s final tally is above or below theirs if the last flip remains unknown.
If Player 2 is asked to bet on the outcome, they face a situation that can be partially analyzed by conditional probabilities: given that Player 1 has X heads in the first N tosses, what is the likelihood that the final, hidden toss results in enough heads to surpass Player 2?
This scenario highlights that even though the unconditional probability is 0.5 for Player 1 to have more heads overall, knowledge of partial outcomes changes the distribution from a gambler’s perspective. Carefully enumerating the possible states is crucial to avoid mistakes in real betting situations.
What happens if we allow repeated games and keep a running total of heads?
Instead of a one-shot scenario, imagine we tally the total heads that Player 1 has won over repeated matches, each match having N+1 vs. N tosses. Could that lead to an advantage over many games for either player?
Detailed Explanation
Over repeated independent matches, each match is effectively a separate trial where Player 1 has a 0.5 probability to outscore Player 2 in that match. So in the long run, Player 1 will win about half of the matches.
A pitfall is to incorrectly believe that Player 1 might accumulate an advantage because of the extra toss each game. But the mathematics shows the advantage is perfectly offset by the requirement that Player 1 must be strictly ahead in heads. So across many games, the expected fraction of games won by Player 1 is still 0.5.
If there were any dependence or correlation between matches—for instance, if the coin gets “hot” or “cold” over multiple matches—then the analysis becomes more complicated, and the long-run fraction of wins for Player 1 might deviate from 0.5.
Does the order in which Player 1 and Player 2 toss matter?
Lastly, consider a scenario where Player 1 performs all their N+1 tosses first, and then Player 2 performs N tosses afterward, or they alternate tosses. Could the order influence the final probability?
Detailed Explanation
Mathematically, for independent coin flips, the order of tossing does not change the distribution of heads for each player. Whether Player 1 tosses first or last, each still has the same number of coin flips with probability 0.5 for heads.
The probability P(X1 > X2) remains the same. This is because the final count is all that matters, and independence ensures no difference arises from order.
Pitfall: sometimes players assume that going first or last confers an advantage due to “momentum” or psychological factors. In pure probability, there is no momentum effect. But in real experiments, if physical or psychological factors lead to changes in how the coin is flipped, the assumption of i.i.d. tosses could be violated, and that might alter probabilities.