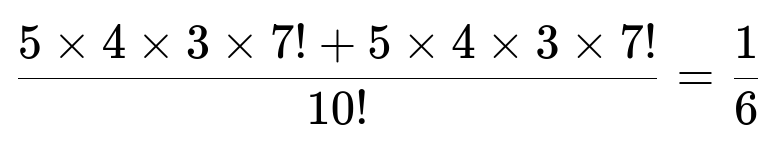ML Interview Q Series: Random Group Splits: Probability of Friends Staying Together Using Combinatorics.
Browse all the Probability Interview Questions here.
You and two of your friends are in a group of 10 people. The group is randomly split into two groups of 5 people each. Specify an appropriate sample space and determine the probability that you and your two friends are in the same group.
Short Compact solution
One way is to consider an ordered sample space of all 10! permutations of the 10 individuals. In this view, the first 5 individuals in each permutation form one group, and the other 5 form the second group. Then the probability that you and your two friends end up in the same group is given by summing the number of permutations that place all three of you in the first group plus the number of permutations that place all three of you in the second group, and dividing by 10!. This yields:
Alternatively, consider an unordered sample space where each outcome is a choice of 5 people out of 10 to form the first group. The probability becomes:
Hence, the probability that you and your two friends are all together is 1/6.
Comprehensive Explanation
Understanding the Sample Space
There are two common ways to define the sample space:
1) Ordered sample space:
We count all possible orderings (permutations) of the 10 individuals. There are 10! total permutations.
In each permutation, the first 5 listed form one group, and the remaining 5 form the other group.
Because each ordering is assumed equally likely, the probability of any specific configuration of two groups of 5 is the fraction of the total permutations that produce that configuration.
2) Unordered sample space:
We consider all ways to choose any 5 people out of 10 to form one group (and the other 5 go to the second group).
The total number of ways to choose which 5 go into the first group is C(10,5). Each such choice is assumed equally likely.
In both cases, we should get the same final probability.
Ordered Sample Space Approach in Detail
If we label you as A, and your two friends as B and C, then:
To put A, B, and C in the first group of 5, first place A, B, and C in 3 of the 5 positions of that first group. There are 5 x 4 x 3 ways to assign them specific positions if we treat the first group as positions 1 through 5 in the ordering.
The remaining 2 positions of that first group are filled by any 2 of the remaining 7 people, and then the other 5 people (the leftover 5 from the 7) occupy the second group, but also can permute among themselves.
Similarly, there is an equally large count for the scenario where A, B, and C are together in the second group of 5.
When all those permutations are summed, and the total is divided by 10!, we get 1/6.
Unordered Sample Space Approach in Detail
We can think directly about how the final groups of 5 form:
The total number of ways to pick 5 out of 10 is C(10,5). This counts all possible distinct 5-person teams you might label as the “first” group.
To have A, B, and C all together in the first group, we must choose all three friends plus any 2 out of the other 7 people. That is C(7,2) ways.
There is an equally valid scenario in which A, B, and C are all in the second group. By symmetry, that also corresponds to C(7,2) ways of forming the first group without the three friends (equivalently, if the first group is chosen from the 7 people excluding A, B, and C, that’s C(7,5) ways, which is the same value as C(7,2)).
Summing the favorable cases for either group, and dividing by C(10,5), results in 1/6.
Why the Probability is 1/6
A more intuitive view is to think about placing your two friends after you have already been placed in some group. There are 9 remaining slots (after you occupy 1 of the 10). Of those 9 slots, 4 slots belong to the group you are in, and 5 slots belong to the other group. The probability that both friends land in those 4 “same group” slots (rather than being split or placed entirely in the other group) can be computed as:
Probability that friend 1 also joins your group: 4/9
Conditional probability that friend 2 also joins your group given friend 1 is in it: 3/8
Hence the combined probability is (4/9) x (3/8) = 12/72 = 1/6.
This approach is often the most straightforward: once you fix yourself in a particular group, the question reduces to whether your two friends both land among the 4 open spots in that same group.
Potential Follow-Up Questions
What if the groups were of different sizes?
If one group had size k and the other had size 10 - k, the total number of ways to choose which group you end up in and how your friends are placed changes slightly. You could analyze it by:
Considering the probability that your two friends also land in your group of size k, which involves (k - 1)/(10 - 1) for the first friend and (k - 2)/(10 - 2) for the second friend, provided both are placed after you are fixed in that group.
Or by counting combinations directly using C(9, k - 1), where we pick who joins you in the smaller group, and so on.
The overall logic is the same but with adjusted group size.
What if we want the probability that exactly two of you are in the same group?
You would count scenarios where exactly you and one friend are together (and the other friend goes to the other group), divided by the total ways of forming two groups of 5. You could approach this using combinatorics. For example, fix yourself in one group, count ways one friend joins you but not the second, then similarly for the other group, and so forth. Always confirm that the final count reflects all valid ways in the sample space.
How would you implement a quick check in Python?
One simple check is by simulation. For instance:
import math
import random
def simulate_groups(num_simulations=10_000_00):
count_same_group = 0
for _ in range(num_simulations):
# We have 10 people, of which 3 are special (you + 2 friends)
people = list(range(10))
random.shuffle(people)
# First group is first 5, second group is next 5
group1 = set(people[:5])
group2 = set(people[5:])
# Suppose the special individuals are labeled 0, 1, 2
if (0 in group1 and 1 in group1 and 2 in group1) or (0 in group2 and 1 in group2 and 2 in group2):
count_same_group += 1
return count_same_group / num_simulations
prob_estimate = simulate_groups()
print(f"Estimated probability: {prob_estimate}")
Over many runs, the estimate should converge close to 1/6.
This kind of simulation can be used to verify other more complicated scenarios quickly and is a powerful technique in data science and machine learning when dealing with probability questions that are too complex for a direct combinatorial or closed-form approach.
Below are additional follow-up questions
What if we want the probability that at least two of you end up in the same group, rather than all three?
To tackle this, we note that “at least two” means either exactly two of the three friends end up together or all three end up together. One approach is to calculate the complement event (none of you are in the same group, which is actually impossible with only two groups if you are all distinct individuals) or more sensibly, compute directly the probabilities for exactly two in one group and the third in the other group, plus the probability that all three are together.
Detailed Reasoning
Probability(all three in the same group): We already know this to be 1/6.
Probability(exactly two together and one separate):
First, choose which 2 friends end up with you. That choice is among the three possible friend-pairs.
Then, consider you and those 2 friends form a partial subset of size 3 in a 5-person group, and the remaining 1 friend ends up in the other group. We can count this using combinatorial arguments similar to the original solution.
Alternatively, we can do a direct distribution approach: Fix yourself in one group, you have 4 remaining spots in your group and 5 spots in the other group. The probability that exactly one of your two friends joins your group is:
Probability that a specific friend joins your group is 4/9, and the probability that the other friend goes to the other group is 5/8, so 4/9 × 5/8.
Since there are 2 choices for which friend is in your group, multiply by 2. That yields 2 × (4/9 × 5/8) = 2 × (20/72) = 40/72 = 5/9.
But this 5/9 includes the scenario of “two friends are exactly split between the groups,” ignoring the possibility that you end up with none or all. We must be consistent in including all relevant cases.
Adding it up for “at least two”: We combine the probability for exactly two plus the probability for three. Carefully check we include the correct sets of outcomes without overcounting. In many combinatorial probability questions, enumerating complements or employing direct partition counts (grouping cases) is a safer route to avoid double counting.
Potential Pitfalls
Forgetting that “none in your group” might be possible if the groups are uneven or if there are more than two groups. In our basic scenario, if you are in one group, at least one friend must be in one of the two groups—there is a possibility all your friends could be in the other group, but that’s separate from “none in your group.” Always confirm the partition logic.
Mixing up the approach for exactly two vs. at least two can lead to double counting. Sometimes, it is clearer to use the complement principle (like 1 – Probability(all three together) – Probability(all three in completely separate groups)), but that also can be tricky if there are only two groups.
How does the probability change if we introduce more than two groups?
When dividing 10 people into multiple groups (e.g., three groups of different sizes or equal sizes), the straightforward 1/6 result no longer applies. You now have more partitions to consider, and the event “all three of you land in the same group” changes in probability according to how those groups are sized and how they are formed.
Detailed Reasoning
Number of ways to partition 10 people into multiple groups: The count depends on whether the groups are distinct (like Group 1, Group 2, Group 3) or not. This can get complicated quickly.
Placing your trio in one of these multiple groups: If each group has size k1, k2, ..., you can do a direct counting argument: pick which group the trio goes into (provided it can fit all three), then choose who else goes into that group, and distribute the remaining people among the other groups.
Probability approach using sequential placement: Another method is to fix your own position, then measure the chance the two friends join the same group. However, you must carefully consider the total number of slots in each group and the order in which those slots are filled.
Potential Pitfalls
Over-counting partitions if groups are labeled vs. unlabeled. Partitions into unlabeled groups must be treated with special attention to avoid multiplying by permutations of identical groups.
Different group sizes can lead to drastically different probabilities (e.g., having a 7-person group and two 1-person groups can significantly increase or decrease certain probabilities relative to the balanced scenario).
How does the analysis change if people are grouped with a bias (not purely random)?
Sometimes a “random” grouping is not truly uniform: maybe there is a preference or constraint like ensuring certain people aren’t placed together, or certain people must always be grouped together. In such cases, the assumption of equally likely configurations is violated.
Detailed Reasoning
Modeling the bias: One could represent constraints or preferences via a weighted probability model over all possible ways to form the groups. Instead of each arrangement being equally likely, each arrangement might have a probability proportional to some weighting function.
Calculating probabilities with constraints: Often we must enumerate or sample from the constrained set of group partitions, or solve a combinatorial optimization problem subject to constraints.
Simulation approach: If the weighting or constraints are too complex to handle analytically, a Monte Carlo simulation can approximate the probability that you and your two friends end up together.
Potential Pitfalls
Assuming uniform probability inadvertently when constraints create a non-uniform distribution. This leads to incorrect results.
Not realizing that certain group formations might be impossible under the constraints (like “friend A and friend B can’t be in the same group”), which changes the sample space drastically.
What if you only know partial information about how the groups were formed?
Sometimes you only know that you ended up in a certain group, but you do not have full knowledge about how the rest of the group was decided. Maybe you learned that half the group were chosen from a special subset of the 10 people. The probability that your two friends joined you can shift based on this partial information.
Detailed Reasoning
Conditional probability: Suppose you know that you are in a particular group. You might also know one friend was definitely placed in a certain subgroup or had to be placed with certain people. Then you must adjust the probability accordingly to account for this new information.
Bayes’ theorem approach: If partial data is available (e.g., “We know friend B is in the same group as person X”), you can incorporate that knowledge to update your belief about where B and C likely ended up.
Incomplete data: In some real-world scenarios, you might only observe the final group composition partially or have uncertain membership. Then you might estimate the probability by enumerating all consistent configurations or by employing a Bayesian method with prior assumptions on how groups were formed.
Potential Pitfalls
Double counting or ignoring configurations not consistent with partial observations.
Overlooking correlations (maybe the presence of certain people in your group indicates your friends might be more or less likely to join).
How might you extend this to more than three friends?
If you and N friends (out of the total 10) want to be together, the basic approach of combinatorial counting remains, but the formula changes. Instead of focusing on 3 people together, you now want a group containing all N of you, plus the remaining group size minus N from the rest.
Detailed Reasoning
Unordered approach: The probability that all N of you end up in the same group of size 5 out of 10 is C(10 - N, 5 - N) / C(10, 5). But you also have the possibility you all end up in the other group, so you multiply by 2 if the other group is also size 5.
Ordered approach: Similarly, you can count permutations that place N of you within the first 5 positions or the second 5 positions in a 10! ordering.
Constraints on group size: Note that if N > 5, you can’t all be in the same group. So if N = 6, for instance, the probability is 0. Always confirm that the scenario is actually possible.
Potential Pitfalls
Neglecting the fact that N might exceed the group size. If you have 6 or more people trying to stay together in a group of 5, the event is impossible.
Failing to include symmetrical cases: being in the “first group” vs. the “second group” can each offer valid outcomes.
What if the split is not always exactly 5 and 5?
In practical settings, the group split could occasionally be 6 and 4, or 7 and 3, etc. Or maybe the total group size is larger, and exactly 10 is a subset. This complicates direct application of the 1/6 result.
Detailed Reasoning
Random variable group size: If the size of each group is itself random (e.g., sometimes 5–5, sometimes 6–4, etc.), you must weight each scenario by the probability that the split is that size.
Conditional calculations: Condition on the group-size scenario: Probability = sum over each split size [Probability(all three together | split size) * Probability(of that split size)].
Practical example: If it’s 6–4 with probability p and 5–5 with probability 1 – p, you calculate the probability of being together for 6–4 and for 5–5 separately, then do a weighted sum.
Potential Pitfalls
Overlooking how the random size is chosen. Is it equally likely to have 6–4 vs. 5–5? Or is the random split decided in some other manner? The distribution assumptions matter.
Attempting to reuse the old formula 1/6 blindly. That result is specific to 5–5 splits.
How do we handle overlapping circles of friends?
Consider you have three friends you want to stay with, while another subset of the group has their own set of individuals that also want to stick together. The events may overlap if some individuals belong to multiple friend circles. This leads to more intricate probabilities.
Detailed Reasoning
Intersecting events: The probability that your trio stays together and another pair stays together is not simply the product of their independent probabilities (which would be the case if these events were independent). You must account for the overlap.
Count or use the inclusion-exclusion principle: If you want the probability that both friend circles remain intact in the same group, you might do a direct enumeration of how each circle can be placed in the partition. Or apply inclusion-exclusion if you only want the union of events (e.g., the probability that your trio is together or the other pair is together).
Real-world complexity: Often, teams in real-life may have multiple constraints. Some people want to stay together, others want to be separate, and these constraints can pile up. The purely random model no longer applies, and a systematic counting or simulation approach is needed.
Potential Pitfalls
Treating multiple friend circles as if they don’t overlap. If a person is in more than one circle, you can’t just multiply the separate probabilities.
Double counting configurations where both conditions are satisfied.
Could you map this to a graph-theoretic perspective?
Sometimes grouping people is analogous to partitioning a graph into subgraphs. For instance, a “friendship link” might mean two people want to be in the same group. The question becomes: “What is the probability that a certain subgraph (triangle, representing you plus two friends) is contained entirely within one of the partitioned subgraphs?”
Detailed Reasoning
Graph partition interpretation: Construct a graph with each person as a node. An edge between two nodes might indicate a desire to be in the same group. When you randomly split the nodes, you effectively color them with two colors (for two groups). The question of all three being in the same group is the question of them having the same color.
Edge constraints: If you have multiple edges, you might ask for the probability that all edges among certain nodes end up “monochromatic.” This is related to random graph colorings.
Extensions to more sophisticated scenarios: If you have weighted edges or partial preference, you could assign probabilities or costs to each coloring and compute the partition distribution accordingly.
Potential Pitfalls
Overcomplicating a basic problem by introducing graph concepts, especially if you only need the classic combinatorial approach. However, for advanced constraints or multiple friend sets, graph-based modeling can be very useful.
Assuming independence among edges. In grouping scenarios, membership constraints can correlate edges in non-trivial ways.
How might we estimate the probability if the total group size is very large (e.g., 1000 people) and we want to randomly form smaller teams?
When numbers grow large, the direct combinatorial approach is still valid but can be computationally intensive. We often look for approximations or asymptotic results.
Detailed Reasoning
Asymptotic approximation: If we fix the group size at n and let the total population go to N with n << N, the probability that all your friends are in the same group often approaches a limit related to (n/N)^{(k-1)} if you have k total friends.
Poisson binomial or occupancy models: In more complex settings, distributing N individuals into multiple groups is akin to a “balls into bins” process. The probability that certain individuals end up in the same bin can be approximated by ignoring small correlations if N is huge.
Monte Carlo simulation: Generating random subsets for large N is feasible with a computer, and we can approximate the probability very accurately if combinatorial calculations become unwieldy.
Potential Pitfalls
Relying blindly on large-N approximations for moderately sized N (like 10 to 50) can produce errors if not checked for accuracy.
Implementation details for simulation: ensuring random sampling is uniform and that you handle memory constraints if N is very large.
How do we verify our combinatorial probability in practice?
In real-world scenarios, you might repeatedly sample or observe actual group formations. Then you’d estimate the probability that your trio ends up in the same group from empirical data. You can compare that with the theoretical 1/6 result to confirm alignment (or reveal biases in group assignment).
Detailed Reasoning
Empirical frequency: Suppose you see 1000 random splits of the 10 people. If 170 out of 1000 times your trio is together, that’s an empirical estimate of 0.17. The ideal is 1/6 ≈ 0.1667, so the empirical result is close.
Statistical confidence intervals: You can compute confidence intervals around your empirical frequency. For a binomial process with p=1/6, a sample of 1000 trials yields a 95% confidence interval that could be used to see if your data significantly deviates from the theoretical value.
Practical usage: This kind of empirical check is common in scenarios where the actual process might differ from the theoretical assumptions.
Potential Pitfalls
If the actual group formation mechanism is not uniform random, an empirical estimate will systematically deviate from the theoretical 1/6.
Stopping the experiment after only a few trials can lead to large sampling errors or incorrect conclusions.