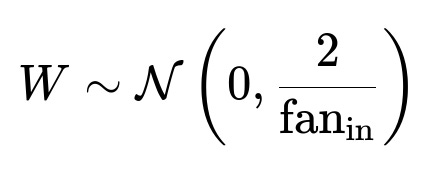ML Interview Q Series: Random Weight Initialization: Breaking Symmetry for Effective Neural Network Training.

📚 Browse the full ML Interview series here.

27. Is random weight assignment better than assigning the same weights to units in the hidden layer? Why or why not?

Random weight initialization is generally better than assigning the same weights to all units in a hidden layer because randomization breaks symmetry. When all neurons in a layer start with identical weights, each neuron performs the same computations and receives identical gradient signals, preventing them from learning unique features. Random initialization ensures that neurons develop distinct activation patterns, enabling the network to learn complex relationships in data. By giving slightly different initial parameters to each neuron, gradient-based learning methods (such as backpropagation) can tailor weights to extract a variety of features, thus improving the model’s performance.

When we assign the same weight to all neurons in a hidden layer, we lose the diversity in their outputs and derivatives. This lack of diversity causes the same gradient updates to be applied to each neuron’s weights. With random initialization, the distribution of weights is not uniform, and each neuron can potentially learn specialized aspects of the input. Over time, these variations allow the network to converge to a useful set of parameters that captures different patterns in the data.

In more detail, consider a single hidden layer neural network. If each weight is initialized to the same constant cc, each neuron receives the same weighted input and produces the same activation. The gradient with respect to the weights of each neuron would be identical. This makes training no better than training a single neuron repeatedly and copying it to multiple places. By introducing randomness in weights, each neuron starts with a different transformation of the inputs, leading to different gradient signals that allow each neuron to update in unique ways.

What does “symmetry breaking” mean in this context?

Symmetry breaking refers to the process of preventing neurons (or other parameters) from being identical during training. If neurons start identically and receive identical gradient updates, they will remain identical throughout training. Breaking this symmetry—by ensuring different neurons have slightly different initial parameters—enables each neuron to capture a different aspect of the input distribution.

Could I ever benefit from assigning the same weight to all hidden units?

In most modern deep learning applications, you rarely benefit from setting all hidden units to the same weight. The only times you might use constant initialization are for specialized settings such as biases (often initialized to a small constant like zero or 0.01) or specific normalization layers (which might initialize scale parameters to 1). Even in those cases, the main network weights are still given a random distribution because that is crucial for effectively training the model and ensuring diverse feature learning.

How does random initialization help with gradient-based learning?

Are there preferred distributions for random weight initialization?

Researchers have found that certain distributions make training more stable and efficient. Although it is called “random initialization,” in practice, many frameworks use carefully chosen distributions or scaling factors. Two common methods are Xavier (Glorot) initialization and He initialization:

Xavier initialization. This scales weights based on the number of inputs and outputs of a layer so that the variance of activations and gradients are maintained in a reasonable range. Typically, the initialization is something like

or in a uniform equivalent. Here, fan_in is the number of input units for the layer, and fan_out is the number of output units. This keeps signals from blowing up or vanishing too rapidly.

He initialization. This is commonly used for ReLU activations, since ReLUs zero out half of their input space on average. It also looks at the number of inputs and uses a factor of 2:

These approaches ensure the network starts off with activations and gradients at scales that foster stable learning. Straight-up uniform random or Gaussian initializations without proper scaling can sometimes lead to gradients that explode or vanish more readily, slowing or sabotaging learning.

How can I implement random initialization in PyTorch or TensorFlow?

Most deep learning frameworks handle random initialization automatically. For example, in PyTorch you can define a layer and let PyTorch set the parameters by default initialization or you can manually initialize them. In PyTorch:

import torch
import torch.nn as nn

class SimpleNet(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(SimpleNet, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, output_dim)
        # Optional: You could override the default initialization below:
        nn.init.xavier_uniform_(self.fc1.weight)
        nn.init.zeros_(self.fc1.bias)
        nn.init.xavier_uniform_(self.fc2.weight)
        nn.init.zeros_(self.fc2.bias)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = self.fc2(x)
        return x

By default, PyTorch already uses variants of Kaiming (He) uniform initialization for linear layers. If you want a different method, you can explicitly set it after layer creation, as shown above. Similarly, in TensorFlow Keras you can choose an initializer in a layer definition:

import tensorflow as tf

model = tf.keras.Sequential([
    tf.keras.layers.Dense(64, activation='relu',
        kernel_initializer=tf.keras.initializers.HeUniform(),
        bias_initializer=tf.keras.initializers.Zeros(),
        input_shape=(input_dim,)),
    tf.keras.layers.Dense(num_classes, activation='softmax',
        kernel_initializer=tf.keras.initializers.GlorotUniform(),
        bias_initializer=tf.keras.initializers.Zeros())
])

Either way, the primary objective is to ensure that each neuron starts with distinct weight values that still keep the forward and backward signals in stable ranges.

What if I use methods like batch normalization? Does initialization matter as much?

Batch normalization helps mitigate issues such as exploding or vanishing gradients by normalizing activations within each mini-batch. While it can make training less sensitive to weight initialization, you generally still want to break symmetry with random initialization. Batch normalization will not fix the fundamental problem of all neurons being identical if you started them all at the same point. It only regulates the distribution of activations, not the underlying weight diversity. So random initialization combined with batch normalization remains standard best practice.

Are there any rare situations where constant initialization could make sense for weights?

In nearly all typical neural architectures, constant initialization of weights is detrimental. The only context where constant initialization might make sense is in contrived scenarios, such as establishing a simple proof-of-concept demonstration where you do not actually intend to learn from data in the usual sense. Even then, the model might not train effectively.

Occasionally, researchers experiment with special layers that contain parameters set to constants (for example, in some normalization layers), but those constants are not trained in the same way as a standard weight matrix for a hidden layer. Also, bias terms can sometimes be set to a constant like 0 or 0.01, but that is a separate consideration from weight initialization.

Could advanced weight tying or parameter sharing contradict the idea of random weight initialization?

Weight tying or parameter sharing is a technique used in models like certain RNN or transformer architectures (such as tying input and output embedding layers). This is not the same as giving all neurons in a hidden layer the same initial weights. In weight tying, two or more layers are forced to share the same parameters for representational or efficiency reasons. However, you still typically perform some form of random initialization on those shared parameters. The concept of symmetry breaking still applies within the context of the rest of the network. You do not initialize everything in that entire architecture to the same constant; you just designate that specific layers share identical parameters for a particular reason. This is done in a controlled manner, and each shared parameter set still starts with a random distribution so that training can learn effectively.

Is there a difference between random initialization and random re-initialization?

In normal training, you randomly initialize the weights once before beginning training. Random re-initialization would mean repeatedly resetting weights to random values during training—this is generally not done except in experiment-driven contexts such as hyperparameter tuning or as a strategy to escape poor local optima in extremely challenging scenarios. Most standard training loops do not re-initialize random weights after the initial setup because you would lose all the learned progress in parameters each time you re-initialize.

What are some common pitfalls if I forget to randomize weights?

If you forget to randomize weights, or accidentally initialize them all to the same value, common pitfalls include:

• Your loss may not decrease properly, because each neuron in a layer is receiving and computing the same signals. The network cannot learn meaningful feature representations.

• You may see no improvement in training accuracy over random guessing.

• Your gradients might collapse to the same pattern across all neurons, resulting in “dead” updates or updates that do not change from iteration to iteration.

Are there any specialized neural networks that do not require random initialization?

Some models such as certain kernel machines or other “fixed feature” architectures do not require random initialization of weights—because they do not have learnable weights in the typical sense. However, most deep neural networks designed for supervised or unsupervised learning do rely on random weight initialization. Even in networks like reservoir computing or echo state networks, which partially fix internal recurrent weights, there is still a random initialization step for that reservoir.

Therefore, in mainstream deep learning, random initialization remains a fundamental best practice for ensuring that training will break symmetry, drive unique neuron updates, and learn robust features.

---

Below are additional follow-up questions

What happens if we change the random seed every time we train the model? Will that affect reproducibility and performance?

Whenever you train a deep neural network, you rely on a random number generator for various tasks such as weight initialization, shuffling of training data, and data augmentation. By default, if you do not fix the random seed, each run will produce slightly different initial weights and mini-batch orders. These differences can lead to variations in model performance (e.g., accuracy, loss) from run to run. This variability can sometimes be desirable because it may indicate how robust or stable the training process is. However, it can hamper reproducibility if you need to replicate exact results later.

In general, small fluctuations in performance do not necessarily mean the training process is unstable; it might simply mean that you found slightly different local minima for each run. For reproducibility, many practitioners fix the random seed:

import torch
import random
import numpy as np

def set_seed(seed):
    random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    if torch.cuda.is_available():
        torch.cuda.manual_seed_all(seed)

set_seed(42)  # fixed seed

This ensures that each training run initializes weights in exactly the same way (plus identical data shuffling). When you want to explore variability, you can run multiple seeds and report an average result with confidence intervals.

Potential pitfall: • If you rely too heavily on a single random seed, you might overfit to one initialization. A good best practice is to test multiple seeds to gauge average performance. • Some GPU operations are inherently non-deterministic, so even with a fixed seed, perfect reproducibility might be elusive unless you disable certain optimizations.

How does random weight initialization intersect with network depth and the vanishing/exploding gradient problem?

As networks deepen, gradients can become numerically unstable (they might diminish to near zero or explode to very large magnitudes). Proper random initialization can mitigate this by scaling initial weights so that the signals are neither too large nor too small as they propagate forward or backward.

If weights are not scaled correctly, you can encounter:

• Vanishing gradients: Where partial derivatives become so small that the weights in earlier layers barely update.

• Exploding gradients: Where partial derivatives become so large they cause weights to oscillate or diverge.

Xavier (Glorot) initialization and He initialization are designed to keep the variance of signals across layers more stable, significantly reducing these risks. For example, in a very deep network using ReLU activations, He initialization

aims to preserve the variance of the outputs of each layer, preventing them from collapsing to zero or skyrocketing in magnitude.

Potential edge case: • Extremely deep networks with poor initialization can still experience issues. Techniques such as skip connections (as in ResNet architectures) are often introduced to further alleviate vanishing or exploding gradients, in addition to the choice of initialization scheme.

Does random weight initialization help in preventing overfitting?

Random weight initialization itself does not inherently prevent overfitting. Overfitting occurs when a model memorizes training data at the expense of generalization. While random initialization breaks symmetry and allows each neuron to learn distinct features, overfitting is more directly controlled by:

• Regularization techniques (weight decay, dropout, etc.). • Proper dataset size or data augmentation. • Early stopping. • Careful architecture design.

Without these countermeasures, a network can still overfit even with a perfect random initialization scheme. Randomization is critical for breaking symmetry but not sufficient for controlling overfitting.

Potential pitfall: • Relying solely on random initialization and ignoring overfitting signals (like a training loss that decreases steadily while validation loss increases) may result in poor generalization.

Is it possible to exploit structured initialization in some specialized problems rather than purely random initialization?

Yes, in certain specialized problems or architectures, you might use structured initialization. For instance, in networks that incorporate prior knowledge about a domain, such as certain computer vision tasks or signal processing tasks, you may initialize some layers to represent known transformations (e.g., convolutional filters approximating Gabor filters or wavelets). This is often called “smart initialization.”

Potential examples: • Transfer learning: When starting with a pretrained model, you effectively have a “structured initialization” that comes from training on a large dataset (like ImageNet). • Orthogonal initialization: In some RNNs or specialized architectures, orthogonal or identity-based initializations can help maintain signal flow.

However, for most generic deep learning tasks, purely random but properly scaled initialization remains the baseline. The structured approach can be beneficial if there is strong domain-specific motivation to do so.

Could random initialization negatively impact interpretability of model parameters?

Interpretability (the ability to directly understand or interpret what each learned parameter represents) is often more challenging when weights are randomly initialized and learned in a black-box fashion. Even though certain forms of interpretability, like feature visualization or saliency maps, work well to show how the network responds to input stimuli, the initial random seeds add another source of variation. For example, the “concepts” learned by each neuron in a convolutional layer can vary significantly across runs with different random seeds.

However, interpretability challenges are more a feature of modern deep networks in general. Even if you assigned the same initial weights to all neurons (which is obviously detrimental for training quality), interpretability issues would not fundamentally be solved. They stem from the high-dimensional nature of neural network parameters and complex interactions between layers. So while random initialization does add variety, the main interpretability challenges lie deeper in the model’s architecture and training process.

Potential subtlety: • If you are using interpretability tools that rely on analyzing specific neuron weights or activations, the difference in initialization seeds might yield different “named” features in each run. But each run can still learn a valid set of discriminative features.

Does random weight initialization matter as much in large language models (LLMs)?

For large language models with transformers, random initialization is still crucial. Even if these models are often pretrained and then fine-tuned for downstream tasks, the original training of the base architecture begins with carefully chosen random weight distributions (often Xavier or variants thereof). This ensures that each attention head and feed-forward sub-layer starts distinct enough to learn specialized relationships in language.

In large-scale pretraining, you must also pay attention to initialization-facilitated stability:

• Transformers have many layers, multi-head attention blocks, layer normalization, etc. • If initialization is poorly scaled, you might encounter massive gradient instabilities or fail to learn meaningful attention patterns.

Once the LLM is pretrained, fine-tuning typically keeps the same set of weights as the “starting point.” So while randomization is a one-time choice in that sense, it profoundly influences how the entire model eventually learns to represent language.

How do initialization schemes interact with advanced optimization algorithms like Adam, RMSProp, or LAMB?

Even if you use an adaptive optimizer (like Adam), the initial weight distribution still shapes the early gradients. Adaptive optimizers automatically scale the learning rate per parameter dimension, but if all parameters are initialized to the same values, the updates for each parameter may remain identical initially, again failing to break symmetry. So random initialization is essential regardless of whether you use SGD, Adam, RMSProp, or LAMB:

• Adam-based optimizers adapt learning rates based on first and second moments of gradients, but they still rely on the diversity of the gradient signals from different parameters. • LAMB is often used for large-batch training, particularly in large language models. Even in these scenarios, the network requires a diverse set of initial parameters to learn effectively.

Edge case: • In certain specialized architectures or training regimes (e.g., meta-learning or few-shot), there can be custom initialization schemes that are learned from data. Nevertheless, the principle remains: you need some mechanism to ensure parameter diversity.

What if the dataset is very small? Does random initialization matter in that scenario?

If your dataset is extremely small, you can overfit very quickly regardless of how you initialize. Still, random initialization remains necessary to break symmetry among the neurons. However, the training process might require strong regularization or a simpler architecture to avoid overfitting. You might also consider transfer learning (where you start from a pretrained model) rather than training from scratch.

Pitfalls in small data regimes: • Overfitting can occur rapidly, so even if you start randomly, your network might memorize the training set. • If you do not randomize at all, you definitely cannot learn anything beyond a single repeated filter or pattern across neurons. • For very small datasets, you often see more variance in performance from run to run because the data is insufficient to robustly shape parameter updates. Re-running multiple seeds can help you get a more reliable estimate of your true generalization performance.

Can random initialization cause certain layers to “die” or become non-functional?

In principle, if you choose extremely poor initialization values, especially when using activation functions with threshold effects (like ReLU), you risk pushing many neuron outputs into a region of zero activation from which they cannot recover. This is sometimes referred to as the “dying ReLU” problem. A well-chosen random initialization helps ensure that at least early in training, neuron outputs are distributed so that a reasonable fraction of them are active.

Techniques to reduce the likelihood of dying neurons include:

• He initialization (specifically designed for ReLU-based networks). • Leaky ReLU or other activations (ELU, SELU, etc.) that do not zero out negative inputs entirely. • Proper tuning of learning rates and other hyperparameters.

Even with these safeguards, some neurons may become inactive if the gradients push them into regimes of zero activation, but proper initialization plus dynamic activation functions mitigate the problem significantly.

Could constant initialization ever be intentionally used to test hardware or software pipelines?

Yes, but only for debugging. Engineers sometimes intentionally set all weights to zero or some constant to test if the forward pass or backward pass is working as expected in a brand-new software or hardware environment. This helps isolate issues (like memory corruption, incorrect indexing, or floating-point errors) because you remove the unpredictability of randomization and confirm that certain signals match known reference outputs. However, this is not a training configuration meant to produce a useful model. It is purely a debugging or verification step.

Edge case in production environments: • If you see all gradients or outputs as constant during training, it might indicate an unintentional constant initialization or some bug replicating weights incorrectly. Checking initial weight histograms or printing out a few weight values at initialization can help catch such mistakes.

What if I am doing reinforcement learning (RL)? Does random initialization follow the same principles?

In reinforcement learning with deep function approximators, random initialization is just as important for breaking symmetry. Whether you are training a policy network, a value network, or an actor-critic setup, you need to ensure each neuron or parameter has unique initial values. The environment might add another layer of stochasticity (via exploration), but that does not eliminate the need for diverse initial weights.

Pitfalls in RL if you do not randomize properly: • Your policy or value function might fail to learn meaningful distinctions between different states or actions. • If your environment also has strong stochastic components, debugging can become tricky if you do not fix seeds for both the environment and the model.

How can I diagnose if my network’s poor performance might be caused by improper weight initialization?

When diagnosing issues in a neural network, you might suspect improper initialization if:

• The network’s output remains near some constant value no matter the input. • The gradients are all zero or extremely close to zero from the first few iterations onward. • The loss fails to decrease at all after multiple epochs. • Your weight distribution is suspiciously narrow (e.g., all weights are near zero) or suspiciously large, leading to NaN values during forward/backward passes.

To confirm, you can:

• Print or visualize the histogram of your weights and biases before and after initialization. • Check a small forward pass through the network, ensuring the outputs are not all identical or saturating the activations. • Experiment with known, well-tested initialization schemes (e.g., Xavier, He). • Make sure the random seed is set or that you are indeed calling the correct initialization routine rather than some placeholder code that might be zeroing out everything.